The point charges Q and −2Q are placed at some distance apart. If the electirc field at the location of Q is E, the electric field at the location of −2Q will be
(a) 3 E
(b) E/2
(c) E
(d) None of these
The correct Answer is:D
To solve the problem, we need to analyze the electric fields created by the point charges Q and −2Q at their respective locations.
1. Understanding Electric Fields:
The electric field E due to a point charge Q at a distance r is given by the formula:
E=kQr2
where k is Coulomb's constant.
2. Electric Field at the Location of Charge Q:
- The electric field at the location of charge Q (due to charge −2Q) can be calculated as:
E=k(−2Q)r2=−2kQr2
However, since the problem states that the electric field at the location of Q is E, we can denote:
E=−2kQr2
3. Electric Field at the Location of Charge −2Q:
- The electric field at the location of charge −2Q (due to charge Q) is:
E′=kQr2
4. Relating the Electric Fields:
- From the previous step, we have:
E′=kQr2
- Since we know that E=−2kQr2, we can express kQ/r2 in terms of E:
kQ=−E⋅r22
- Substituting this back into the equation for E′:
E′=−E⋅r22r2=−E2
5. Final Result:
- Therefore, the electric field at the location of charge −2Q is:
E′=−E2
Conclusion:
The electric field at the location of charge −2Q is −E2.
The electric field E due to a point charge Q at a distance r is given by the formula:
E=kQr2
where k is Coulomb's constant.
- The electric field at the location of charge Q (due to charge −2Q) can be calculated as:
E=k(−2Q)r2=−2kQr2
However, since the problem states that the electric field at the location of Q is E, we can denote:
E=−2kQr2
- The electric field at the location of charge −2Q (due to charge Q) is:
E′=kQr2
- From the previous step, we have:
E′=kQr2
- Since we know that E=−2kQr2, we can express kQ/r2 in terms of E:
kQ=−E⋅r22
- Substituting this back into the equation for E′:
E′=−E⋅r22r2=−E2
- Therefore, the electric field at the location of charge −2Q is:
E′=−E2
The electric field at the location of charge −2Q is −E2.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.5
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Two point charges Q and -3Q are placed at some distance apart. If the electric field at the location of Q is →E, the field at the location of - 3Q is
View SolutionTwo point charges +Q and -Q are separated by a certain distance. The resultant electric field is parallel to the line joining the charges at the points
View SolutionCharges Q and -2Q are placed at some distance. The locus of points in the plane of the charges where the potential is zero will be :
View SolutionTwo charges 4q and q are placed 30 cm. apart. At what point the value of electric field will be zero
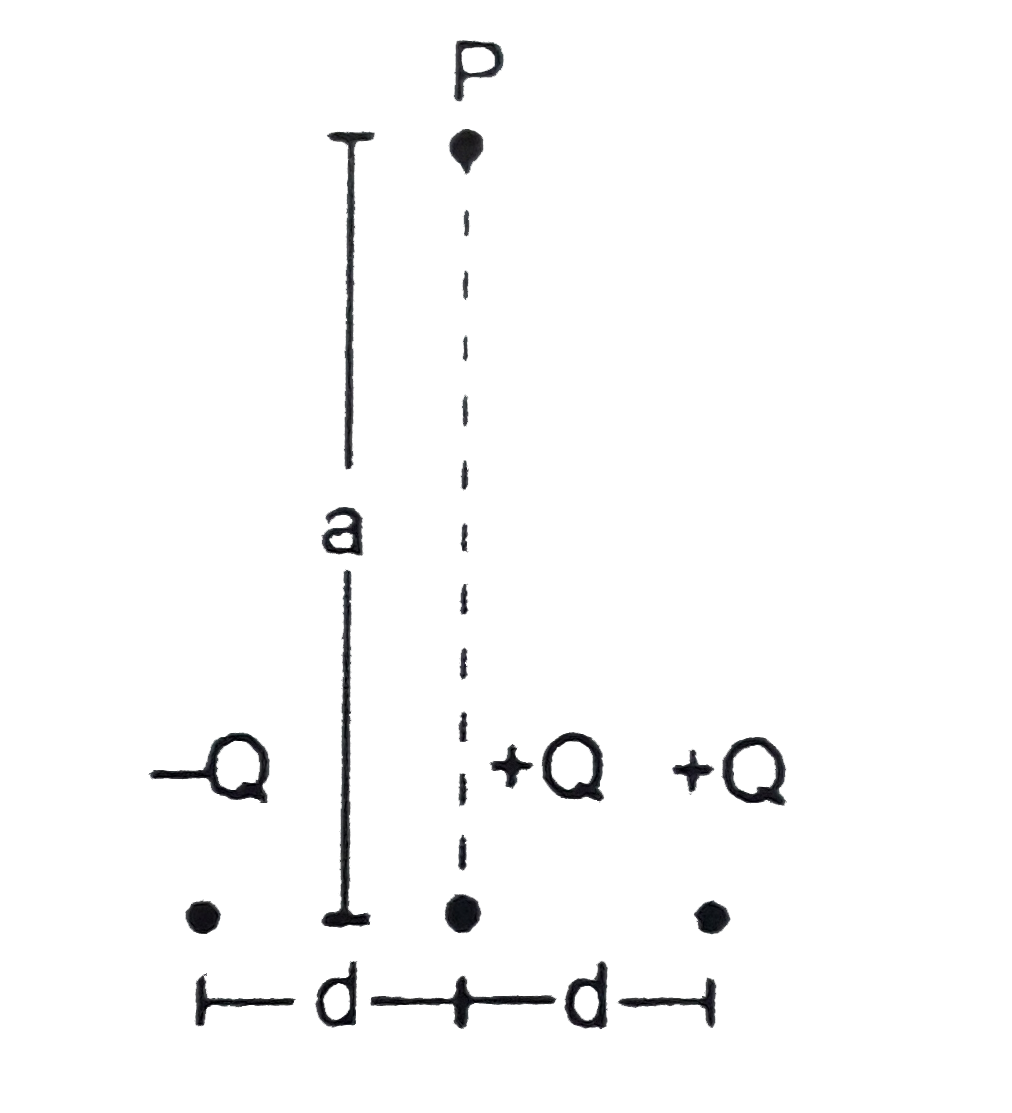
View SolutionThree point charges -Q, Q and Q are placed on a straight line with distance d between charges as shown. Find the magnitude of the electric field at the point P in the configuration shown which is at a distance a from middle charge Q in the system provided that a>>d. Take 2Qd=p.
View SolutionTwo point charges q and -q are separated by a distance 2a. Evaluate the flux of the electric field strength vector across a circle of radius R.

View SolutionTwo point charges +q and −q are placed a distance x apart. A third charge is so placed that at the three charges are in equilibrium. Then
View SolutionTwo point charges +8q and −2q are located at x=0 and x=L respectively. The location of a point on the x axis at which the net electric field due to these two point charges is zero is
View SolutionTwo point charges 2q and 8q are placed at a distance r apart. Where should a third charge −q be placed between them so that the electrical potential energy of the system is a minimum
View SolutionCharge 2Q and −Q are placed as shown in figure. The point at which electric field intensity is zero will be somewhere

View Solution
