The electric charges are distributed in a small volume. The flux of the electric field through a spherica surface of radius 10 cm surrounding the total charge is 20V−m. The flux over a concentric sphere of radius 20 cm will be
20 Vm
10 Vm
40 Vm
5 Vm
The correct Answer is:A
Step by step video & image solution for The electric charges are distributed in a small volume. The flux of the electric field through a spherica surface of radius 10 cm surrounding the total charge is 20 V - m. The flux over a concentric sphere of radius 20 cm will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason15videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns5videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.520videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
Electric charge are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10cm surrounding the total charge is 25 V m. The flux over a concentric sphere of radius 20 cm will be
View SolutionThe flux of electric field through the circular region of radius r as shown in the figure is
_PHY_E05_291_Q01.png)
View SolutionFind the flux due to the electric field through the curved surface (R is radius of curvature)
View SolutionA charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaced of the cube.
View SolutionFigure shown below is a distribution of charges. The flux of electric field due to these charges through the surface S is
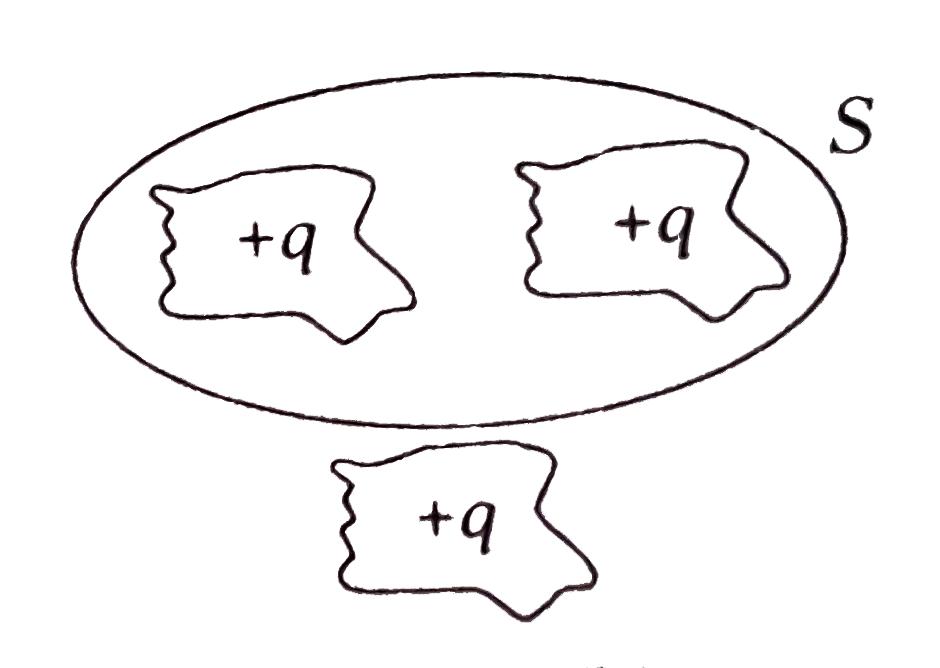
View SolutionFigure shown below is a distribution of charges. The flux of electric field due to these charges through the surface S is
View SolutionA capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the capacitor is
View SolutionA charge q is placed at the centre of the open end of a cylindrical vessel . The flux of the electric field through the surface of the vessel is
View SolutionThe magnitude of the electric field on the surface of a sphere of radius r having a uniform surface charge density σ is
View SolutionFind the flux of the electric field through each of the five surfaces of the inclined plane as shown in figure. What is the total flux through the entire closed surface?
View Solution