The position of a particle moving rectilinearly is given by x=t3−3t2−10. Find the distance travelled by the particle in the first 4 seconds starting from t=0.
24 unit
36 unit
15 unit
50 unit
The correct Answer is:A
x=t3−3t2−10
v=dxdt=3t2−6t
Now, v=0 gives
t=0 and t=2sec
Velocity will becomes zero at t=2sec., so particle will change direction after t=2sec.
At t=0
x(0sec)=−10
At t=2sec
x(2sec)=23−3(2)2−10=8−12−10=−14
At t=4sec
x(4sec)=43−3(4)2−10
=64−48−10=6
Distance travelled =x1+x2
=|−14−(−10)|+|6−(−14)|=4+20=24
Distance Travelled =24 units.
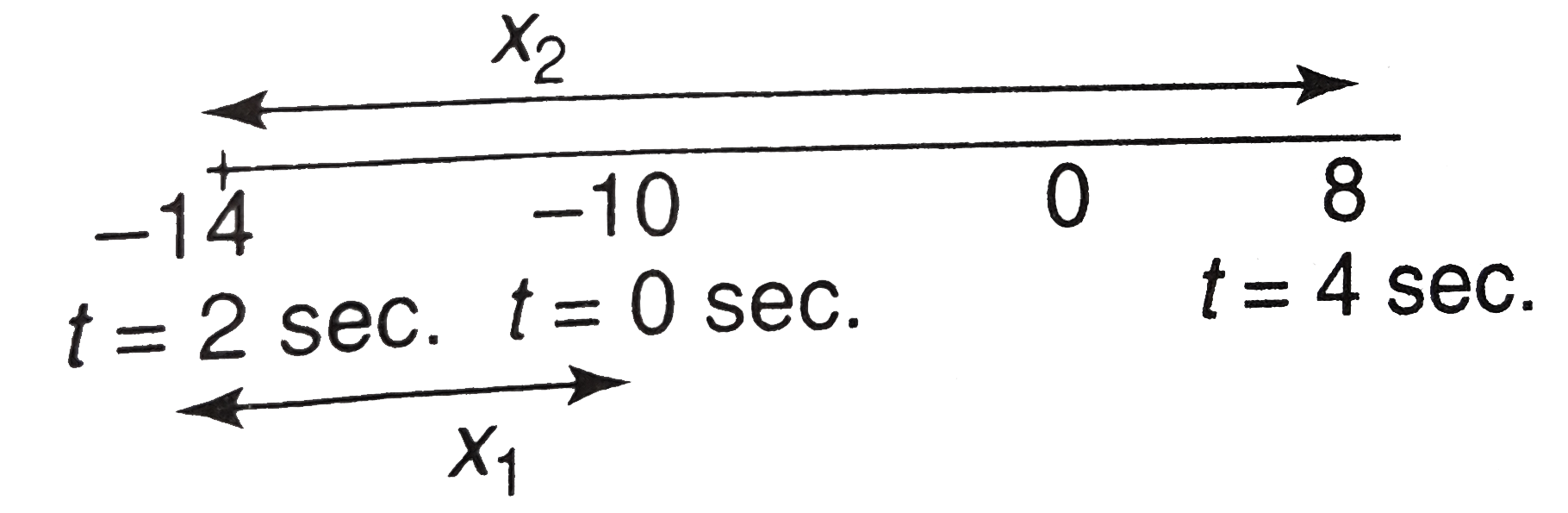 .
.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - AIIMS Questions20videos
GENERAL KINEMATICS AND MOTION IN ONE DIMENSION
- BOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Chapter Test29videos
FLUID MECHANICS
- BOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test29videos
GRAVITATION
Similar Questions
The position of a particle along x-axis at time t is given by x=1−t+t2. The distance travelled by the particle (in 'm') in first 2 seconds is 's'. Fill '2s' in OME sheet.
View Solutionx−t equation of a particle in SHM is
x=(4cm)cos(π2t)
Here ,t is in seconds. Find the distance travelled by the particle in first three seconds.View Solution
Knowledge Check
- Question 1 - Select One
The position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
A1 mB2 mC2.5 mD3 m - Question 2 - Select One
Position of a particle moving along x-axis is given by x=2+8t−4t2. The distance travelled by the particle from t=0 to t=2 is:-
A0B8C12D16 - Question 3 - Select One
If S=3t3+9t2+2t+7 , then distance travelled by the particle during the first second of its motion is
A7 unitsB21 unitsC14 unitsD28 units
Position vector of a particle moving in space is given by :
→r=3sintˆi+3costˆj+4tˆk
Distance travelled by the particle in 2s is :View SolutionThe position x of a particle varies with time t as x=6+12t−2t2 where x is in metre and t is in seconds. The distance travelled by the particle in first five seconds is
View SolutionThe position of a particle moving in a string line is given by
x=3t3−18t2+36t
Here, x is in m and t in second . ThenView SolutionThe displacement of a particle is moving by x=(t−2)2 where x is in metres and t in second. The distance covered by the particle in first 4 seconds is.
View SolutionIf S=13t3−4t2+12t, then distance travelled by the particle before it first comes to rest is
View Solution

