The position of centre of mass of system of particles at any moment does not depend on.
masses of the particles
internal forces on the particles
position of the particles
relative distance between the particles
The correct Answer is:B
To solve the question about the position of the center of mass of a system of particles and what it does not depend on, we can follow these steps:
1. Understanding the Center of Mass:
The center of mass (COM) of a system of particles is a point that represents the average position of the mass distribution in the system. It is calculated using the formula:
→Rcm=m1→r1+m2→r2+m3→r3+…+mn→rnm1+m2+m3+…+mn
where mi is the mass of the ith particle and →ri is its position vector.
2. Analyzing the Dependencies:
- Masses of the Particles: The position of the center of mass depends on the masses of the particles, as seen in the numerator of the COM formula.
- Position of the Particles: The position vectors →ri also directly influence the center of mass, as they are part of the calculation.
- Relative Distance Between the Particles: The relative distances between particles affect the position of the center of mass since they determine how the masses are distributed in space.
- Internal Forces on the Particles: Internal forces (forces that particles exert on each other) do not affect the position of the center of mass. The center of mass is determined solely by the masses and their positions, not by the forces acting between them.
3. Conclusion:
Based on the analysis above, we can conclude that the position of the center of mass does not depend on the internal forces acting on the particles. Therefore, the correct answer to the question is that the position of the center of mass does not depend on internal forces on the particles.
Final Answer:
The position of the center of mass of a system of particles does not depend on internal forces on the particles.
---
The center of mass (COM) of a system of particles is a point that represents the average position of the mass distribution in the system. It is calculated using the formula:
→Rcm=m1→r1+m2→r2+m3→r3+…+mn→rnm1+m2+m3+…+mn
where mi is the mass of the ith particle and →ri is its position vector.
- Masses of the Particles: The position of the center of mass depends on the masses of the particles, as seen in the numerator of the COM formula.
- Position of the Particles: The position vectors →ri also directly influence the center of mass, as they are part of the calculation.
- Relative Distance Between the Particles: The relative distances between particles affect the position of the center of mass since they determine how the masses are distributed in space.
- Internal Forces on the Particles: Internal forces (forces that particles exert on each other) do not affect the position of the center of mass. The center of mass is determined solely by the masses and their positions, not by the forces acting between them.
Based on the analysis above, we can conclude that the position of the center of mass does not depend on the internal forces acting on the particles. Therefore, the correct answer to the question is that the position of the center of mass does not depend on internal forces on the particles.
The position of the center of mass of a system of particles does not depend on internal forces on the particles.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Taking it together
73 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
Knowledge Check
Centre of mass of three particles of masses 1kg,2kgand3kg lies at the point (1,2,3) and centre of mass of another system of particles 3kgand2kg lies at the point (−1,3,−2). Where should we put a particle of mass 5kg so that the centre of mass of entire system lies at the centre of mass of first system ?
A(0, 0, 0)B(1, 3, 2)C(-1, 2, 3)D(3, 1, 8)
The centre of mass of a system of particles is at the origin. It follows that:
View SolutionCalculate centre of mass of the system
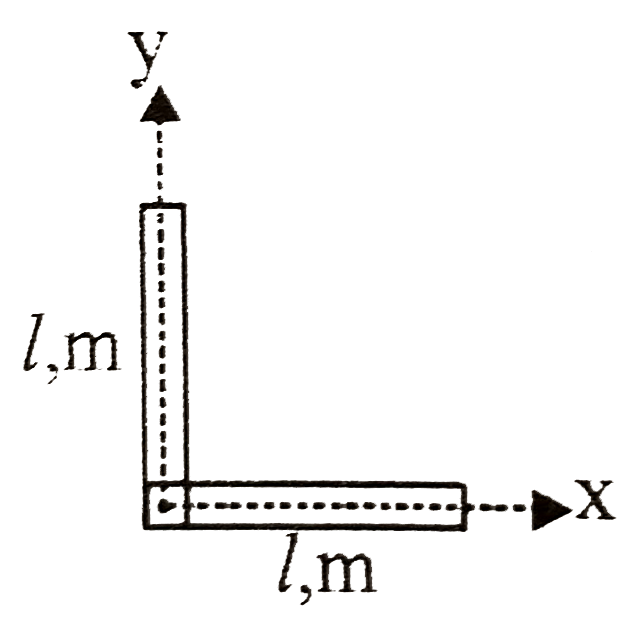
View SolutionThe position co-ordinates of the centre of mass of a system of three particles of equal masses which are placed on the verctices of an equilateral triangle of a side a are shown. Locate centre mass?

View SolutionThe coordinates of the centre of mass of a system of three particles of mass 1g,2g and 3g are (2,2,2). Where should a fourth particle of mass 4 g be positioned so that the centre of mass of the four particle system is at the origin of the three-dimensional coordinate system ?
View SolutionThe moment of inertia of a body does not depend on
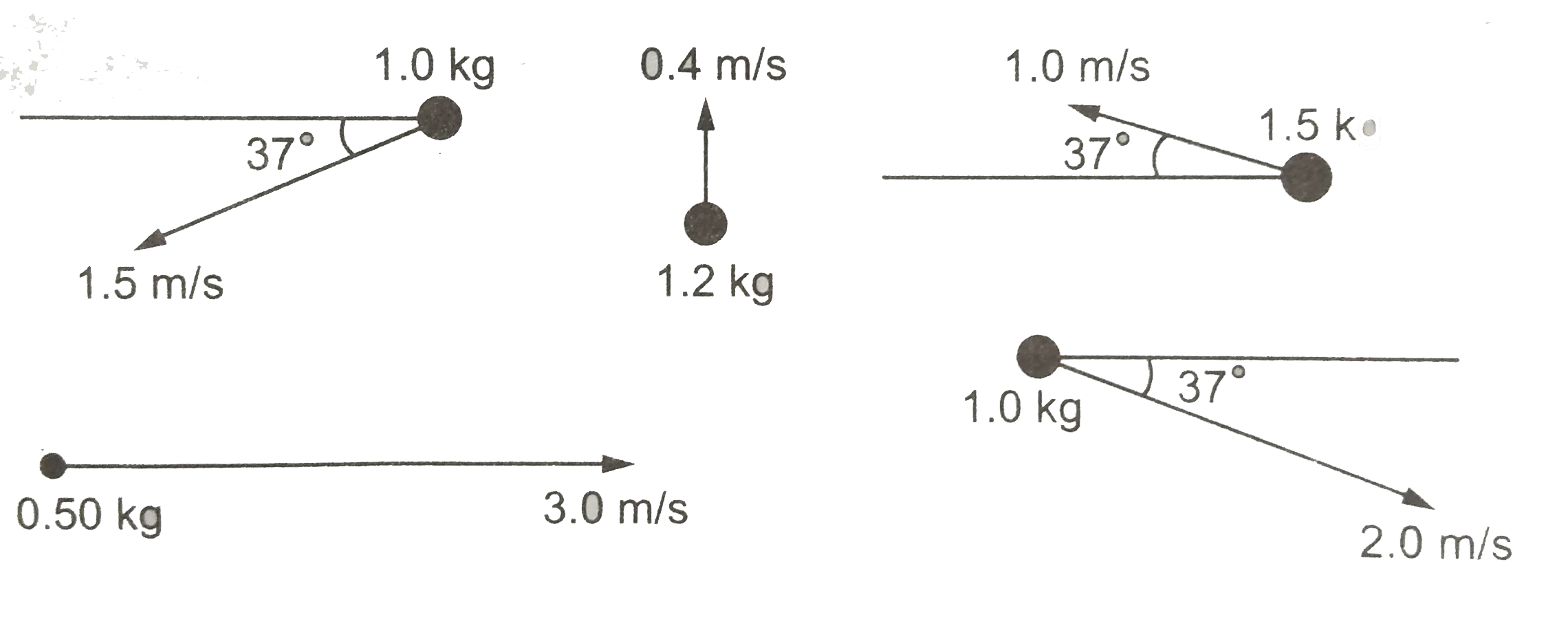
View SolutionCalculate the velocity of the centre of mss of the system of particles shown in figure.
View SolutionFind the position of centre of mass of the section shown in figure

View Solution
