The potential difference between the terminals of a battery of emf 6.0V and internal resistance1(Ω)drops to 5.8 V when connected across an external resistor. Find the resistance of the external resistor.
To solve the problem step-by-step, we will follow these steps:
Step 1: Understand the given information
We have a battery with:
- EMF (E) = 6.0 V
- Internal resistance (r) = 1 Ω
- Terminal voltage (V) when connected to an external resistor = 5.8 V
Step 2: Apply Kirchhoff's Voltage Law (KVL)
According to KVL, the potential difference across the external resistor plus the potential drop across the internal resistance should equal the EMF of the battery.
The equation can be written as:
E=V+I⋅r
Where:
- I is the current flowing through the circuit.
Step 3: Rearrange the equation to find the current (I)
From the KVL equation:
I=E−Vr
Substituting the known values:
- E = 6.0 V
- V = 5.8 V
- r = 1 Ω
We get:
I=6.0V−5.8V1Ω
I=0.2V1Ω=0.2A
Step 4: Find the external resistance (R)
Now we can use the terminal voltage (V) and the current (I) to find the external resistance (R) using Ohm's Law:
V=I⋅R
Rearranging gives us:
R=VI
Substituting the known values:
- V = 5.8 V
- I = 0.2 A
We get:
R=5.8V0.2A
R=29Ω
Final Answer
The resistance of the external resistor is 29 Ω.
---
We have a battery with:
- EMF (E) = 6.0 V
- Internal resistance (r) = 1 Ω
- Terminal voltage (V) when connected to an external resistor = 5.8 V
According to KVL, the potential difference across the external resistor plus the potential drop across the internal resistance should equal the EMF of the battery.
E=V+I⋅r
- I is the current flowing through the circuit.
From the KVL equation:
I=E−Vr
- E = 6.0 V
- V = 5.8 V
- r = 1 Ω
I=6.0V−5.8V1Ω
I=0.2V1Ω=0.2A
Now we can use the terminal voltage (V) and the current (I) to find the external resistance (R) using Ohm's Law:
V=I⋅R
Rearranging gives us:
R=VI
- V = 5.8 V
- I = 0.2 A
R=5.8V0.2A
R=29Ω
The resistance of the external resistor is 29 Ω.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer
17 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 2
9 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
The potential difference across the terminals of a battery of emf12V and internal resistance 2Ω drops to 10V when it is connected to a silver voltameter. Find the silver deposited at the cathode in half an hour. Atomic weight of silver is 107.9gmol−1.
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionA battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
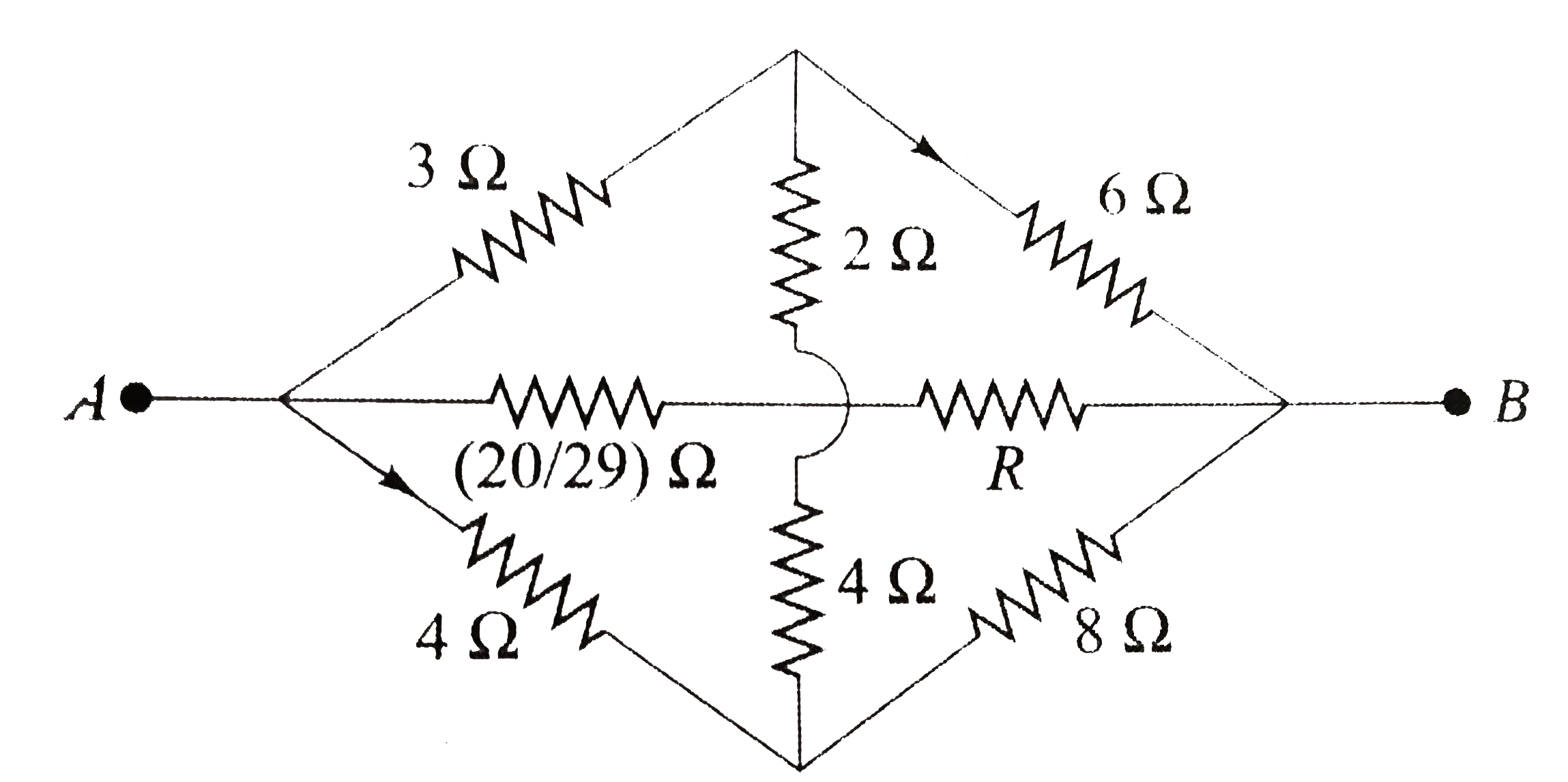 .
.
View SolutionA car battery of emf 12V and internal resistance 0.05ω receives a current of 60 A from an external source, then the terminal potential difference of the battery is
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 6 Ω resistor.
View SolutionA battery of emf 2.0V and internal resistance 0.10Ω is being charged with a current of 5.0A. Find the potential difference between the terminals of the battery?
View SolutionA capacitor of capacitance 1μF is connected in parallel with a resistance 10Ω and the combination is connected across the terminals of a battery of EMF 50 V and internal resistance 1Ω. The potential difference across the capacitor at steady state is (in Volt)
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 3 Ω resistor,
View SolutionTwo cells having emf's of 10 V and 8 V, and internal resistance of 1Ω(each) are connected as shown with an external resistance of 8Ω Find the current flowing through the circuit.
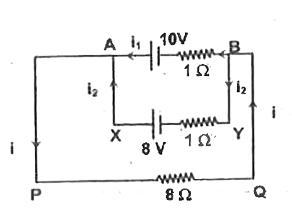
View Solution
