The potential energy function for a particle executing linear simple harmonic motion is given by V(x)=kx22 where k is the force constant of the oscillator . For k=0.5Nm−1 , the graph of V(x) versus x is shown in figure . Show that a particle of total energy 1 J movng under this potential must 'turn back ' when it reaches x=±2m .
 Solution in Gujrati
Solution in Gujrati
Total energy of a simple harmonic oscillator ,
E=K+V
1=12mv2+12kx2 …(1)
When simple harmonic oscillator turn back , at this time its speed or velocity will be zero .
v = 0
∴1=0+12(0.5)x2 [∴From equation (1)]
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - B Numericals (Numerical From .DARPAN. Based On Textbook)
15 Videos
- WORK, ENERGY AND POWER BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - C Objective Questions (VSQs)
52 Videos
- WORK, ENERGY AND POWER BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - B Numericals (Numerical From Textual Illustration)
29 Videos
- WAVESBOOK - KUMAR PRAKASHANCHAPTER - WAVESEXERCISE - SECTION-F (Questions From Module) (Sample questions for preparation of competitive exams)
23 Videos
Similar Questions
A body while being acted upon by a force →F(x)=(3x2−2x+7)ˆi N gets displaced from x = 0 to x = 10 m in the direction of X -axis .Find the work done [∫xndx=xn+1n+1]
View SolutionIf →A=2ˆi−2ˆjand→B=2ˆk then →A.→B……
View SolutionFind the angle between force →F=(3ˆi+4ˆj−5ˆk) unit and displacement →d=(5ˆi+4ˆj+3ˆk) unit , Also find the projection of F on d .
View SolutionIn a standing wave formed by two atoms separated by 1.21Å, there are 3 nodes and 2 antinodes. Find its wavelength.
View SolutionThe potential energy function for a particle executing simple harmonic motion is given by V(x)=(1)/(2)kx^(2) , where k is the force constant of the oscillatore. For k=(1)/(2)Nm^(-1) , show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=+-2m.
View SolutionA particle is executing simple harmonic motion in a conservative force field. The total energy of simple harmonic motion is given by E=ax2+bv2where ‘x’ is the displacement from mean position x = 0 and v is the velocity of the particle at x then choose the INCORRECT statements.{Potential energy at mean position is assumed to be zero}
View SolutionThe potential energy of a particle with displacement X is U(X). The motion is simple harmonic, when (K is a positive constant)
View SolutionThe potential energy function for a particle executing linear SHM is given by V(x)=12kx2 where k is the force constant of the oscillator. For k=0.5Nm−1, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches x=±xm.if V and K indicate the potential energy and kinetic energy respectively of the particle at x=+xm,then which of the following is correct?
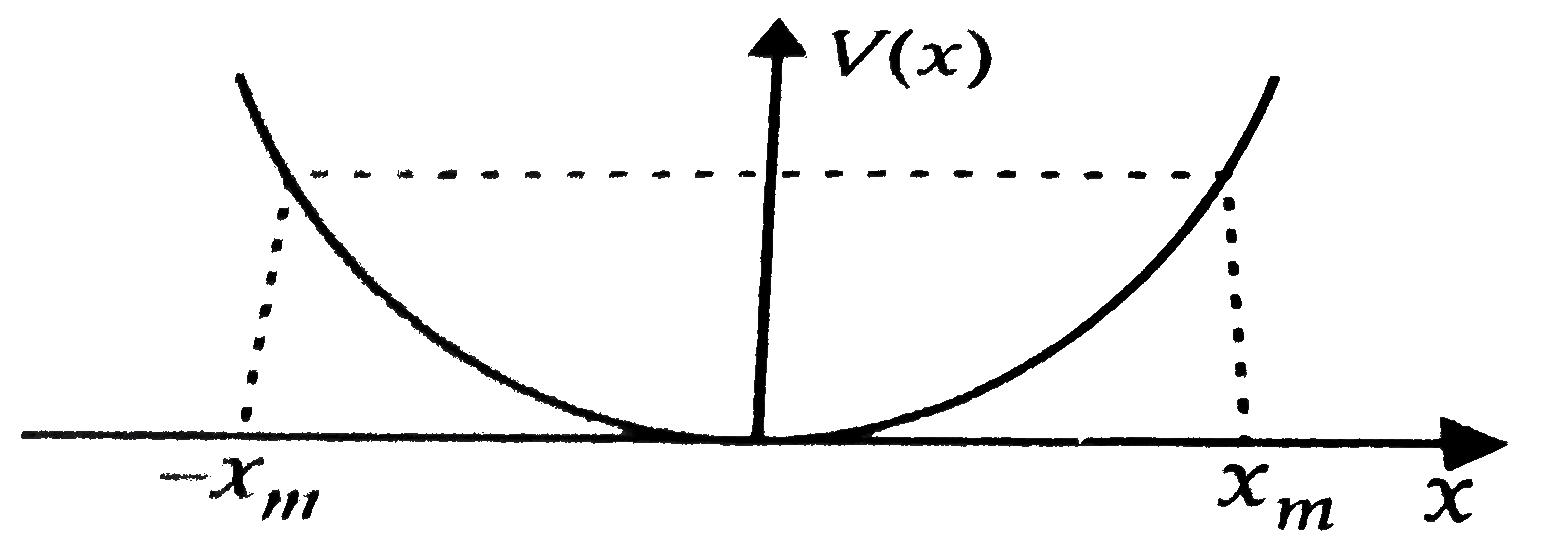
View Solutionरेखीय सरल आवर्त गति कर रहे किसी कण का स्थितिज ऊर्जा फलन V(x)12kx2 है, जहाँ k दोलन का बल नियतांक है। k=0।5Nm−1 के लिए V (x ) व x के मध्य ग्राफ चित्र में दिखाया गया है। यह दिखाइए की इस विभव के अंतर्गत गतिमान कुल 1 J ऊर्जा wale कण को अवश्य ही वापिस आना' चाहिए , अब यह x=±2 मीटर पर पहुँचता है।

View Solutionरेखीय सरल आवर्त गति कर रहे किसी कण का स्थितिज ऊर्जा फलन U(x)=kx2/2 है, जहाँ k दोलक का बल नियतांक है । k=0.5Nm−1 के लिए U(x) व x के मध्य ग्राफ चित्र में दिखाया गया है । यह दिखाइए कि इस विभव के अंतर्गत गतिमान कुल 1J ऊर्जा वाले कण को अवश्य ही 'वापिस आना' चाहिए जब यह x=±2m पर पहुँचता है ।
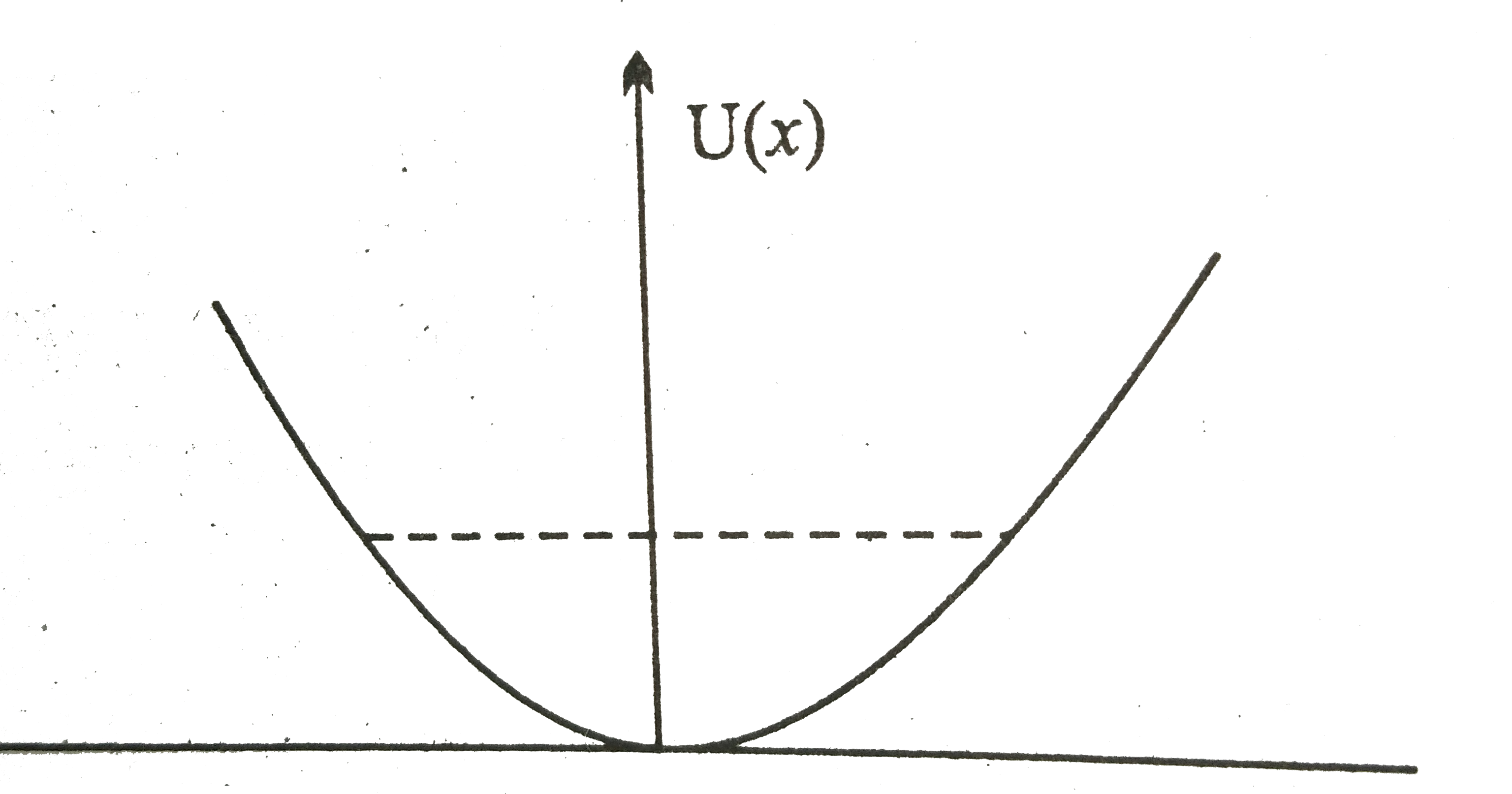
View SolutionThe potential energy function for a particle executing linear simple harmonic motion is given by V(x)= kx^(2)"/"2 , where k is the force constant of the oscillator. For k= 0.5 Nm^(1) , the graph of V(x) versus x is shown in Fig. 6. 12. Show that a particle of total energy 1 J moving under this potential must 'turn back' when it reaches x= pm 2m .
View SolutionThe potential energy function for a particle executing simple harmonic motion is given by V(x)=12kx2, where k is the force constant of the oscillatore. For k=12Nm−1, show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=±2m.
View Solutionसरल रेखीय गति कर रहे किसी कण के लिए स्थितिज ऊर्जा फलन को V(x)=12kx2 के द्वारा निरूपित किया जाता है, जहाँ दोलित्र का बल गुणांक है। k=0.5Nm−1 के लिए, V(x) बनाम x के आरेख को चित्र में दर्शाया गया है। कुल ऊर्जा E का कण उस समय वापस हो जाता है जब यह x=±xm पर पहुँचता है। यदि x=±xm पर किसी कण की स्थितिज व गतिज ऊर्जा को क्रमश: V व K के द्वारा दर्शाया जाता है, तब निम्न में से कौन-सा सही है?
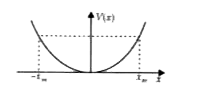
View SolutionThe potential energy function for a particle executing simple harmonic motion is given by V(x)=12kx2, where k is the force constant of the oscillatore. For k=12Nm−1, show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=±2m.
View SolutionThe potential energy function for a particle executing linear simple harmonic motion is given U(x)=1/2kx^(2) , where k is the force constant of the oscillator. For k=0.5 Nm^(-1) , the graph of U(x) on Y-axis x is shown figure. The particle has total energy 1J. Moving this potential it turns back when it reaches x=+- _________m
View Solution