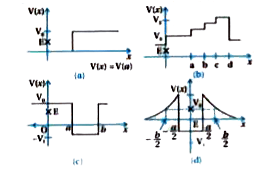
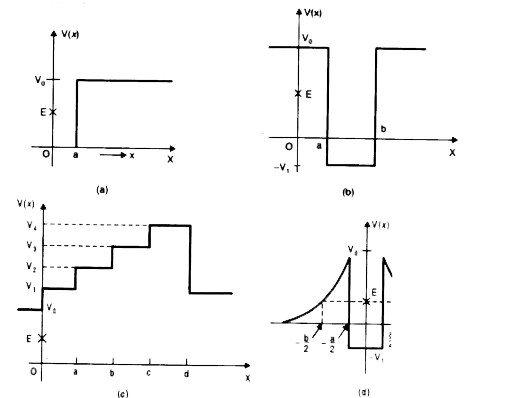
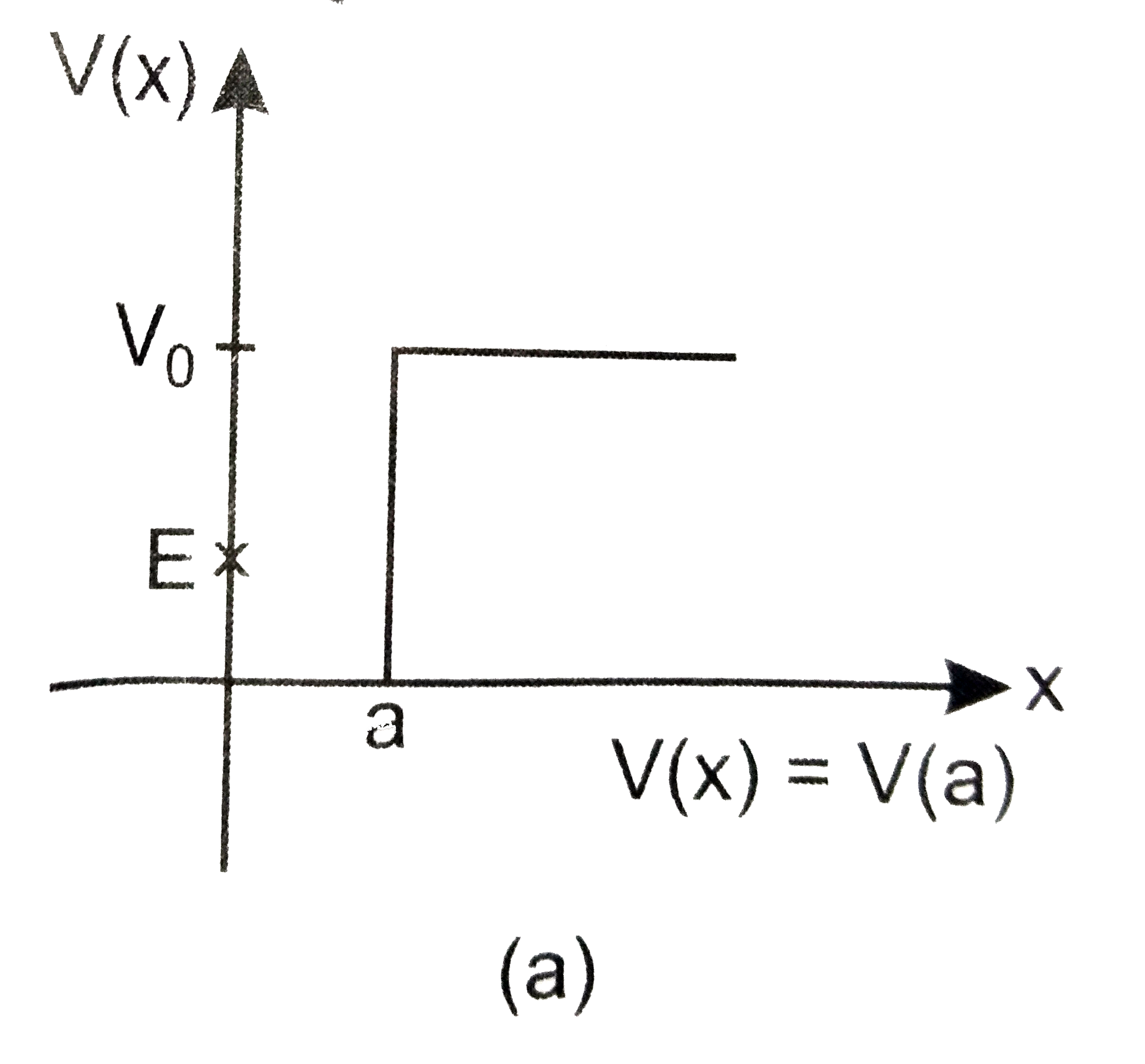
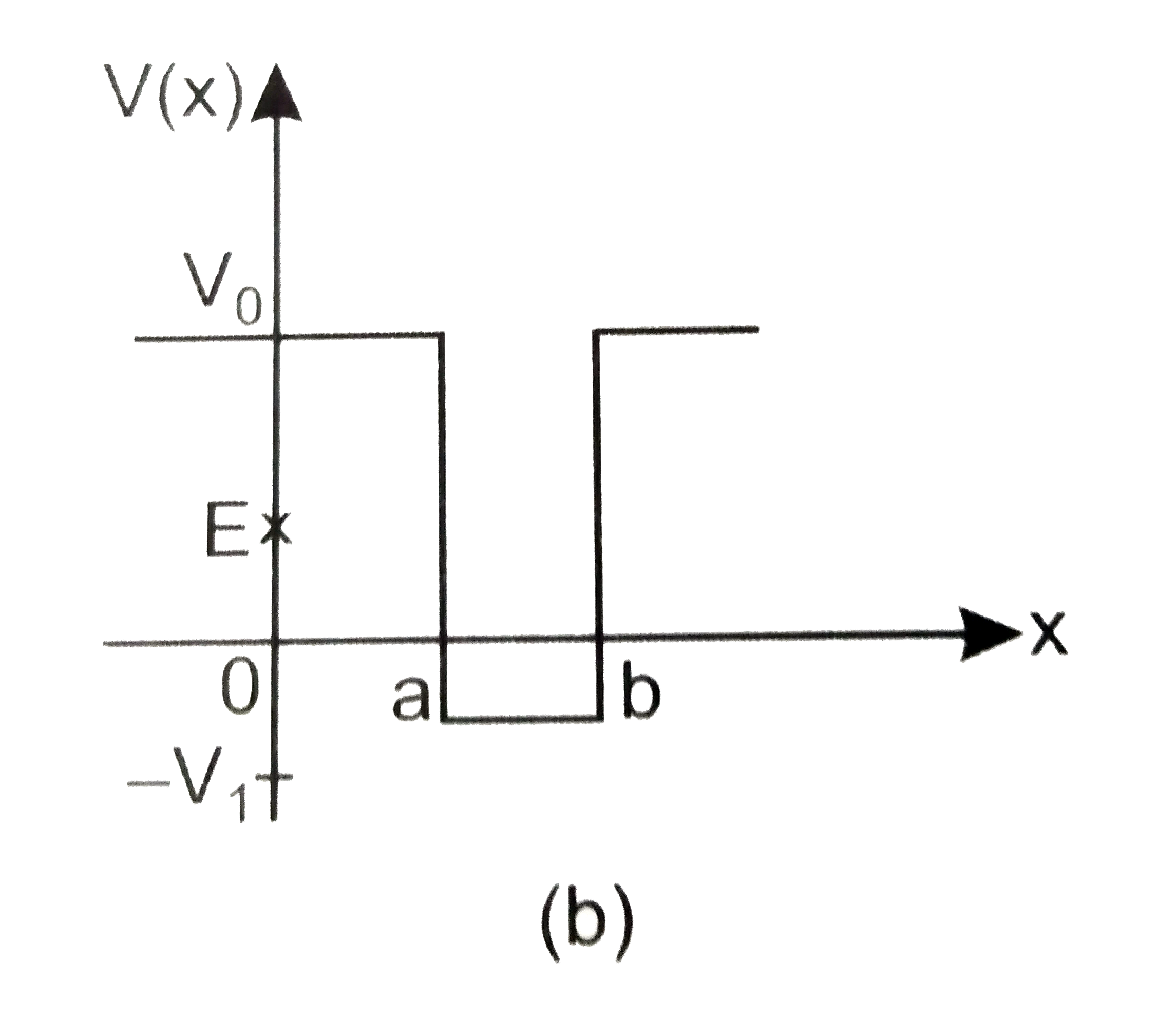
Given in figure are examples of some potential energy functions in one dimension. The total energy of the aprticle is indicated by a cross on the ordinate axis . In each case , specify the regions ,if any , in which the particle cannot be found for the given energy .Also , indicate the minimum total energy the particle must have in each case . Think of simple physical contexts for which these potential energy shapes are relvant .
 Solution in Gujrati
Solution in Gujrati
We know that total energy ,
where V = potential energy ,
K = kinetic energy
and kinetic energy (K) can never be negative If K is negative , the object cannot exist in the region .
(a) In the region between x = 0 and x = a potential energy is zero . So , kinetic energy is positive .In the region the potential energy has a value greater than E . So, kinetic energy has a value greater than E . So kinetic energy will be negative in this region . Thus , the particle cannot be present in the region .the minimum total energy that the particle can have in this case is zero .
(b) In graph (b) potentail energy the total energy and hence kinetic energy would be negative . Thus , object cannot be present in any region of the graph .
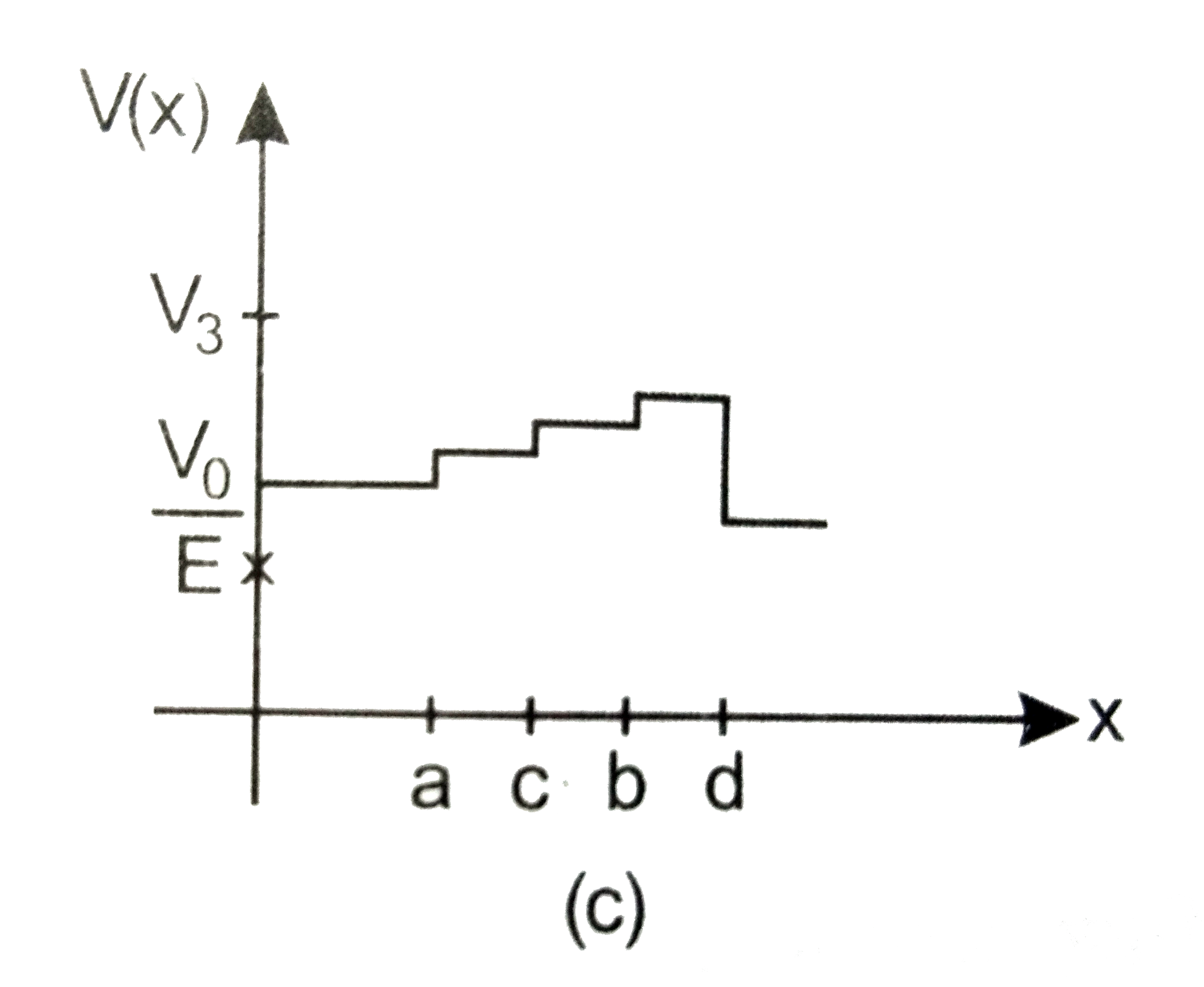
(c ) Here x = 0 to x = 0 and the potential energy is more than total energy , so kinetic energy is negative . the particle cannot exist in these portions .
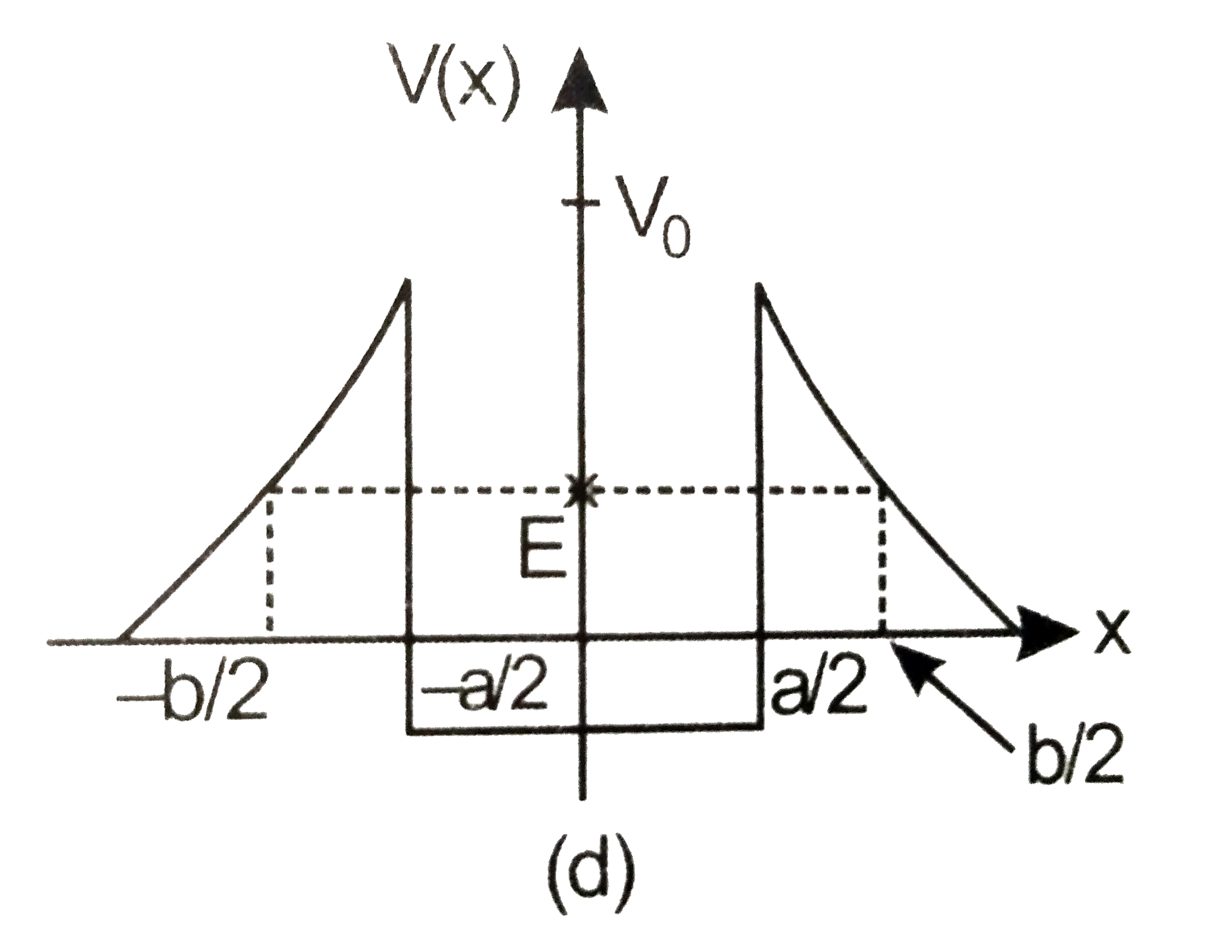
(d) The object cannot exist in the region between .Because in this region potential energy total energy .
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - B Numericals (Numerical From .DARPAN. Based On Textbook)15videos
WORK, ENERGY AND POWER
- BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - C Objective Questions (VSQs)52videos
WORK, ENERGY AND POWER
- BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - B Numericals (Numerical From Textual Illustration)29videos
WORK, ENERGY AND POWER
- BOOK - KUMAR PRAKASHANCHAPTER - WAVESEXERCISE - SECTION-F (Questions From Module) (Sample questions for preparation of competitive exams)23videos
WAVES
Similar Questions
A body while being acted upon by a force →F(x)=(3x2−2x+7)ˆi N gets displaced from x = 0 to x = 10 m in the direction of X -axis .Find the work done [∫xndx=xn+1n+1]
20:15View SolutionIf →A=2ˆi−2ˆjand→B=2ˆk then →A.→B……
01:30View SolutionFind the angle between force →F=(3ˆi+4ˆj−5ˆk) unit and displacement →d=(5ˆi+4ˆj+3ˆk) unit , Also find the projection of F on d .
20:15View SolutionIn a standing wave formed by two atoms separated by 1.21Å, there are 3 nodes and 2 antinodes. Find its wavelength.
07:51View SolutionGiven in fig are examples of some potential energy functions in one dimension. The total enrgy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
 02:04View Solution
02:04View SolutionA particle with total energy E moves in one direction in a region where, the potential energy is U The acceleration of the particle is zero, where,
04:12View SolutionGiven in fig are examples of some potential energy functions in one dimension. The total enrgy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
03:35View Solutionचित्र में कुछ एकविमीय स्थितिज ऊर्जा-फलानो के उदहारण दिये गये हैं। कण की कुल ऊर्जा कोटि-अक्ष पर क्रॉस द्वारा निर्देशित की गई है। प्रत्येक स्थिति में, कोई ऐसे क्षेत्र बताइए,यदि कोई है तो, जिनमे दी गई ऊर्जा के लिए, कण को नहीं पाया जा सकता है। इसके अतिरिक्त, कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिए। कुछ ऐसे भौतिक संदर्भो के विषय में सोचिए जिनके लिए ये स्थितिज ऊर्जा आकृतियाँ प्रासंगिक हो।
 04:55View Solution
04:55View Solutionचित्र 6.11 में कुछ एकविमीय स्थितिज ऊर्जा - फलनो के उदाहरण दिए गए है। कण की कुल ऊर्जा कोटि - अक्ष पर क्रॉस द्वारा निर्देशित की गए है । प्रत्येक स्थिति में, कोई ऐसे क्षेत्र बताइए, यदि कोई है तो, जिनमें दी गई ऊर्जा के लिए, कण को नहीं पाया जा सकता। इसके अतिरिक्त, कण की कुल न्यूतम ऊर्जा भी निर्देशित कीजिए। कुछ ऐसे भोतिक संदर्भो के विषय में सोचिए जिनके लिए ये स्थितिज ऊर्जा आकृतिया प्रासंगिक हो।
 05:52View Solution
05:52View Solutionचित्र में कुछ एकविमीय स्थितिज ऊर्जा - फलनों के उदाहरण दिए गए हैं । कण की कुल ऊर्जा कोटि - अक्ष पर क्रॉस द्वारा निर्देशित की गई है । प्रत्येक स्थिति में, कोई ऐसे क्षेत्र बताइए, यदि कोई हैं तो, जिनमें दी गई ऊर्जा के लिए, कण को नहीं पाया जा सकता । इसके अतिरिक्त, कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिए । कुछ ऐसे भौतिक संदर्भो के विषय में सोचिए जिनके लिए ये स्थितिज ऊर्जा आकृतियाँ प्रासंगिक हों ।
(a)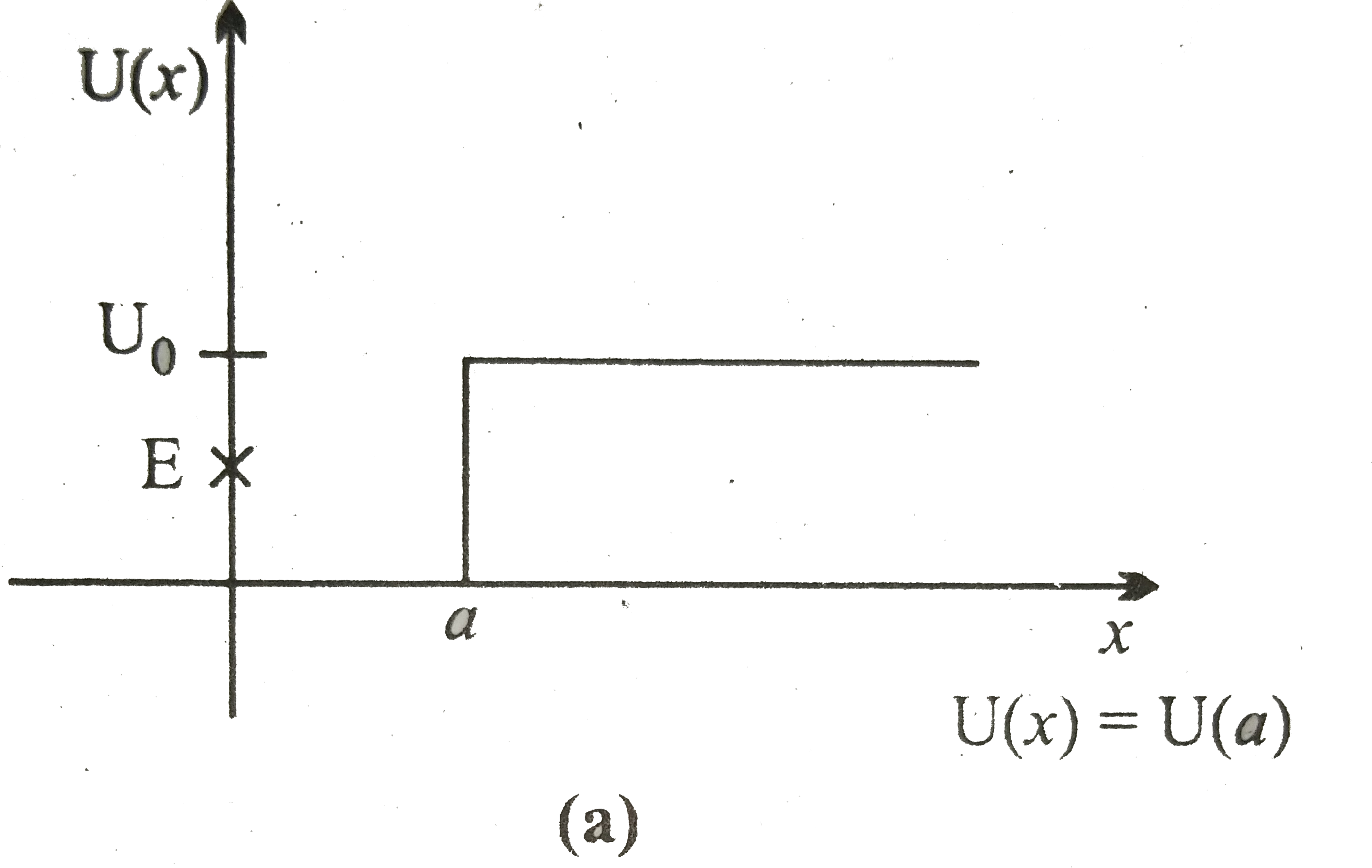 02:28View Solution
02:28View Solutionचित्र में कुछ एकविमीय स्थितिज ऊर्जा - फलनों के उदाहरण दिए गए हैं । कण की कुल ऊर्जा कोटि - अक्ष पर क्रॉस द्वारा निर्देशित की गई है । प्रत्येक स्थिति में, कोई ऐसे क्षेत्र बताइए, यदि कोई हैं तो, जिनमें दी गई ऊर्जा के लिए, कण को नहीं पाया जा सकता । इसके अतिरिक्त, कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिए । कुछ ऐसे भौतिक संदर्भो के विषय में सोचिए जिनके लिए ये स्थितिज ऊर्जा आकृतियाँ प्रासंगिक हों ।
(b)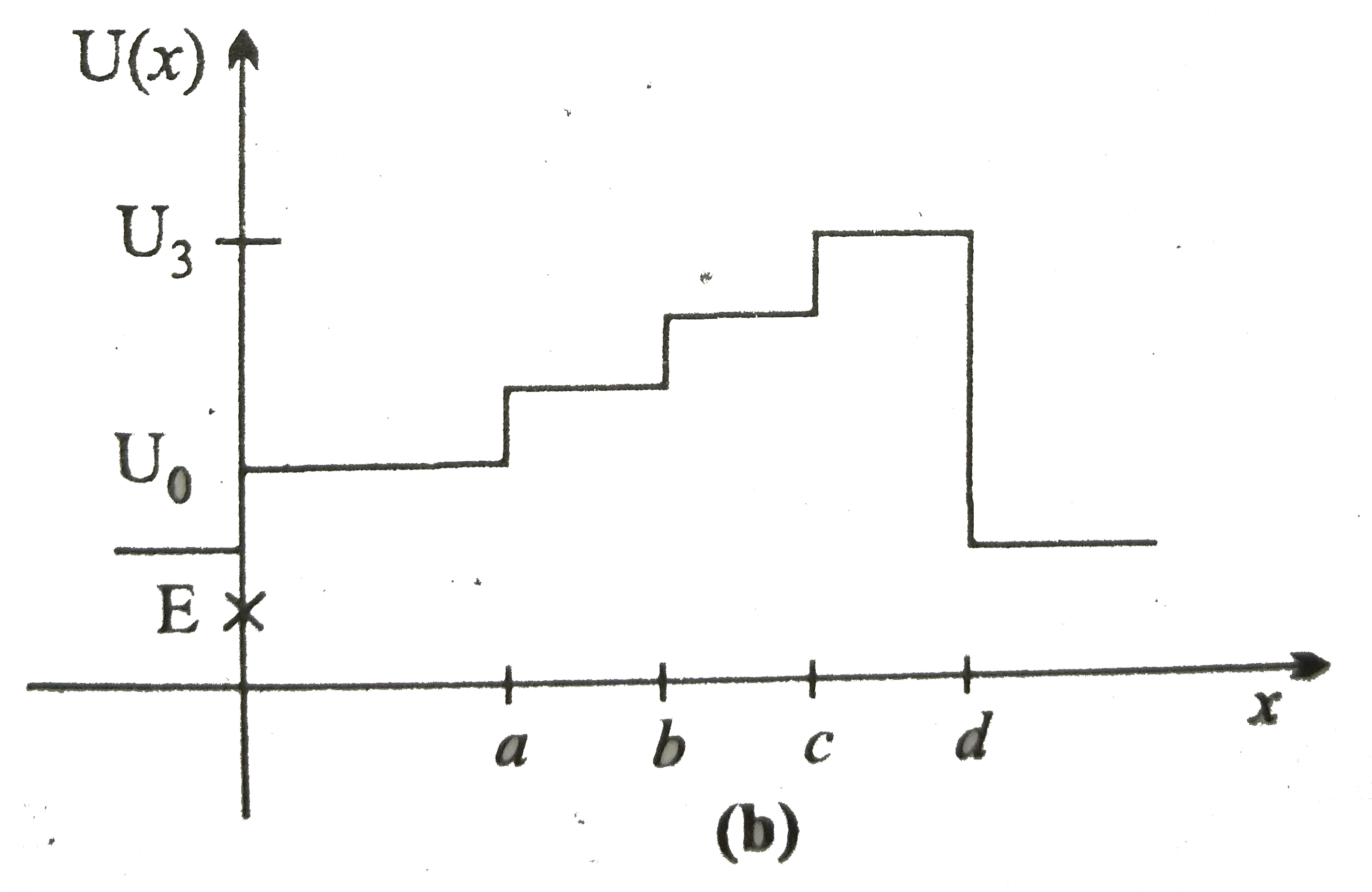 View Solution
View Solutionचित्र में कुछ एकविमीय स्थितिज ऊर्जा - फलनों के उदाहरण दिए गए हैं । कण की कुल ऊर्जा कोटि - अक्ष पर क्रॉस द्वारा निर्देशित की गई है । प्रत्येक स्थिति में, कोई ऐसे क्षेत्र बताइए, यदि कोई हैं तो, जिनमें दी गई ऊर्जा के लिए, कण को नहीं पाया जा सकता । इसके अतिरिक्त, कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिए । कुछ ऐसे भौतिक संदर्भो के विषय में सोचिए जिनके लिए ये स्थितिज ऊर्जा आकृतियाँ प्रासंगिक हों ।
(c)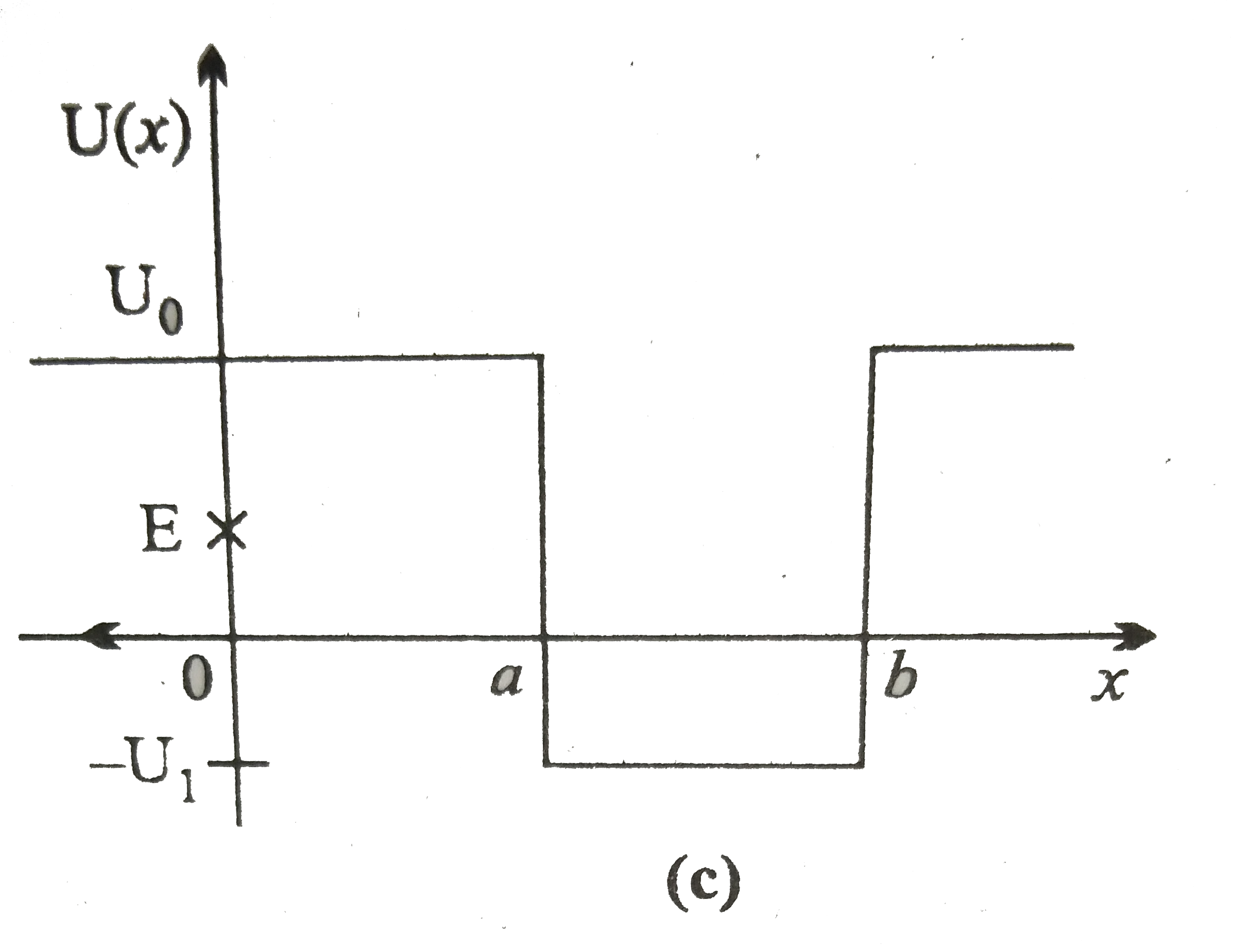 View Solution
View Solutionचित्र में कुछ एकविमीय स्थितिज ऊर्जा - फलनों के उदाहरण दिए गए हैं । कण की कुल ऊर्जा कोटि - अक्ष पर क्रॉस द्वारा निर्देशित की गई है । प्रत्येक स्थिति में, कोई ऐसे क्षेत्र बताइए, यदि कोई हैं तो, जिनमें दी गई ऊर्जा के लिए, कण को नहीं पाया जा सकता । इसके अतिरिक्त, कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिए । कुछ ऐसे भौतिक संदर्भो के विषय में सोचिए जिनके लिए ये स्थितिज ऊर्जा आकृतियाँ प्रासंगिक हों ।
(d)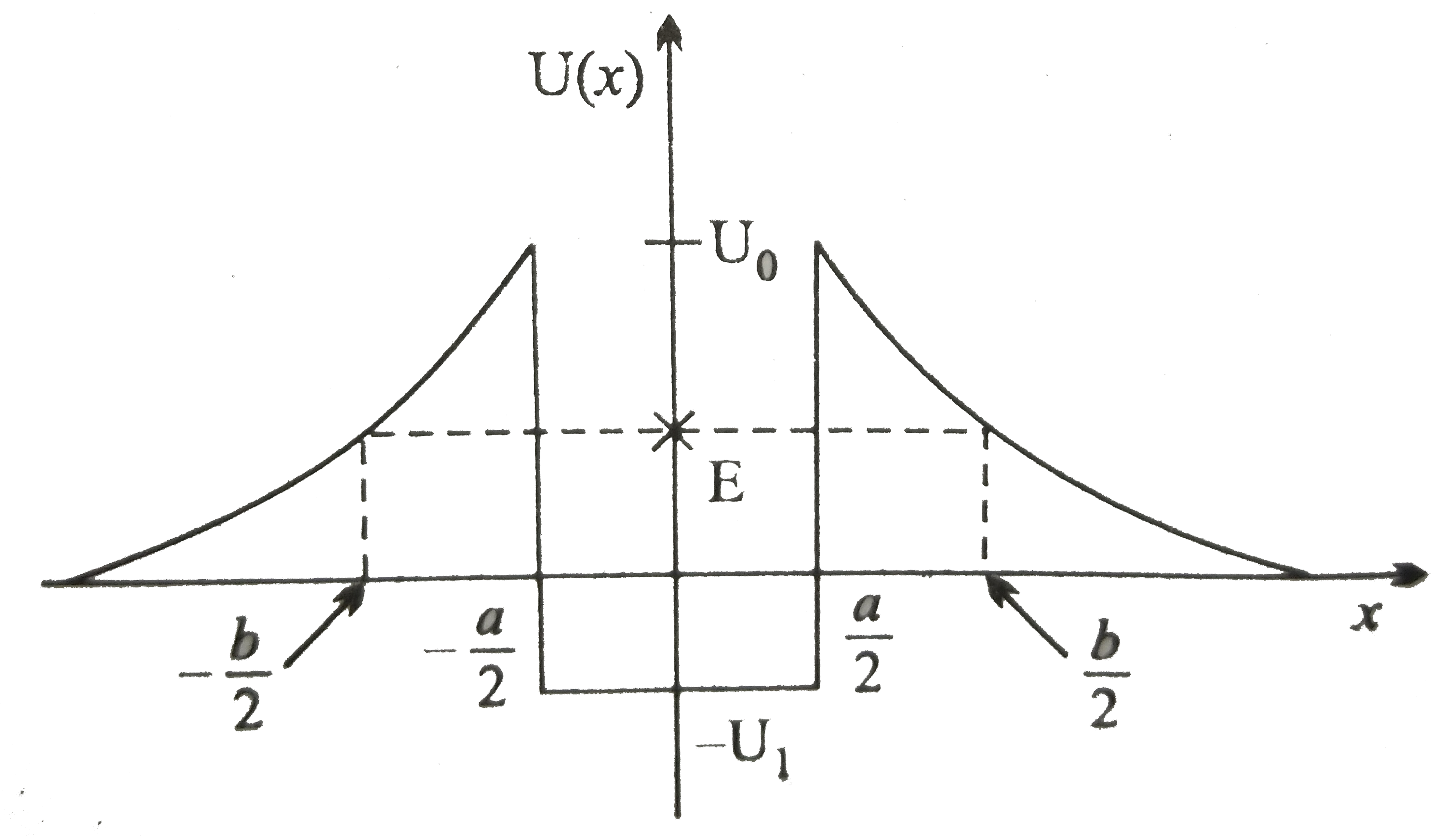 View Solution
View SolutionA particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when
View SolutionConsider a one - dimensional motion a a particle with total energy E . There are four regions A,B,C and D in which the relation between potential energy V , kinetic energy (K) and total energy E is as given ahead :
State with reason in each case whether a particle can be found in the given region or not .View Solution

