The potential energy U of a body of unit mass moving in one dimensional conservative force field is given by U=x2−4x+3. All units are is SI. For this situation mark out the correct statement (s).
The body will perform simple harmonic motion about x=2 units.
The body will perform oscillatory motion but not simple harmonic motion.
The body will perform simple harmonic motion with time period √2πs.
If speed of the body at equilibrium position is 4ms, then the amplitude of oscillation would be 2√2m
The correct Answer is:A, C, D
U=x2−4x+3 and F=−dUdx=−(2x−4)
At equilibrium position F=0, so x=2cm
Let the particle is displaced by △x from equilibrium position i.e, from x=2, then restoring force on body is
F=−2(2+△x)+4=−2△x
i.e., Fα−△x, so performs simple harmonic motion about x=2m
Time period T=2π√mk=2π√12=√2πs
From energy conservation, mv2max2+Umin=Umax
1×422+(22−4×2+3)=(A+2)2−4(A+2)+3
Where A is amplitude solving the above equation we get A=2√2m.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Comprehension
33 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
The potential energy (U) of a body of unit mass moving in a one-dimension force field is given by
U=(x2−4x+3) . All units are in S.L
View SolutionThe potential energy (U) of a body of unit mass moving in a one-dimension foroce field is given by
U=(x2−4x+3) . All untis are in S.L
View SolutionThe potential energy of an object of mass m moving in xy plane in a conservative field is given by U = ax + by , where x and y are position coordinates of the object. Find magnitude of its acceleration :-
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionS1: If the internal forces within a system are conservative, then the work done by the external forces on the system is equal to the change in mechanical energy of the system.
S2: The potential energy of a particle moving along x− axis in a conservative force field is U=2x2−5x+1 is S.I. units. No other forces are acting on it. It has a stable equalibrium position at one point on x− axis.
S3:Internal forces can perform net work on a rigid body.
S4: Internal forces can perform net work on a non− rigid body.
View SolutionPotential energy v/s position curve for one dimensional conservative field is shown. Force at A and B is respectively.

View SolutionThe potential energy of body of mass 2 kg moving along the x-axis is given by U=4x2, where x is in metre. Then the time period of body (in second) is
View SolutionThe potential energy of a conservative force field is given by
U=ax2−bx
where, a and b are positive constants. Find the equilibrium position and discuss whether the equilibrium is stable, unstable or neutral.
View SolutionGiven below is the plot of a potential energy function U(x) for a system, in which a particle is in one dimensional motion, while a conservative force F(x) acts on it. Suppose tha Emech= 8 J, the incorrect statement for this system is :
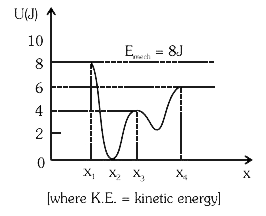
A. at x > x4, K.E. is constant throughout the region.
B. at x < x1 K.E. is smallest and the particle is moving at the slowest speed.
C. at x = x2 , K.E is greatest and the particle is moving at the fastest speed.
D. at x = x3, K.E. = 4 J
View SolutionA hydrogen atom having kinetic energy E collides with a stationary hydrogen atom. Assume all motions are taking place along the line of motion of the moving hydrogen atom. For this situation, mark out the correct statement (s).
View Solution
