The radii of the two columne is U-tube are and . When a liquid of density (angle of contact is is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is
acceleration due to gravity)
The correct Answer is:A
To solve the problem, we need to find the surface tension (T) of the liquid in the U-tube based on the given parameters. Here’s the step-by-step solution:
Step 1: Understand the setup
We have a U-tube with two columns of liquid. The radii of the two arms are r1 and r2 (where r2>r1). When a liquid of density ρ is filled in the U-tube, there is a height difference h between the two arms.
Step 2: Write the pressure balance equation
At equilibrium, the pressure at the same horizontal level in both arms must be equal. We can express this as:
P1=P2
Where:
- P1 is the pressure at the lower level in the left arm (with radius r1).
- P2 is the pressure at the lower level in the right arm (with radius r2).
Step 3: Express the pressures
The pressure at point 1 can be expressed as:
P1=P0−2Tr1+ρgh
And the pressure at point 2 can be expressed as:
P2=P0−2Tr2
Where P0 is the atmospheric pressure, T is the surface tension, and g is the acceleration due to gravity.
Step 4: Set the pressures equal
Setting P1 equal to P2:
P0−2Tr1+ρgh=P0−2Tr2
Step 5: Simplify the equation
Cancel P0 from both sides:
−2Tr1+ρgh=−2Tr2
Rearranging gives:
ρgh=2Tr2−2Tr1
Step 6: Factor out the surface tension
Factoring out 2T:
ρgh=2T(1r2−1r1)
Step 7: Solve for surface tension
Rearranging for T:
T=ρgh2(1r2−1r1)
Finding a common denominator:
T=ρgh⋅r1r22(r2−r1)
Final Answer
Thus, the surface tension T is given by:
T=ρgh⋅r1r22(r2−r1)
We have a U-tube with two columns of liquid. The radii of the two arms are r1 and r2 (where r2>r1). When a liquid of density ρ is filled in the U-tube, there is a height difference h between the two arms.
At equilibrium, the pressure at the same horizontal level in both arms must be equal. We can express this as:
P1=P2
Where:
- P1 is the pressure at the lower level in the left arm (with radius r1).
- P2 is the pressure at the lower level in the right arm (with radius r2).
The pressure at point 1 can be expressed as:
P1=P0−2Tr1+ρgh
And the pressure at point 2 can be expressed as:
P2=P0−2Tr2
Where P0 is the atmospheric pressure, T is the surface tension, and g is the acceleration due to gravity.
Setting P1 equal to P2:
P0−2Tr1+ρgh=P0−2Tr2
Cancel P0 from both sides:
−2Tr1+ρgh=−2Tr2
Rearranging gives:
ρgh=2Tr2−2Tr1
Factoring out 2T:
ρgh=2T(1r2−1r1)
Rearranging for T:
T=ρgh2(1r2−1r1)
Finding a common denominator:
T=ρgh⋅r1r22(r2−r1)
Thus, the surface tension T is given by:
T=ρgh⋅r1r22(r2−r1)
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Level 2 More Than One Correct
Explore 10 Videos
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Level 2 Comprehension Based
Explore 7 Videos
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Subjective Question
Explore 2 Videos
- EXPERIMENTSBook:DC PANDEY ENGLISHChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
The radii of the two columns is U-tube are r1 and r2(r2>r1). When a liquid of density ρ (angle of contact is 0∘)) is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is
(g= acceleration due to gravity)
View SolutionIn a U-tube the radii of two columns are respectively r1andr2 and if a liquid of density d filled in it has level difference of h then the surface tension of the liquid is -

View Solution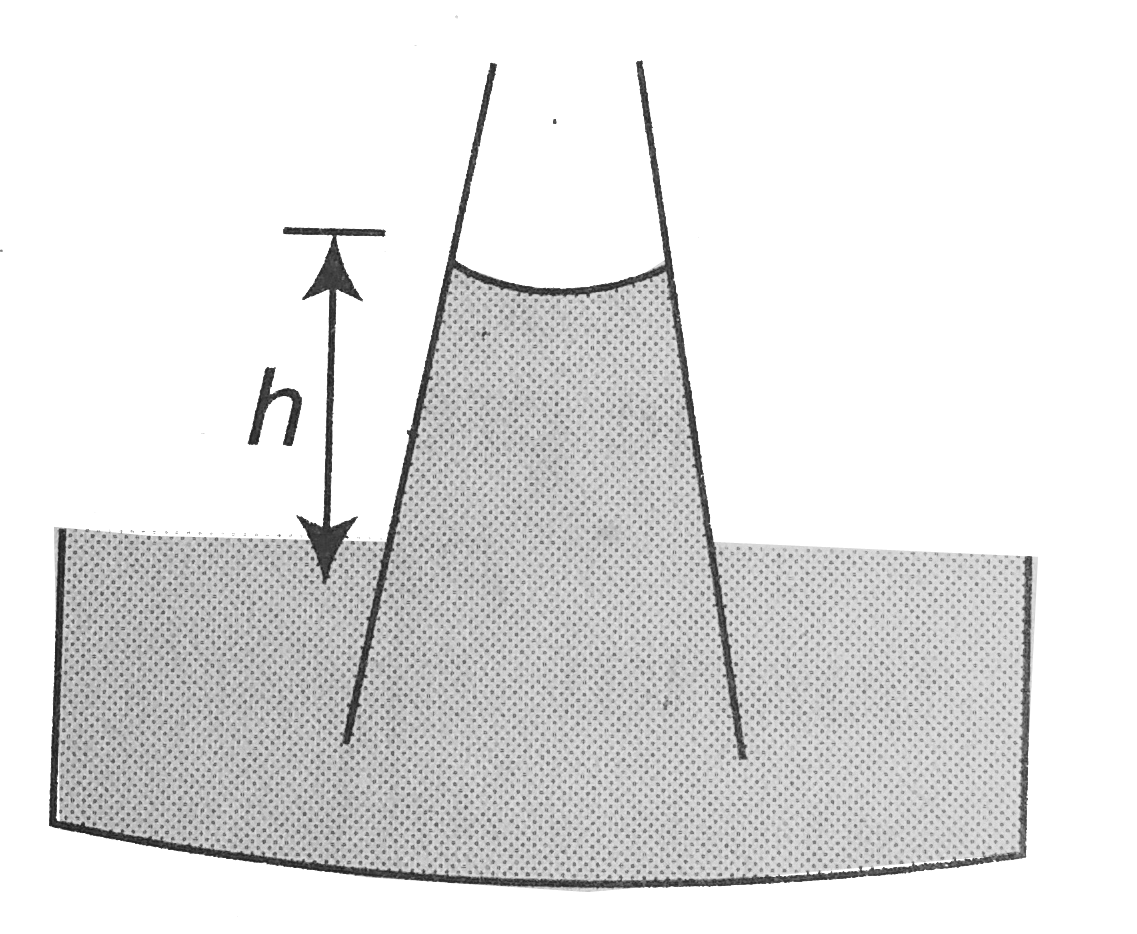
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:
View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
View SolutionA capillary tube of radius r is lowered into a liquid of surface tension T and density ρ. Given angle of contact =0∘.
What is the potential energy acquired by the liquid in the capillary?
View SolutionTwo holes are made at depths h and 2h from the top. A liquid of density ρ and height h is filled over another liquid of density 2ρ. Speeds of liquid ejecting from two holes are say v1 and v2.

If density of lower liquid is increased
View SolutionThe absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View SolutionWhat is the height to which a liquid rises between two long parallel plates, a distance d apart ? (Surface tension of liquid is T and density is ρ)
View SolutionWhen a vertical capillary of length with the sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is ρ, the inside diameter the capillary is d, the contact angle is θ, the atmospheric pressure is ρ0. Find the surface tension of the liquid. (Temperature this process remains constant.)

View SolutionWhen a vertical capillary of length l with a sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is ρ, the inside diameter the capillary is d, the contact angle is θ, the atmospheric pressure is ρ0. Find the surface tension of the liquid. (Temperature in this process remains constant.)

View Solution
