The rear side of a truck is open and a box of 40 kg mass is placed 5 m from the open end The coefficient of friction between the box and the surface below it is 0.15 On a straight road the truck starts from rest and accelerates with At what distance from the starting point does the box fall off the truck ? Ignore the size of the box .
To solve the problem, we will follow these steps:
Step 1: Identify the forces acting on the box
The box experiences two main forces:
1. The force due to the truck's acceleration.
2. The frictional force opposing the motion.
Given:
- Mass of the box, m=40kg
- Coefficient of friction, μ=0.15
- Acceleration of the truck, at=2m/s2
- Gravitational acceleration, g=9.8m/s2
Step 2: Calculate the maximum frictional force
The maximum frictional force Ffriction can be calculated using the formula:
Ffriction=μ⋅m⋅g
Substituting the values:
Ffriction=0.15⋅40⋅9.8=58.8N
Step 3: Calculate the force exerted on the box by the truck
The force Ftruck exerted on the box due to the truck's acceleration is given by:
Ftruck=m⋅at=40⋅2=80N
Step 4: Determine the net force acting on the box
The net force Fnet acting on the box can be calculated by subtracting the frictional force from the force exerted by the truck:
Fnet=Ftruck−Ffriction=80−58.8=21.2N
Step 5: Calculate the acceleration of the box
Using Newton's second law, the acceleration ab of the box can be calculated as:
ab=Fnetm=21.240=0.53m/s2
Step 6: Calculate the time until the box falls off the truck
The box is initially 5 m from the open end of the truck. We can use the equation of motion to find the time t it takes for the box to travel this distance:
s=ut+12abt2
Where:
- s=5m
- u=0 (initial velocity of the box relative to the truck)
- ab=0.53m/s2
Substituting the values:
5=0+12⋅0.53⋅t2
5=0.265t2
t2=50.265≈18.87
t≈4.34s
Step 7: Calculate the distance traveled by the truck in this time
Now we calculate the distance dt traveled by the truck in this time using the formula:
dt=ut+12att2
Where:
- u=0 (initial velocity of the truck)
- at=2m/s2
Substituting the values:
dt=0+12⋅2⋅(4.34)2
dt=1⋅18.84≈18.84m
Conclusion
The box will fall off the truck after the truck has traveled approximately 18.84 meters from the starting point.
---
The box experiences two main forces:
1. The force due to the truck's acceleration.
2. The frictional force opposing the motion.
- Mass of the box, m=40kg
- Coefficient of friction, μ=0.15
- Acceleration of the truck, at=2m/s2
- Gravitational acceleration, g=9.8m/s2
The maximum frictional force Ffriction can be calculated using the formula:
Ffriction=μ⋅m⋅g
Substituting the values:
Ffriction=0.15⋅40⋅9.8=58.8N
The force Ftruck exerted on the box due to the truck's acceleration is given by:
Ftruck=m⋅at=40⋅2=80N
The net force Fnet acting on the box can be calculated by subtracting the frictional force from the force exerted by the truck:
Fnet=Ftruck−Ffriction=80−58.8=21.2N
Using Newton's second law, the acceleration ab of the box can be calculated as:
ab=Fnetm=21.240=0.53m/s2
The box is initially 5 m from the open end of the truck. We can use the equation of motion to find the time t it takes for the box to travel this distance:
s=ut+12abt2
Where:
- s=5m
- u=0 (initial velocity of the box relative to the truck)
- ab=0.53m/s2
5=0+12⋅0.53⋅t2
5=0.265t2
t2=50.265≈18.87
t≈4.34s
Now we calculate the distance dt traveled by the truck in this time using the formula:
dt=ut+12att2
Where:
- u=0 (initial velocity of the truck)
- at=2m/s2
dt=0+12⋅2⋅(4.34)2
dt=1⋅18.84≈18.84m
The box will fall off the truck after the truck has traveled approximately 18.84 meters from the starting point.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISES
40 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Additional Examples / Exercises
6 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Short Answer Questions
26 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
Similar Questions
The rear side of a truck is open and a box of 40 kg mass is placed 5 m from the openend as shown The coefficient of friction between the box and the surface below it is 0.15 On a straight road the truck starts from rest and accelerates with 2ms−2 At what distance from the starting point does the box fall off the truck ? (Ignore the size of the box )
 .
.
View SolutionThe rear side of a truck is open and a box of 40 kg mass is placed 5 m from the open end The coefficient of friction between the box and the surface below it is 0.15 On a straight road the truck starts from rest and accelerates with 2m/s2 At what distance from the starting point does the box fall off the truck ? Ignore the size of the box .
View Solution
Knowledge Check
The rear side of a truck is open and a box of 40 kg mass is placed 5 m away from the open end as shown in figure. The coefficient of friction between the box the surface below it is 0.15. On a straight road, the truck starts from rest and accelerates with 2ms−2). At what distance from the starting point does the box fall from the truck ? (Ignore the size of the box.)
 A20 mB10mC√20mD5m
A20 mB10mC√20mD5mThe rear side of a truck is open A box of 40kg mass is placed 5m away from the open end as shown in The coefficient of friction between the box and the surface is 0.15. On a straight road, the truck starts from rest and accel erating with 2m/s2. At what dis tance from the starting point does the box dis-tance from the starting point does the box fall from the truck? (Ignore the size of the box)
 .A20mB10mC√20mD5m
.A20mB10mC√20mD5mThe rear side of a truck is open and a box of mass 20kg is placed on the truck 4 meters away from the open end coofficent of friction between truck and block is 0.15 the truck starts from rest with an acceleration of 2m/sec2on a straight road The box will fall off the truck when truck is at a distance from the starting point equal to(g=10m/s2)
A4metresB8 metresC16 metresD32metres
The rear side of a truck is open. A box of 40kg mass is placed 5m away from the open end as shown in figure. The coefficient of friction between the box and the surface is 0.15. On a straight road, the truck starts from rest and accel erating with 2m/s2. At what distance from the starting point does the box fall off the truck? Ignore the size of the box
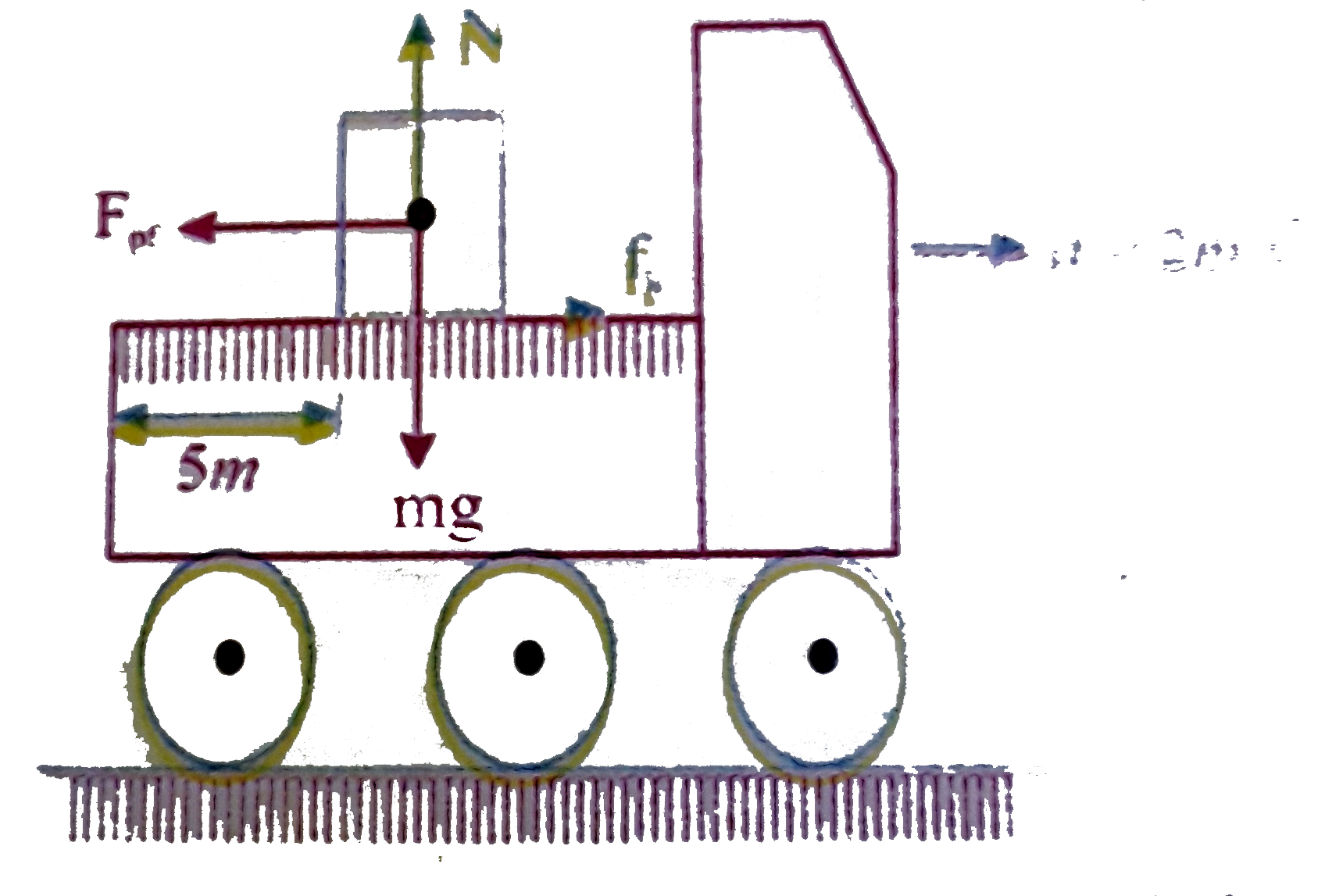
View SolutionThe rear side of a truck is open and a box of mass 20kg is placed on the truck 4m away from the open end μ=0.15 and g=10m/s2 The truck starts from rest with an acceleration of 2m/s2 on a straight road The box will fall off the truck when it is at a distance from the starting point equal to .
View SolutionThe rear side of a truck is open and a box of mass 2kg is placed on the truck 8meters away from the open end. μ=0.1 and g=10m/s2. The truck starts from rest with an acceleration of 2m/s2 on a straight road. The box will fall off the truck when it is at distance from the starting point equal to
View SolutionA box mass m kg is placed on the rear side of an open truck acceleration at 4ms−2 . The coefficient of friction between the box ant the surface below it is 0.4 . The net acceleration of the box with respect to the truck is zero. The value of m is.
View SolutionA block of mass 15kg is placed on a long trolley. The cofficient of fricition between the block and trolley is 0.18. The trolley accelerates from rest with 0.5m/s2 for 20s. then what is the friction force:-
View Solution
