The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
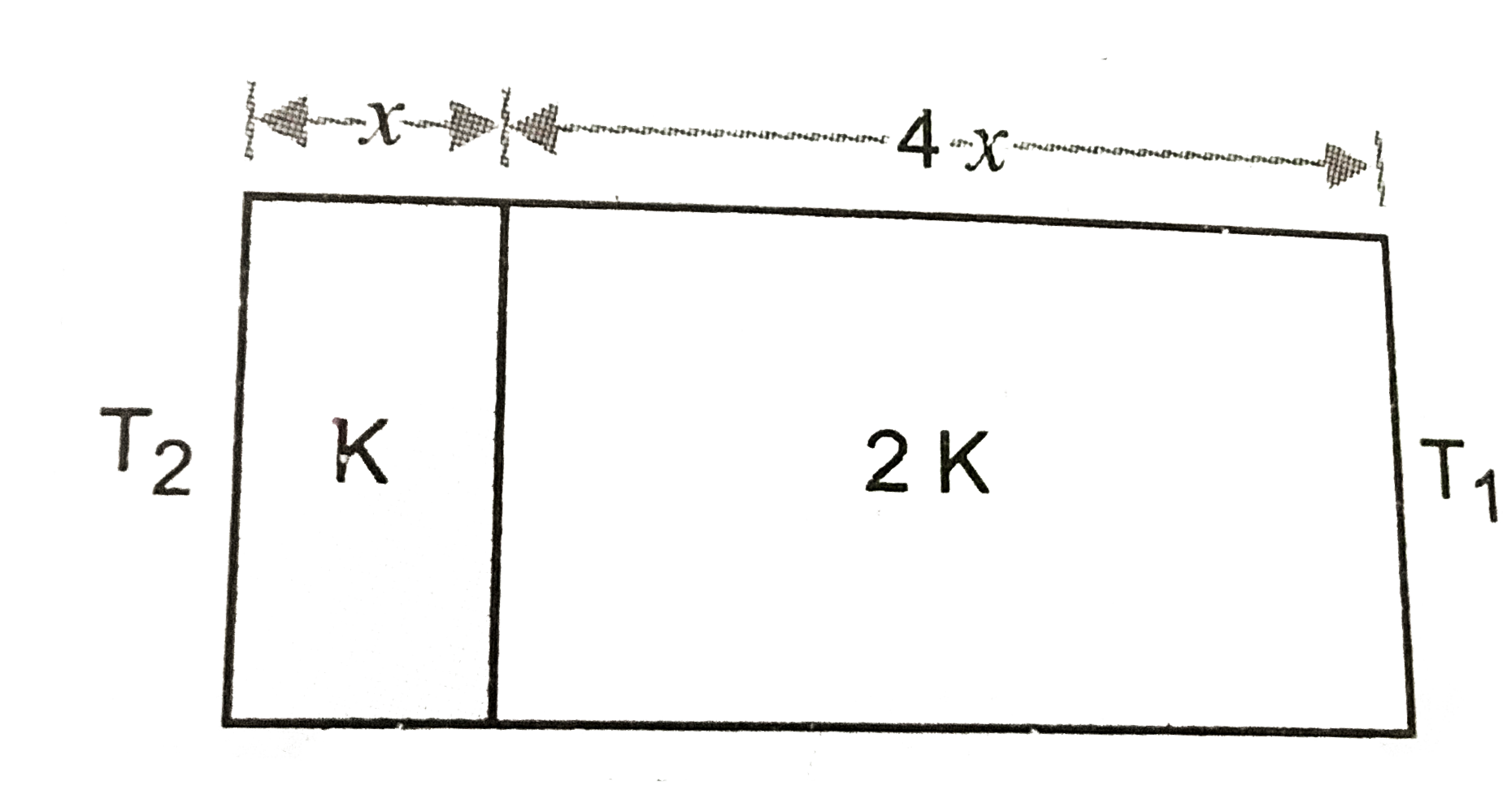
1
12
23
13
The correct Answer is:D
Let the temperature of common interface be T K
Rate of heat flow H=Qt=KAΔTl
∴H=(Qt)1=2KA(T−T1)4x
and H2=(Qt)2=KA(T2−T)x
In steady state the rate of heat flow should be same in whole system i.e.,
H1=H2
or 2Ka(T−T1)4x=KA(T2−T)x
T−T12=T2−T or T−T1=2T2−2T
T=2T2+T13.....(i)
Hence, heat flow composite slab is
H=[Ka(T2−T)x]=KAx(T2−2T2−T13) [From eqn. (i)]
=KA3x(T2−T1)
According to question, H=[A(T2−T1)Kx]f.....(iii)
By comparing eqs. (ii) and (iii), we get f=13
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTIPSChapter:THERMAL PROPERTIES OF MATTERExercise:NCERT Exemplar
Explore 8 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTIPSChapter:THERMAL PROPERTIES OF MATTERExercise:Assertion And Reason
Explore 10 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTIPSChapter:THERMAL PROPERTIES OF MATTERExercise:Newton'S Law Of Cooling
Explore 3 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTIPSChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:Assertion And Reason
Explore 15 Videos
- THERMODYNAMICSBook:NCERT FINGERTIPSChapter:THERMODYNAMICSExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T2 and T1(T2>T1). The rate of heat of heat transfer through the slab, in ? steady state is [(AT2−T1x]f, with f equal to :-

View SolutionTwo materials having coefficients of thermal conductivity ‘3 K’ and ‘K’ and thickness ‘d’ and ‘3 d’, respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are θ2 and θ1 respectively, (θ2>θ1) The temperature at the interface is:
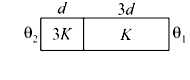
View Solution
Knowledge Check
The temperature of the two outer surfaces of a composite slab consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab in steady state is (AK(T2−T1)x)f. where, f is equal to
 .A1B1/2C2/3D1/3
.A1B1/2C2/3D1/3The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x, respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)Kx)f, with f equals to
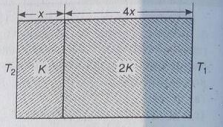 A1B1/2C2/3D1/3
A1B1/2C2/3D1/3The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x, respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)Kx)f, with f equals to
 A1B1/2C2/3D1/3
A1B1/2C2/3D1/3
A composite slab consists of two rectangular slabs of different materials, having coefficients of conductivity 2K and K. The two ends of the slabs are at temperatures T1 and T2 (where T1>T2 ). How will the rate of heat flow depend on a where 3a and a are the lengths of two slabs? Consider that the two slabs have equal thickness.

View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materails having coefficients of two materails having coefficients of termal conductivity K and 2K and thickness x and 4x, respectively, are T2andT1(T1>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)K2)f, with f equal to
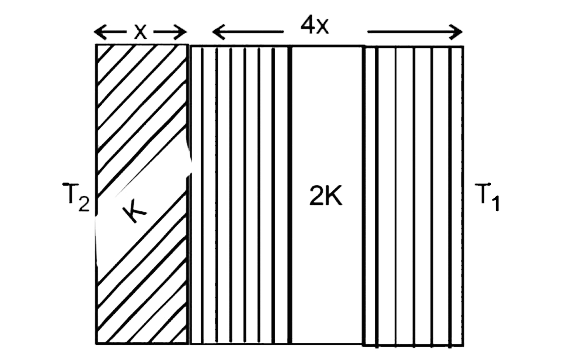
View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View Solution
The temperature across two different slabs A and B are shown I the steady state (as shown Fig) The ratio of thermal conductivities of A and B is
View Solution
