The three block shown in fig. move with constant velocities. Find the velocity of blocks A and B. given VP2=10ms−1⏐↓,VC=2ms−1↑⏐.

vA=vp2=10ms−1
Using shortcut method
For pulley P2
vP2=VB+(_VC)2
10=VB−22⇒vB=22ms−1.

Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.4
13 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.2
35 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
Knowledge Check
In the block moves up with constant velocity v m//s. Find F
 AF=mg2BF=2mg3CF=mg3DF=m3
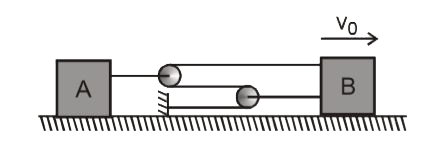
AF=mg2BF=2mg3CF=mg3DF=m3Block B moves to the right with a constant velocity v0. The velocity of body A relative to B is
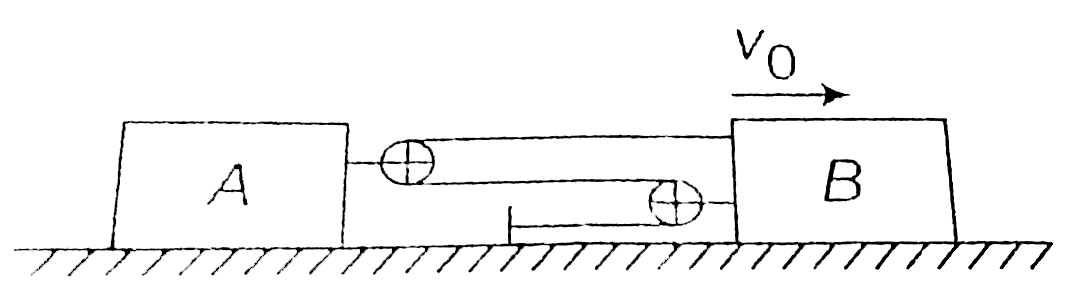 Av02, towards leftBv02, towards rightC3v02, towards leftD3v02, towards right
Av02, towards leftBv02, towards rightC3v02, towards leftD3v02, towards rightIn the arrangement shown, end A of light intextensible string is pulled with constant velocity v. the velocity of block B is
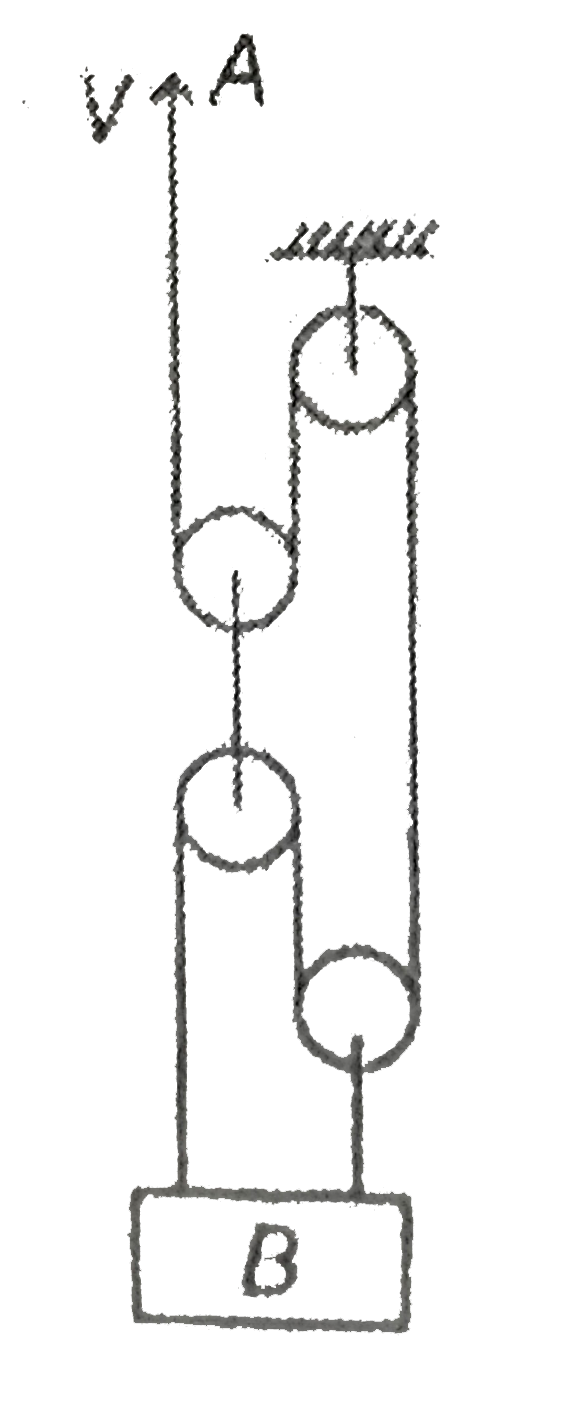 AV/2BvCv/3D3v
AV/2BvCv/3D3v
Figure shows a pulley over which is string passes and connected to two masses A and B. Pulley moves up with a velocity VP and mass B is also going up at a velocity VB.
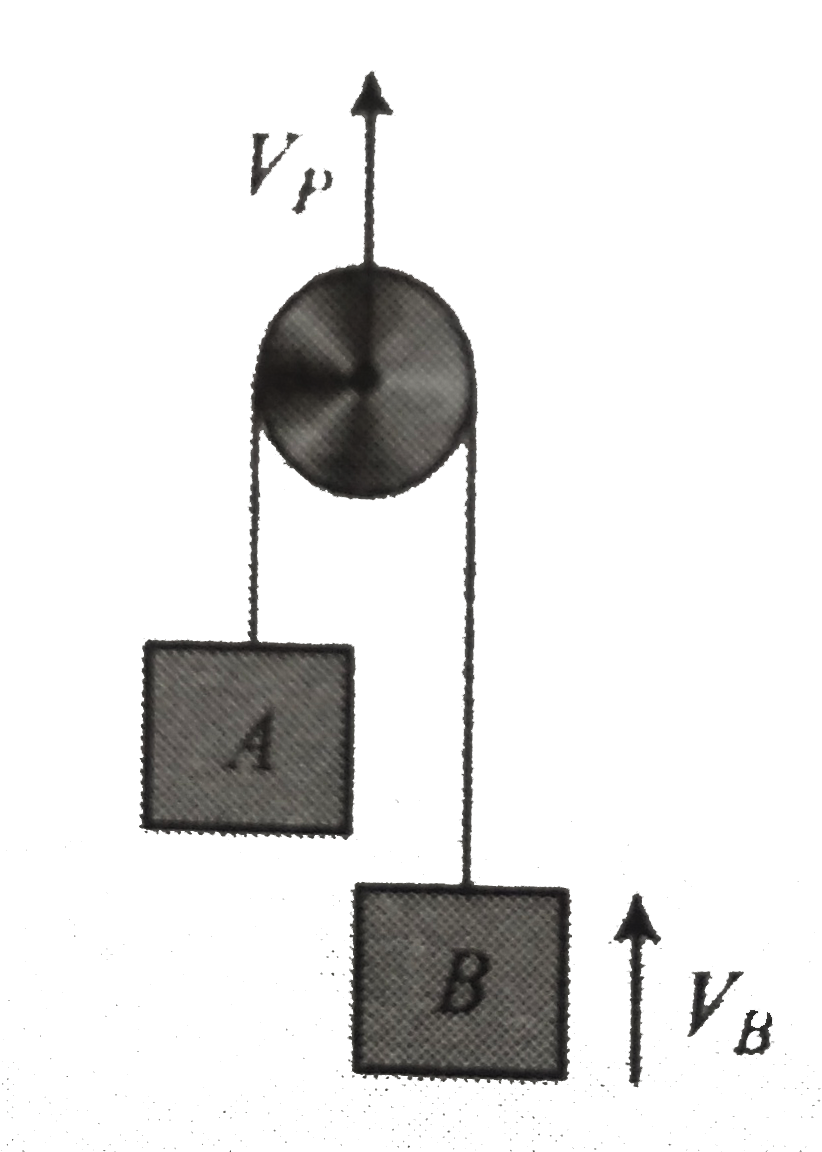
Find the velocity of mass A if
(a) VP=5ms−1 and VB=10ms−1
(b) VP=5ms−1 and VB=−20ms−1.
View SolutionThe block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal
View SolutionBlock 5 shown in figure moves to the right with a constant velocity of 30 cm/s. Find :

(a) The velocity of block A.
(b) The velocity of the point P of the string.
(c) The velocity of the point M of the string.
(d) The relative velocity of the point P of the string with respect to the block A.
View SolutionTwo blocks A and B are shown in figure. Block A moves to the left with a constant velocity of 6m/s. Find :
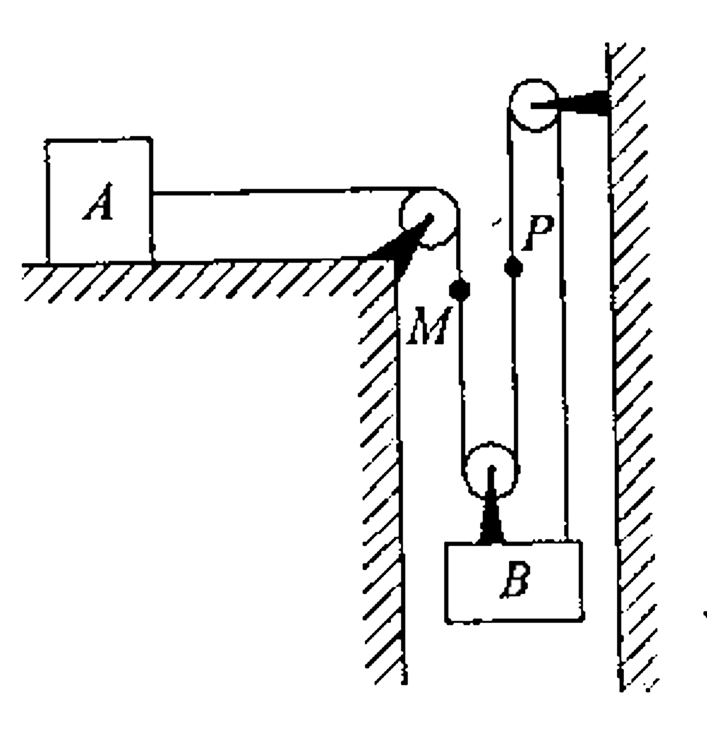
(a) Velocity of the blocks B.
(b) Velocity of the point P of the string.
Relative velocity of the point M of the cable with respect to the point P.
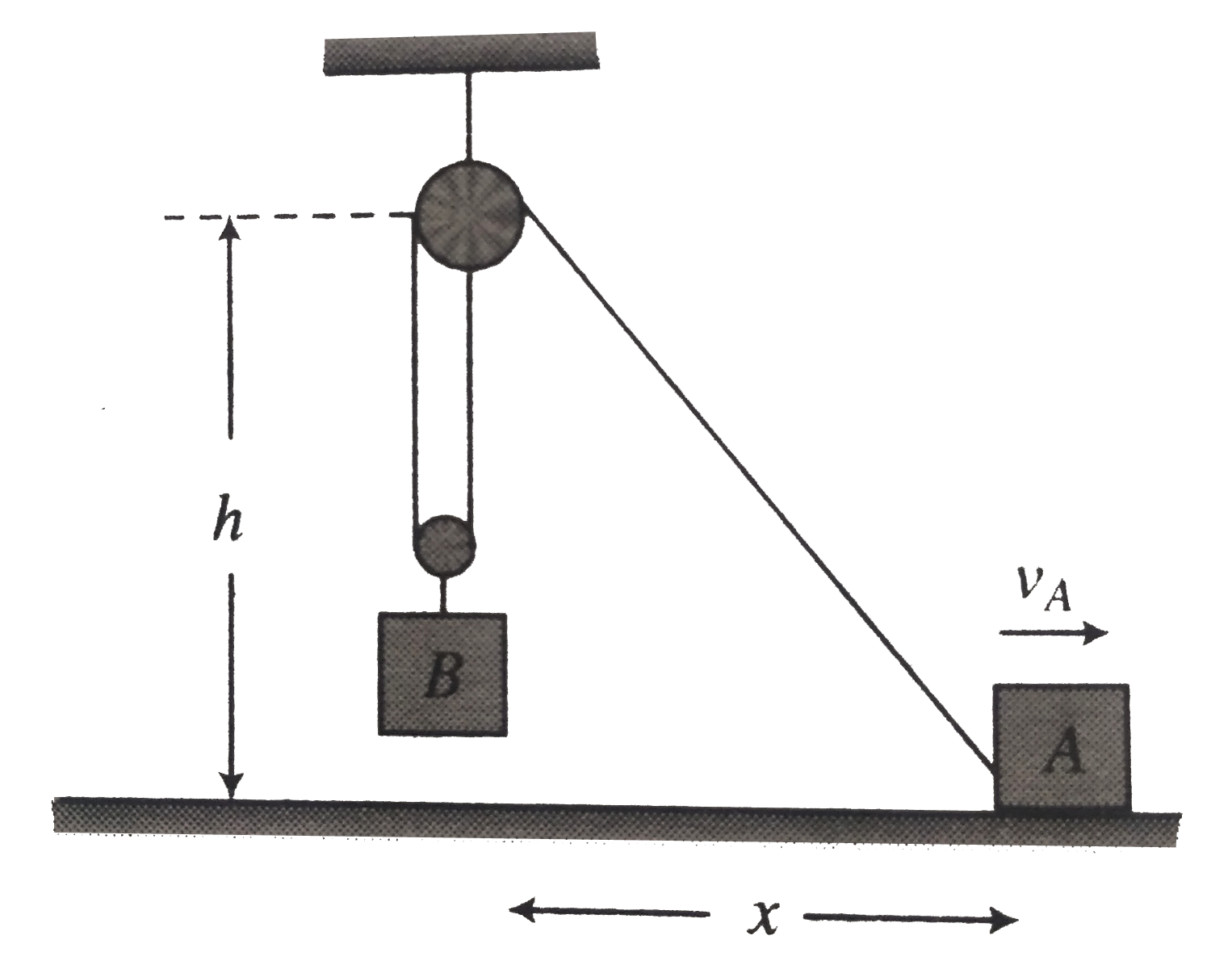
View SolutionIf block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
View Solution