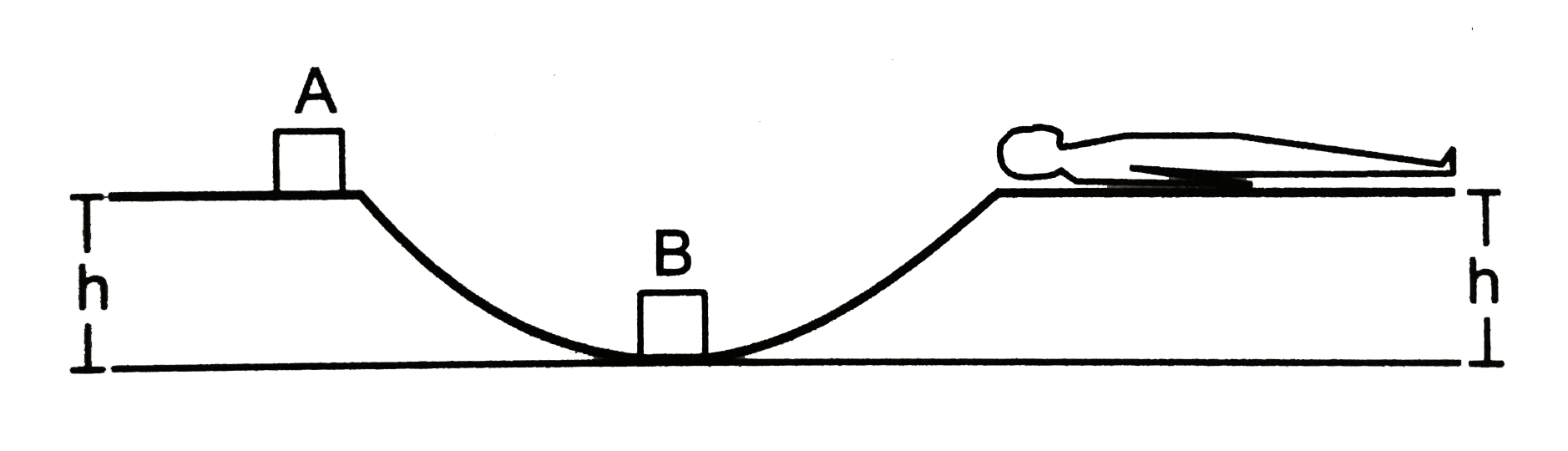
The track shown in figure is frictionless. The block B of mass 2 m is lying at rest and the block A of mass m is placed along the track with some speed. The collision between A and B is perfectly elastic. With what velocity should the block A be started to get the sleeping man awakened ?
 Solution in Tamil
Solution in Tamil
The correct Answer is:A, B
Let the velocity of
Let the fiN/Al velocity when reachign at B become collision
……..i
When the block B reached at the upper man's hed, the velocity of B is just zero.
rarr
ltbr>
After collision velocity fo v_A=V(say)v_B=sqrt(2gh):.mxxv_1+2mxx0=mxxv+2m+sqrt(2gh)rarr v_1-v=2sqrt(2gh)(1/2)xxmxxv_1^2+(1/2)xx2m(sqrt(2gh)^2)rarr v_1^2-v^2=2xxsqrt(2gh)xx2msqrt(2gh)((v_1+v)(v_1-v))/(v_1+v)=(2xxsqrt(2gh)xsqrt(2gh))/(2xxsqrt(2gh))rarr v_1+v=sqrt(2gh)2v_1=3sqrt(2gh)rarr v_1=(3/2)sqrt(2gh)But v_1=sqrt(2gh+u^2)=(3/2)sqrt(2gh)
So the block will travel with a velocity greater than i.e., man must awake.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CALORIMETRYBOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises
18 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
Similar Questions
The centre of mass of a system of particles is at the origin. It follows that:
View SolutionAn aluminium vessel of mass 0.5kg contains 0.2kg of water at 20∘C A block of iron of mass 0.2kgat100∘C is gently put into the water .Find the equilibrium temperature of the mixture, Specific heat capacities of aluminium , iron and water are 910Jkg−1K−1470Jkg−1K−1and4200Jkg−1K−1 respectively
View SolutionFind the accelerationof the moon with respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution around the earth =27.3days
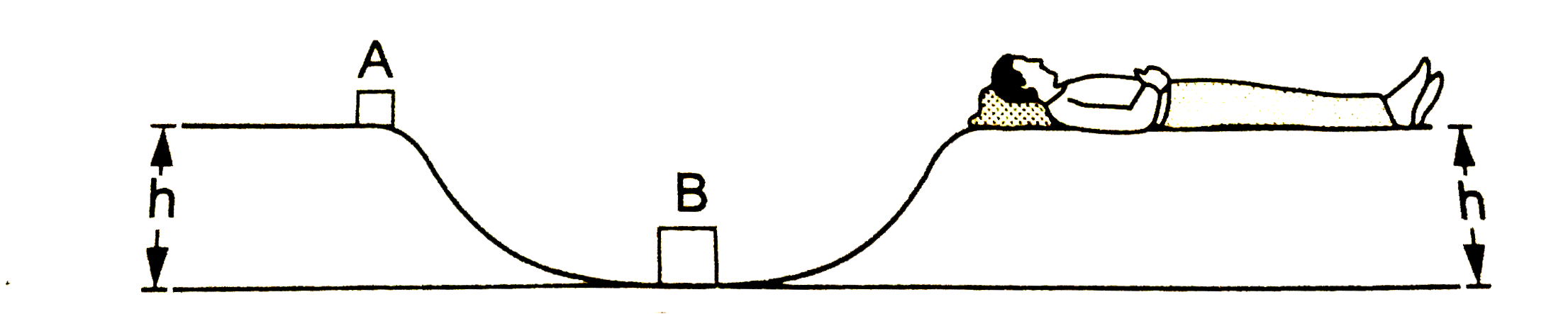
View SolutionThe track shown in figure is frictionles. The block B of mass 2m is lying at rest and the block A of mass m is pushed along the track with some speed. The collision etwen A and B is perfectly elastic. With what velocity should the block A be started to get teh sleepign mn awakenend?
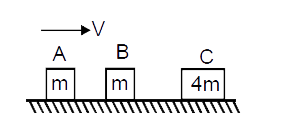
View SolutionThree blocks are initially placed as shown in the figure. Block A has mass m and initial velocity v to the right. Block B with mass m and block C with mass 4 m are both initially at rest. Neglect friction. All collisions are elastic. The final velocity of block A is
View SolutionA small block of mass m slides along a smooth frictionless track as shown. (a) If it starts from rest at P , what is the resultant force acting on it at Q ? (b) At what height above the bottom should the block be released so that the force it exerts against the track at the top of the loop equals its weight?
View SolutionThree blocks A, B and C each of mass m are placed on a surface as shown in the figure. Blocks B and C are initialyy at rest. Block A is moving to the right with speed v. It collides with block B and stricks to it. The A-B combination collides elastically with block C. Which of the following statement is (are) true about the velocity, of block B and C.

View SolutionA block of mass m is placed on a circular track and then it is given a velocity upsilon vertically downwards at position A on track. If block moves on track with constant speed, then
View SolutionThere are hundred indentical blocks equally spaced on a frictionless track as shown in the figure . Initially , all the blocks are separate . Each collision is perfectly inelastic . The final velocity will be
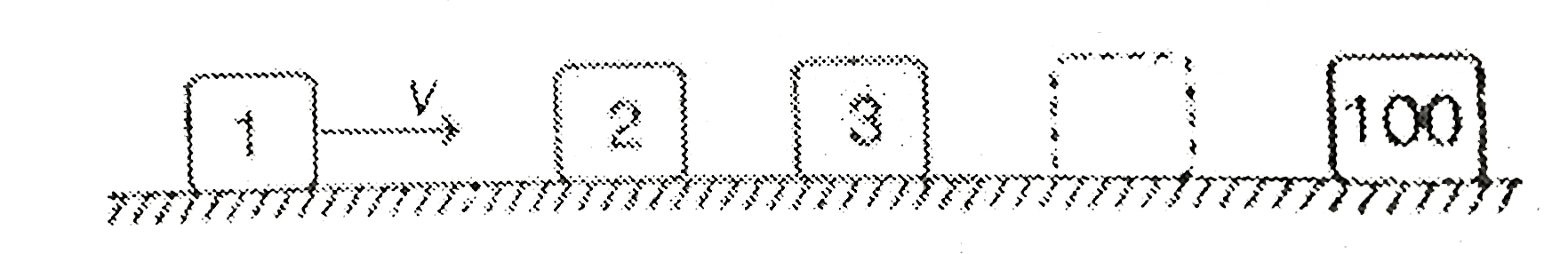
View Solutionचित्र में एक घर्षणरहित पथ दिखाया गया है। 2m द्रव्यमान का एक ब्लॉक B इस पथ पर स्थिर रखा हुआ है तथा m द्रव्यमान का एक ब्लॉक A इस पथ पर दाहिनी और गोतशल कर दिया गया है। A तथा B में होनेवाली टक्कर पूर्णतया प्रत्यास्थ है। ब्लॉक A को कम-से-कम किस चाल से चलना प्रारंभ करना चाहिए ताकि सोया हुआ व्यक्ति जाग जाए?
View SolutionThree blocks are initially placed as shown in the figure. Block A has mass m and initial velocity v to the right. Block B with mass m and block C with mass 4 m are both initially at rest. Neglect friction. All collisions are elastic. The final velocity of block A is

View SolutionA block of mass m is placed on a vertical fixed circular track and then it is given velocity v along the track at position A on track. The coefficient of friction between the block and the track varies with the angle θ . If the block moves on track with constant speed then the coefficient of friction is
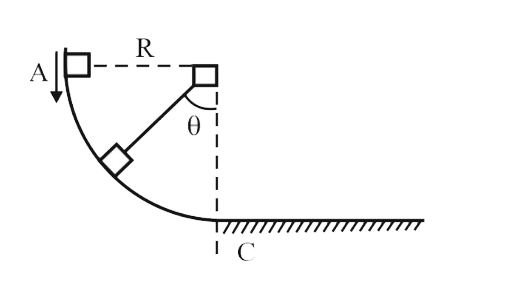
View SolutionA small block of mass m slides along a smooth frictional track as shown in the figure. If it starts from rest at P, what is the resultant force acting on it at Q?
View SolutionThe track shown in the figure is frictionless. The block B of mass 4kg is lying at rest and block A of mass 2kg is pushed along the track with some speed. The collision between A and B is perfectly elastic. With that velocity should the block A start such that block B just reaches at point P ?
View SolutionBlock 1 of mass m1 slides along a frictionless floor and into a one-dimensional elastic collision with stationary block 2 of mass m2=3m1. Prior to the collision, the center of mass of the two block system had a speed of 3.00 m/s. Afterward, what are the speeds of (a) the center of mass and (b) block 2 ?
View SolutionA block of mass m is placed on a circular track and then it is given a velocity υ vertically downwards at position A on track. If block moves on track with constant speed, then

View Solution
