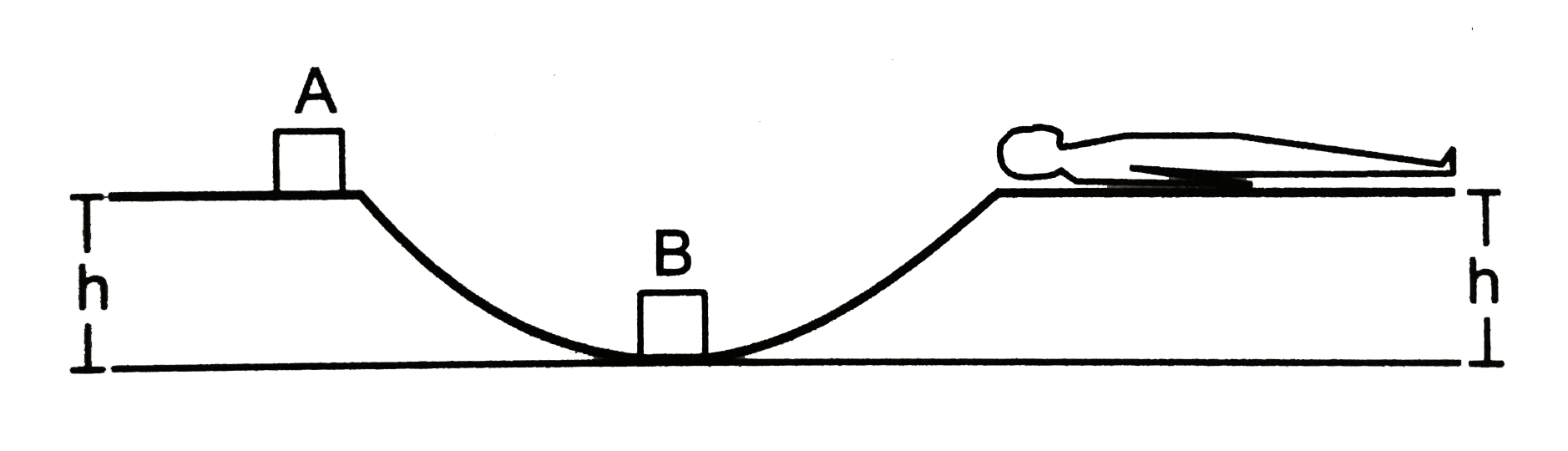
The track shown in figure is frictionles. The block B of mass 2m is lying at rest and the block A of mass m is pushed along the track with some speed. The collision etwen A and B is perfectly elastic. With what velocity should the block A be started to get teh sleepign mn awakenend?
The correct Answer is:A, B
Let the velocity of A=μ1
Let the fiN/Al velocity when reachign at B become collision =v1
∴(12)m21−(12)mv21=mgh
→v21−v21=2gh
→v1=√2gh+u21……..i
When the block B reached at the upper man's hed, the velocity of B is just zero.
∴(12)x2m×(0)2−(12)×2m×v2=mgh
rarr v=√2gh
∴BeforecollisonvelocityofuA=v1 ltbr> uB=0
After collision velocity fo v_A=V(say)<br>v_B=sqrt(2gh)<br>sinceitisanel∗iccollisionthemomentumandKbeconserved<br>:.mxxv_1+2mxx0=mxxv+2m+sqrt(2gh)<br>rarr v_1-v=2sqrt(2gh)<br>Also(1/2)xxmxxv_1^2+(1/2)xx2m(sqrt(2gh)^2)<br>rarr v_1^2-v^2=2xxsqrt(2gh)xx2msqrt(2gh)<br>Divgiandii<br>((v_1+v)(v_1-v))/(v_1+v)=(2xxsqrt(2gh)xsqrt(2gh))/(2xxsqrt(2gh))<br>rarr v_1+v=sqrt(2gh)<br>÷giandiii<br>2v_1=3sqrt(2gh)<br>rarr v_1=(3/2)sqrt(2gh)<br>But v_1=sqrt(2gh+u^2)<br>=(3/2)sqrt(2gh)<br>→2gh+u2=(94)(2gh)
u=√2.5gh
So the block will travel with a velocity greater than √2.5gh i.e., man must awake.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective 2
11 Videos
- CALORIMETRYBOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises
18 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
Similar Questions
Knowledge Check
The track shown in the figure is frictionless. The block B of mass 4kg is lying at rest and block A of mass 2kg is pushed along the track with some speed. The collision between A and B is perfectly elastic. With that velocity should the block A start such that block B just reaches at point P ?
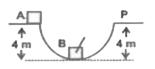 A10m/sB5m/sC20m/sD15m/s
A10m/sB5m/sC20m/sD15m/sA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it isAμgBμMmgCμmMgDgμA block of mass m slides down along the surface of the bowl from the rim to the bottom as shown in fig. The velocity of the block at the bottom will be-
 A√πRgB2√πRgC√2RgD√gR
A√πRgB2√πRgC√2RgD√gR
A block of mass m is at rest on a rought wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionThere are hundred indentical blocks equally spaced on a frictionless track as shown in the figure . Initially , all the blocks are separate . Each collision is perfectly inelastic . The final velocity will be
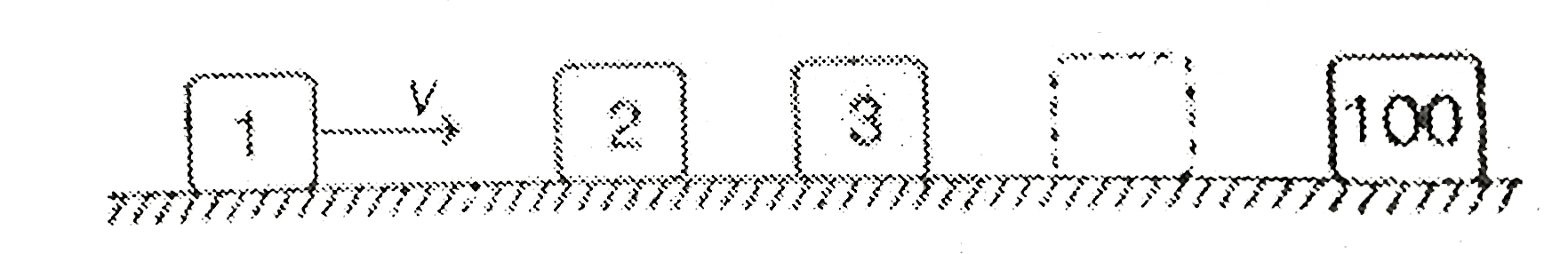
View SolutionA block of mass 2 kg is pushed towards a very heavy object moving with 2 m/s closer to the block (as shown). Assuming elastic collision and frictionless surface, find the final velocities of the blocks.

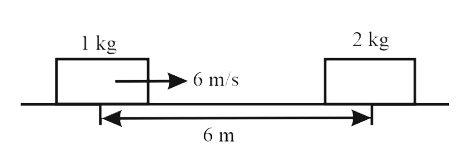
View SolutionA block of mass 1 kg is pushed towards another block of mass 2 kg from a 6 m distance as shown in the figure. If just after the collision, the velocity of 2 kg block is 4ms−1, then
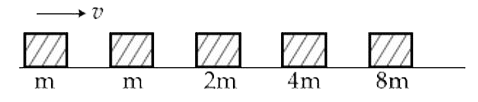
View SolutionBlocks of masses m , 2m , 4m and 8m are arranged in a line on a frictionless floor . Another block of mass m , moving with speed v along the same line (see figure ) collides with mass m in perfectly inelastic manner. All the subsequent collisions are also perfectly inelastic. By the time the last block of mass 8 m starts moving the total energy loss is p% of the original energy . Value of 'p' is close to :
View Solution