the uniform magnetic field perpendicualr to the plane of a conducting ring of radius a change at the rate of α, then
(a) all the points on the ring are at the same potential
(b) the emf induced in the ring is πa2α
( c) electric field intensity E at any point on the ring is zero
(d) E=(aα)/2
The correct Answer is:A, B, D
To solve the problem, we need to analyze the situation where a uniform magnetic field perpendicular to the plane of a conducting ring of radius a is changing at the rate of α. We will derive the induced electromotive force (emf) and the electric field in the ring step by step.
Step 1: Calculate the Magnetic Flux
The magnetic flux Φ through the conducting ring is given by the formula:
Φ=B⋅A
where B is the magnetic field and A is the area of the ring. The area A of the ring with radius a is:
A=πa2
Thus, the magnetic flux becomes:
Φ=B⋅πa2
Step 2: Relate the Change in Magnetic Field to Time
Given that the magnetic field B is changing at a rate α, we can express this as:
dBdt=α
Step 3: Apply Faraday's Law of Electromagnetic Induction
According to Faraday's law, the induced emf E in the ring is given by the negative rate of change of magnetic flux:
E=−dΦdt
Substituting the expression for magnetic flux, we have:
E=−ddt(B⋅πa2)
Since A is constant, we can write:
E=−πa2dBdt
Substituting dBdt=α:
E=−πa2α
The magnitude of the induced emf is:
|E|=πa2α
Step 4: Calculate the Induced Electric Field
The induced electric field E around the ring can be related to the induced emf by the formula:
E=∮E⋅dl
For a circular path of radius a, the length dl is the circumference:
dl=2πa
Thus, we have:
E=E⋅2πa
Substituting the expression for induced emf:
πa2α=E⋅2πa
Solving for E:
E=πa2α2πa=aα2
Step 5: Check the Potential Difference
To check if all points on the ring are at the same potential, we consider a small segment dl of the ring. The potential difference dV across this segment can be expressed as:
dV=E⋅dl
If we assume a current I flows through the ring, the potential drop across the resistance R of the ring can be expressed as:
dV=−I⋅dR
Since dR is proportional to dl, we find that the potential difference across any segment is zero if the induced electric field is uniform. Thus, all points on the ring are at the same potential.
Final Conclusion
The induced emf in the ring is πa2α, the induced electric field is aα2, and all points on the ring are at the same potential.
The magnetic flux Φ through the conducting ring is given by the formula:
Φ=B⋅A
where B is the magnetic field and A is the area of the ring. The area A of the ring with radius a is:
A=πa2
Thus, the magnetic flux becomes:
Φ=B⋅πa2
Given that the magnetic field B is changing at a rate α, we can express this as:
dBdt=α
According to Faraday's law, the induced emf E in the ring is given by the negative rate of change of magnetic flux:
E=−dΦdt
Substituting the expression for magnetic flux, we have:
E=−ddt(B⋅πa2)
Since A is constant, we can write:
E=−πa2dBdt
Substituting dBdt=α:
E=−πa2α
The magnitude of the induced emf is:
|E|=πa2α
The induced electric field E around the ring can be related to the induced emf by the formula:
E=∮E⋅dl
For a circular path of radius a, the length dl is the circumference:
dl=2πa
Thus, we have:
E=E⋅2πa
Substituting the expression for induced emf:
πa2α=E⋅2πa
Solving for E:
E=πa2α2πa=aα2
To check if all points on the ring are at the same potential, we consider a small segment dl of the ring. The potential difference dV across this segment can be expressed as:
dV=E⋅dl
If we assume a current I flows through the ring, the potential drop across the resistance R of the ring can be expressed as:
dV=−I⋅dR
Since dR is proportional to dl, we find that the potential difference across any segment is zero if the induced electric field is uniform. Thus, all points on the ring are at the same potential.
The induced emf in the ring is πa2α, the induced electric field is aα2, and all points on the ring are at the same potential.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Linked Comprehension
36 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Single Correct
79 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
the uniform magnetic field perpendicular to the plane of a conducting ring of radius a change at the rate of α, then
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is

View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionThe figure shows a non conducting ring of radius R carrying a charge q. In a circular region of Radius r, a uniform magnetic field B perpendicular to the plane of the ring varies at a constant rate dBdt=β. The torque on the ring is

View SolutionA ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field.If T=10sec, find the instant of time at which EMF will be maximum & minimum respectively :
View SolutionA ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field. Find the instant of time at which EMF will be maximum & minimum respectively. (Figure:
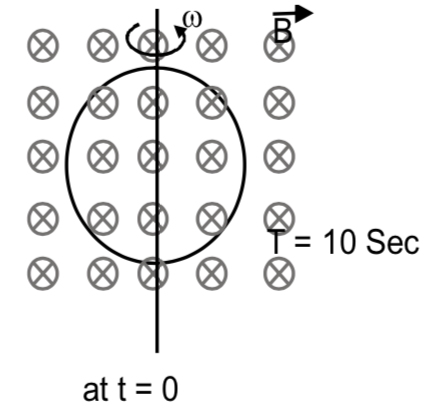 )
)
View SolutionA loop of irregular shape of conducting wire PORS (as shown in figure) placed in a uniform magnetic field perpendicular to the plane of the paper changes into a circular shape. The direction of induced current will be
View SolutionA vertical ring of radius r and resistance on R falls vertically. It is in contact with two vertical rails which are joined at the top. The rails are without friction and resistance. There is a horizontal uniform, magnetic field of magnitude B perpendicular to the plane of the ring and the rails. When the speed of the ring is v , the current in the section PQ is
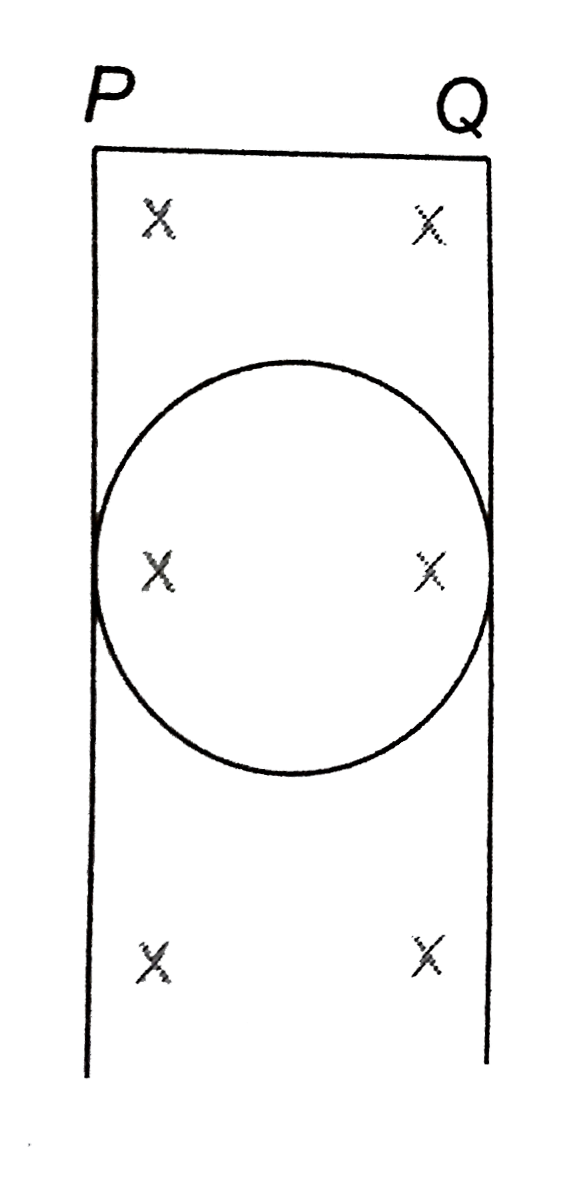
View SolutionA vertical ring of radius r and resistance on R falls vertically. It is in contact with two vertical rails which are joined at the top. The rails are without friction and resistance. There is a horizontal uniform, magnetic field of magnitude B perpendicular to the plane of the ring and the rails. When the speed of the ring is v , the current in the section PQ is

View Solution
