The value of γ=CP/CV is 4/3 for an adaibatic process of an ideal gas for which internal energy U=K+nPV. Find the value of n (K is constant) :
The correct Answer is:3
PVγ= constant
PV4/3= constant
In (V4)+In(P3)= constant
4(dVV)=−3(dPP)
4P(dV)+3V(dP)=0
3(PdV+VdP)+PdV=0
For adiabatic process, dQ=0=dU+dW
dU+PdV
Compare Eps. (i) (ii), dU=3(PdV+VdP)
U=K+3PV
So, n=3
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Comprehension56videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type9videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
Similar Questions
The internal energy of an ideal gas is sum of total kinetic energy of molecules. Consider an ideal gas in which the relation among U, P and V is U=2+3PVThe gas is
View SolutionFor an ideal gas the ratio of specific heats is CpCv=γ. The gas undergoes a polytropic process PV^(n) = a constant. Find the values of n for which the temperature of the gas increases when it rejects heat to the surrounding.
View Solution
Knowledge Check
- Question 1 - Select One
The value of γ=CP/Cv is 4/3 for an adiabatic process of an ideal gas for which internal energy U=A+BPV. The value of B will be (A is a constant)
A2B3C4D5 - Question 2 - Select One
P-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
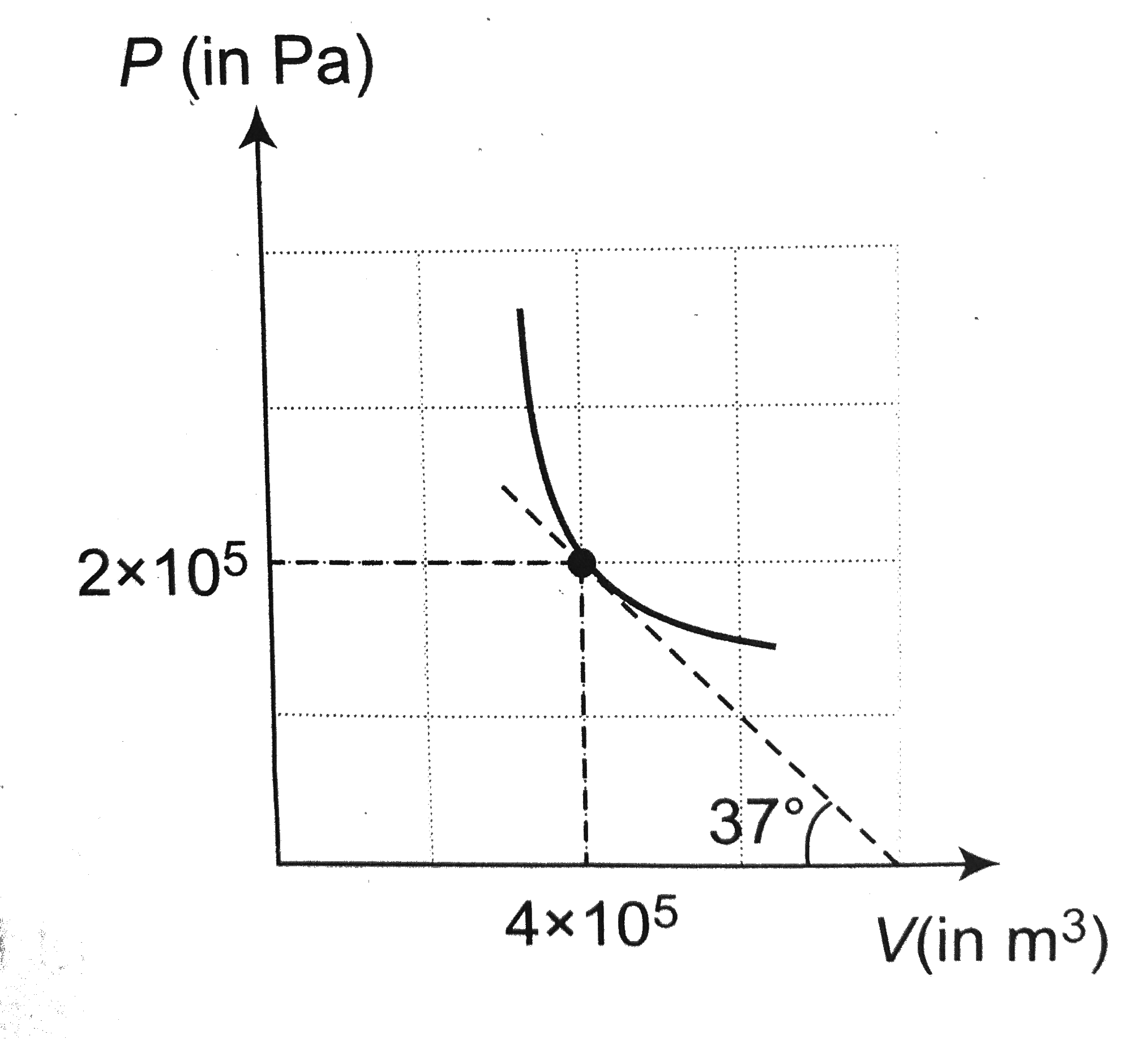 A34B−32C53D32
A34B−32C53D32 - Question 3 - Select One
In previous, Find the value of γ=CP/Cv:
A1.6B1.5C1.6D1.66
An ideal gas (CpCv=γ) is taken through a process in which the pressure and volume vary as (p=aVb. Find the value of b for which the specific heat capacity in the process is zero.
View SolutionThe relation between internal energy U, pressure P and volume V of a gas in an adiabatic process is
U=a+bPV where a and b are constant . What is the effective value of adiabatic constant γ.View SolutionThe relation between U, p and V for an ideal gas in an adiabatic process is given by relation U=a+bpV. Find the value of adiabatic exponent (γ) of this gas.
View SolutionAn ideal gas with adiabatic exponent γ=43 undergoes a process in which internal energy is related to volume as U=V2 . Then molar heat capacity of the gas for the process is :
View SolutionAn ideal gas with adiabatic exponent (γ=1.5) undergoes a process in which work done by the gas is same as increase in internal energy of the gas. Here R is gas constant. The molar heat capacity C of gas for the process is:
View Solution

