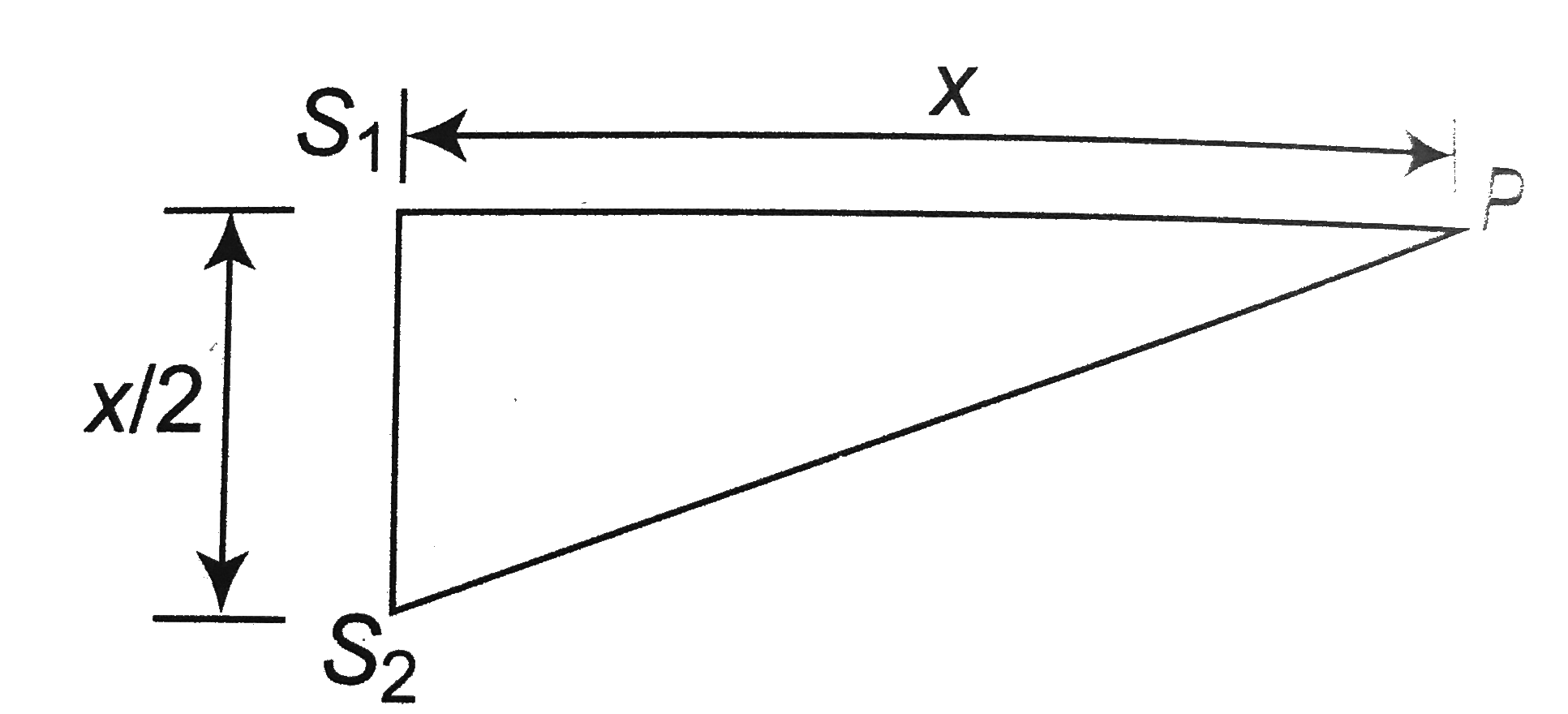
The wavelength of the waves arriving at P from two coherent sources $S_{1}$ and $S_{2}$ is 4m, while intensity of each wave is $I_{0}$ . The resultant intensity at $P$ is $2 I_{0}$ . Find the minimum value of $S_{2} P$

A

$\frac{x \sqrt{5}}{2}$

B

$2 x$

C

$(x + 1)$

D

$(x + \sqrt{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$I = I_{0} + I_{0} + 2 \sqrt{I_{0} . I_{0}} cos ϕ = 2 I_{0}$
so $cos ϕ = 0$
$ϕ = \frac{n π}{2} = \frac{π}{2}$
( $n = 1$ for $S_{2} P$ to be minimum)
$ϕ = (\frac{2 π}{λ}) Δ x = (\frac{2 π}{4}) Δ x \frac{π}{2}$
$Δ x = 1 m$
$Δ x = S_{2} P - S_{1} P = 1$
$S_{2} P = S_{1} P + 1 = (x + 1)$ metres
thus the detector should be placed at a distance of 3 m from the source. Note that there is no abrupt phase change.

|

Updated on:21/07/2023

Class 11 PHYSICS SOUND WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

The wavelength of the waves arriving at P from two coherent sources $S_{1}$ and $S_{2}$ is 4m, while intensity of each wave is $I_{0}$ . The resultant intensity at $P$ is $2 I_{0}$ . Find the minimum value of $S_{2} P$
A $\frac{x \sqrt{5}}{2}$
B $2 x$
C $(x + 1)$
D $(x + \sqrt{2})$
Question 2 - Select One

In the figure the intensity of waves arriving at D from two coherent sources $S_{1}$ and $S_{2}$ is $I_{0}$ The wavelength of the wave is $λ = 4 m$ . Resultant intensity at D will be:
A $4 I_{0}$
B $I_{0}$
C $2 I_{0}$
Dzero
Question 3 - Select One
In the figure , the intensity of waves arriving at D from two coherent soucrces $s_{1} and s_{2} i s I_{0}$ . The wavelength of the wave is $λ = 4 m$ . Resultant intensity at D will be

A $4 l_{0}$
B $l_{0}$
C $2 l_{0}$
Dzero

A2Z-WAVES AND ACOUSTICS-Superposition And Interference

Home
Ask Doubt
Profile