The (x,y) co-ordinates of the corners of a square plate are (0,0),(L,0), (L,L) and (0,L). The edges of the plate are clamped and transverse standing waves are set up in it. If u(x,y) denotes the displacement of the plate at the point (x,y) at some instant of time, the possible expression (s) for u is (are) (a=positiveconstant)
acos(πr/2L)cos(πy/2L)
asin(πx/L)sin(πy/L)
asin(πx/L)sin(2πy/L)
acos(2πx/L)sin(πy/L)
The correct Answer is:B, C
To solve the problem of finding the possible expressions for the displacement u(x,y) of a square plate with clamped edges, we need to analyze the boundary conditions and the nature of standing waves.
1. Understand the Boundary Conditions:
- The edges of the square plate are clamped. This means that the displacement u(x,y) must be zero at the edges. The corners of the square plate are given as:
- (0,0)
- (L,0)
- (L,L)
- (0,L)
2. Identify the Edges:
- The edges of the square plate can be represented as:
- Bottom edge: y=0 for 0≤x≤L
- Right edge: x=L for 0≤y≤L
- Top edge: y=L for 0≤x≤L
- Left edge: x=0 for 0≤y≤L
3. Formulate the Displacement Function:
- The displacement function u(x,y) must satisfy the boundary conditions u(x,0)=0, u(x,L)=0, u(0,y)=0, and u(L,y)=0.
4. Examine Possible Forms of u(x,y):
- A general form for the displacement in terms of sine functions is:
u(x,y)=Asin(nπxL)sin(mπyL)
- Here, n and m are positive integers, which ensure that the displacement is zero at the boundaries.
5. Evaluate the Given Options:
- Option A: u(x,y)=Acos(πx2L)cos(πy2L)
- At x=0 and y=0, u(0,0)=A (not zero). This option is not valid.
- Option B: u(x,y)=Asin(πxL)sin(πyL)
- At x=0, u(0,y)=0 and at y=0, u(x,0)=0. This option is valid.
- Option C: u(x,y)=Asin(πxL)sin(2πyL)
- At x=0, u(0,y)=0 and at y=0, u(x,0)=0. This option is valid.
- Option D: u(x,y)=Acos(2πxL)sin(πyL)
- At x=0, u(0,y)=A (not zero). This option is not valid.
6. Conclusion:
- The valid expressions for the displacement u(x,y) are:
- Option B: Asin(πxL)sin(πyL)
- Option C: Asin(πxL)sin(2πyL)
Final Answer:
The possible expressions for u(x,y) are:
- u(x,y)=Asin(πxL)sin(πyL)
- u(x,y)=Asin(πxL)sin(2πyL)
- The edges of the square plate are clamped. This means that the displacement u(x,y) must be zero at the edges. The corners of the square plate are given as:
- (0,0)
- (L,0)
- (L,L)
- (0,L)
- The edges of the square plate can be represented as:
- Bottom edge: y=0 for 0≤x≤L
- Right edge: x=L for 0≤y≤L
- Top edge: y=L for 0≤x≤L
- Left edge: x=0 for 0≤y≤L
- The displacement function u(x,y) must satisfy the boundary conditions u(x,0)=0, u(x,L)=0, u(0,y)=0, and u(L,y)=0.
- A general form for the displacement in terms of sine functions is:
u(x,y)=Asin(nπxL)sin(mπyL)
- Here, n and m are positive integers, which ensure that the displacement is zero at the boundaries.
- Option A: u(x,y)=Acos(πx2L)cos(πy2L)
- At x=0 and y=0, u(0,0)=A (not zero). This option is not valid.
- Option B: u(x,y)=Asin(πxL)sin(πyL)
- At x=0, u(0,y)=0 and at y=0, u(x,0)=0. This option is valid.
- Option C: u(x,y)=Asin(πxL)sin(2πyL)
- At x=0, u(0,y)=0 and at y=0, u(x,0)=0. This option is valid.
- Option D: u(x,y)=Acos(2πxL)sin(πyL)
- At x=0, u(0,y)=A (not zero). This option is not valid.
- The valid expressions for the displacement u(x,y) are:
- Option B: Asin(πxL)sin(πyL)
- Option C: Asin(πxL)sin(2πyL)
The possible expressions for u(x,y) are:
- u(x,y)=Asin(πxL)sin(πyL)
- u(x,y)=Asin(πxL)sin(2πyL)
Topper's Solved these Questions
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Comprehension
12 Videos
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Integer
4 Videos
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Single Correct
51 Videos
- ARCHIVES 1 VOLUME 6BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 1 VOLUME 6EXERCISE - Integer
4 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
Similar Questions
The (x,y) co-ordinates of the corners of a square plate are (0,0), (L,L) and (0,L). The edges of the plate are clamped and transverse standing waves are set up in it. If u(x,y) denotes the displacement of the plate at the point (x,y) at some instant of time, the possible expression (s) for u is (are) (a=positiveconstant)
View SolutionFor a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
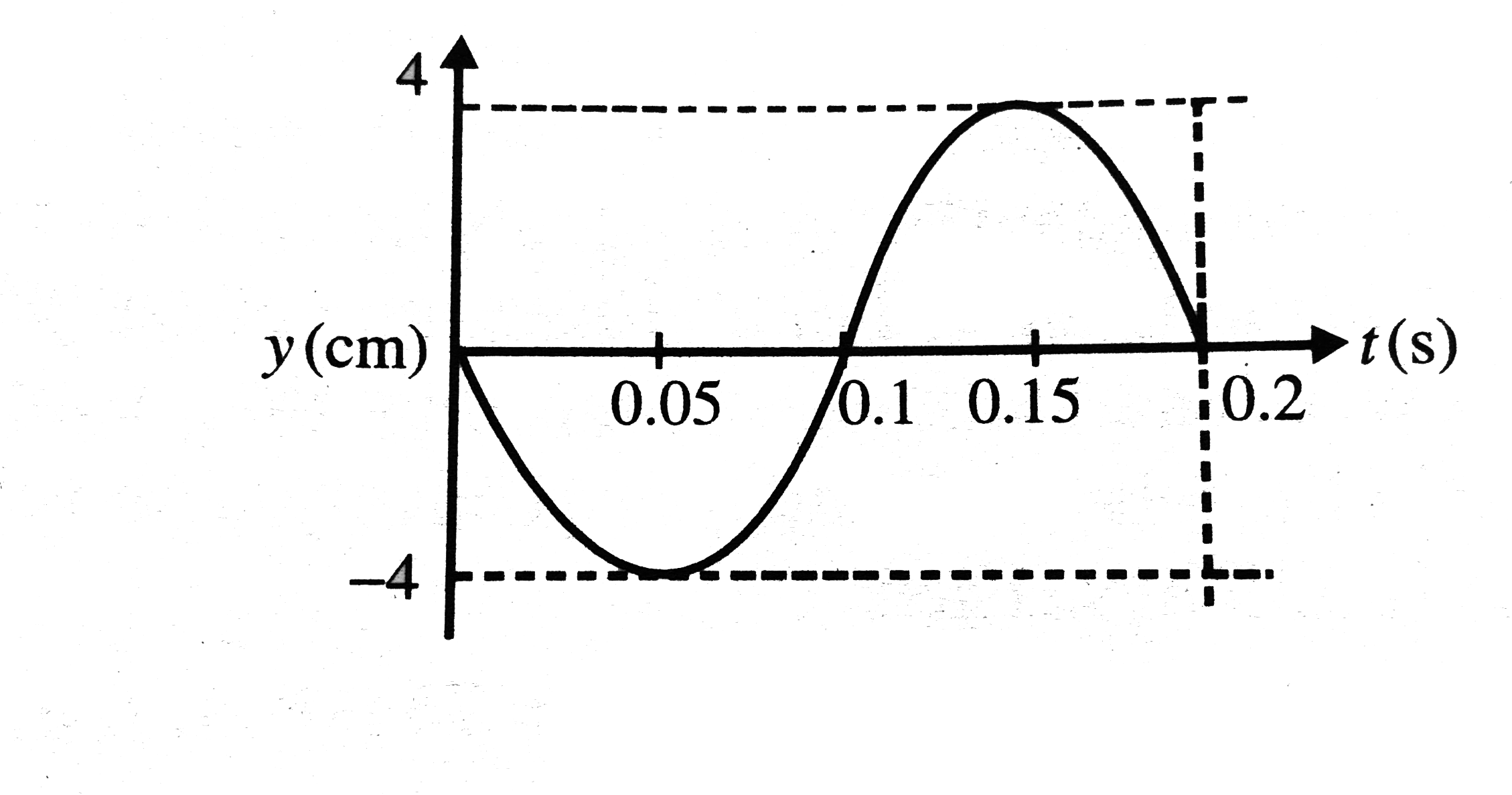
View Solution
Knowledge Check
If the corner points of the feasible region for an L.P.P. are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5), then the minimum value of the objective function F=4x+6y occurs at
AA) (0, 2) onlyBB) (3, 0) onlyCC) the mid-point of the line segment joining the point (0, 2) and (3, 0) onlyDD) every point on the line segment joining the point (0, 2) and (3, 0)If the objective function for a L.P.P. is Z=5x+7y and the corner points of the bounded feasible region are (0, 0), (7, 0), (3, 4) and (0, 2), then the maximum value of Z occurs at
AA) (0, 0)BB) (7, 0)CC) (3, 4)DD) (0, 2)
For a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
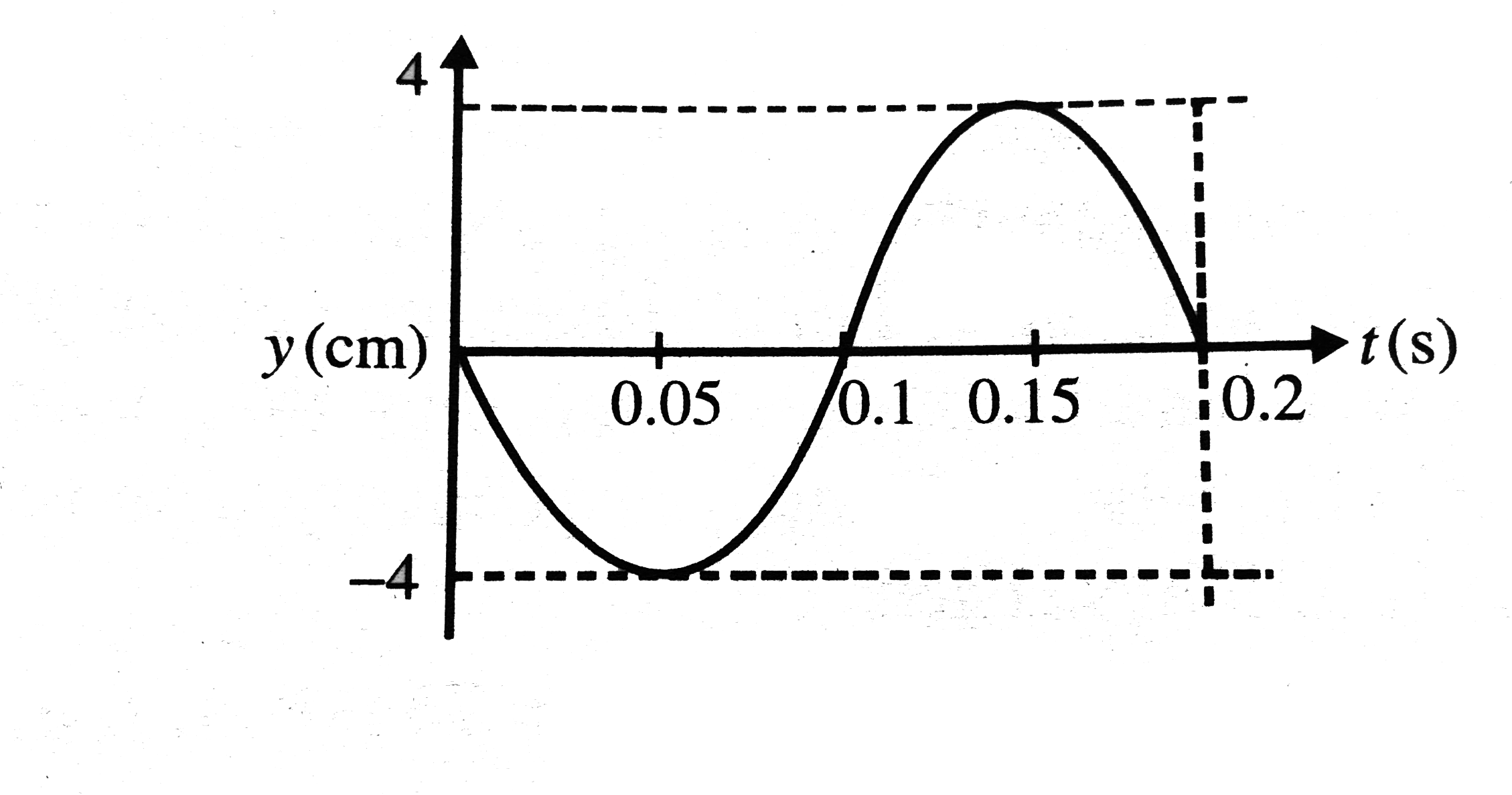
View SolutionThe figure shows an isosceles triangle plate of mass M and base L.
The angle at the apex is 90∘. The apex lies at the origin and the base is parallel to X−axis.
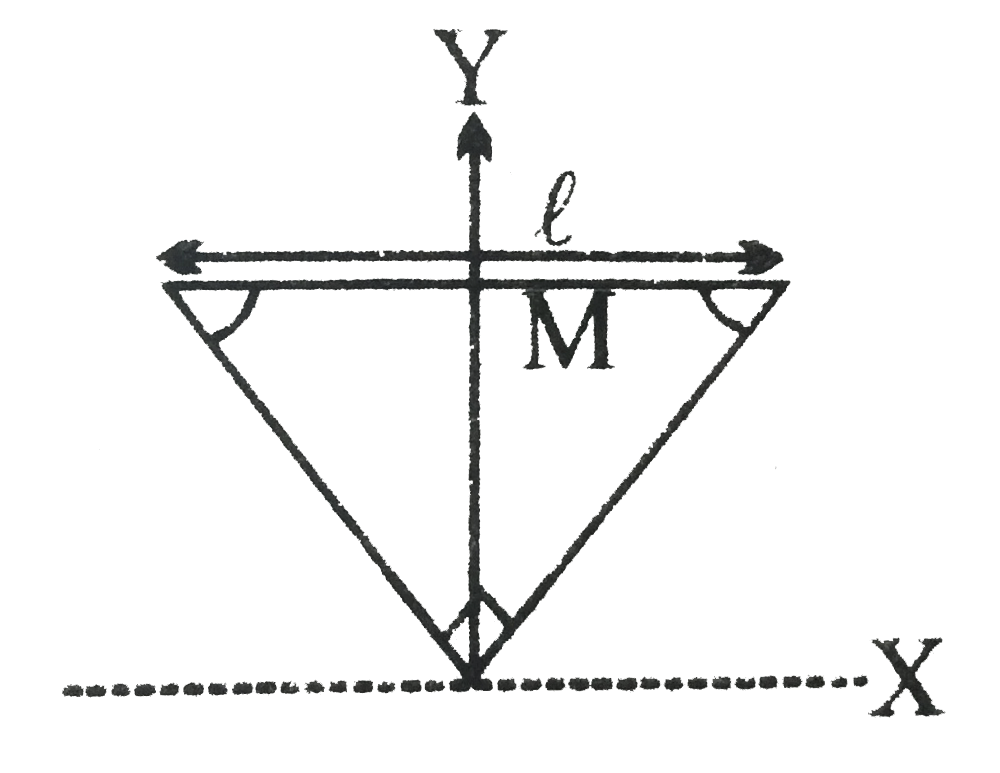
The moment of inertia of the plate about the y−axis is
View SolutionFind the equation of the straight line through the point (α,β) and perpendiculasr to the line lx+my+n=0.
View SolutionThe standing wave in a medium is expressed as y=0.2sin(0.8x)cos(3000t)m. The distance between any two consecutive points of minimum of maximum displacement is
View SolutionA dielectric slab is introduced inside an uncharged capacitor of plate area A and plate separation L. The surface area of the slab is A and its thickness is slightly less than L. Let the surfaces of the slab that are facing the plates of the capacitor be called its two “faces”. The dielectric constant of the slab varies with distance x from one of its faces as: K=K0(1+XL), where K0 is a constant. After the insertion of the slab, the capacitance of the capacitor is n(K0ε0ALloge2). The value of n is _________.
View Solutionx and y co-ordinates of a particle moving in x−y plane at some instant of time are x=2t and y=4t.Here x and y are in metre and t in second. Then
The distance travelled by the particle in a time from t=0 to t=2s is ………m
View Solution
