There are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
The correct Answer is:6
To solve the problem, we need to calculate the potential difference VA−VC between the shells A and C, given the conditions of the concentric shells and their charges.
1. Identify the Shells and Their Charges:
- Shell A has radius a.
- Shell B has radius 2a and charge +q.
- Shell C has radius 3a and is earthed (potential is set to zero).
- Shell D has radius 4a and charge −q.
2. Understand the Effect of Earthing Shell C:
- When shell C is earthed, its potential VC becomes zero.
3. Use Gauss's Law to Determine Electric Fields:
- For the region between shells A and B (from r=a to r=2a), the electric field E is zero because the charge enclosed is zero.
- From shell B to shell C (from r=2a to r=3a), the electric field can be calculated using Gauss's Law:
E=kqr2
where k=14πϵ0.
4. Calculate the Potential Difference VA−VC:
- The potential difference can be expressed as:
VA−VC=−∫rCrAEdr
- Here, rA=a and rC=3a. The potential difference can be split into two parts:
VA−VC=−∫2aa0dr−∫3a2akqr2dr
- The first integral evaluates to zero since the electric field is zero between shells A and B.
5. Evaluate the Second Integral:
- The second integral becomes:
−∫3a2akqr2dr=−kq(−1r)3a2a
- Evaluating this gives:
−kq(−13a+12a)=kq(12a−13a)
- Finding a common denominator (6a):
=kq(36a−26a)=kq6a
6. Final Result:
- Therefore, the potential difference VA−VC is:
VA−VC=kq6a
Conclusion:
The potential difference VA−VC is kq6a.
- Shell A has radius a.
- Shell B has radius 2a and charge +q.
- Shell C has radius 3a and is earthed (potential is set to zero).
- Shell D has radius 4a and charge −q.
- When shell C is earthed, its potential VC becomes zero.
- For the region between shells A and B (from r=a to r=2a), the electric field E is zero because the charge enclosed is zero.
- From shell B to shell C (from r=2a to r=3a), the electric field can be calculated using Gauss's Law:
E=kqr2
where k=14πϵ0.
- The potential difference can be expressed as:
VA−VC=−∫rCrAEdr
- Here, rA=a and rC=3a. The potential difference can be split into two parts:
VA−VC=−∫2aa0dr−∫3a2akqr2dr
- The first integral evaluates to zero since the electric field is zero between shells A and B.
- The second integral becomes:
−∫3a2akqr2dr=−kq(−1r)3a2a
- Evaluating this gives:
−kq(−13a+12a)=kq(12a−13a)
- Finding a common denominator (6a):
=kq(36a−26a)=kq6a
- Therefore, the potential difference VA−VC is:
VA−VC=kq6a
The potential difference VA−VC is kq6a.
Topper's Solved these Questions
Similar Questions
Four concentric conducting spherical shells A, B, C and D of radii a, 2a, 3a and 4a respectively. Shell B and D are given charges q and −q respectively. If shell C is grounded then potential difference (VA — VC) is
View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b, and c. The shells A and C are given charge q and -q, respectively, and shell B is earthed. Then,
View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.

View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.

View SolutionThree concentric spherical conductors A, B, and C of radii r, 2R, and 4R, respectively. A and C is shorted and B is uniformly charged (charge +Q).
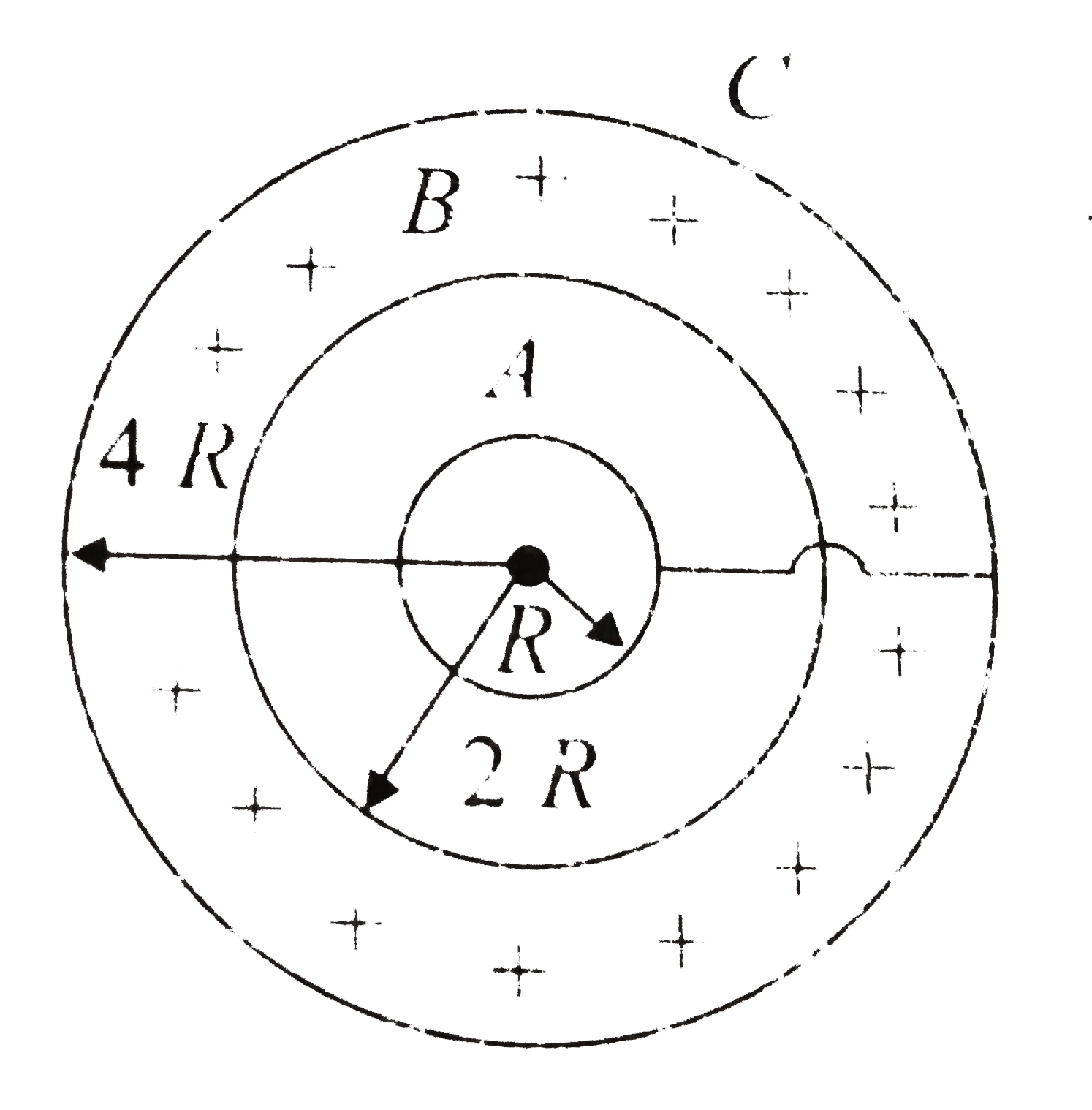
Potential at B is
View SolutionThree concentric spherical conductors A, B, and C of radii r, 2R, and 4R, respectively. A and C is shorted and B is uniformly charged (charge +Q).
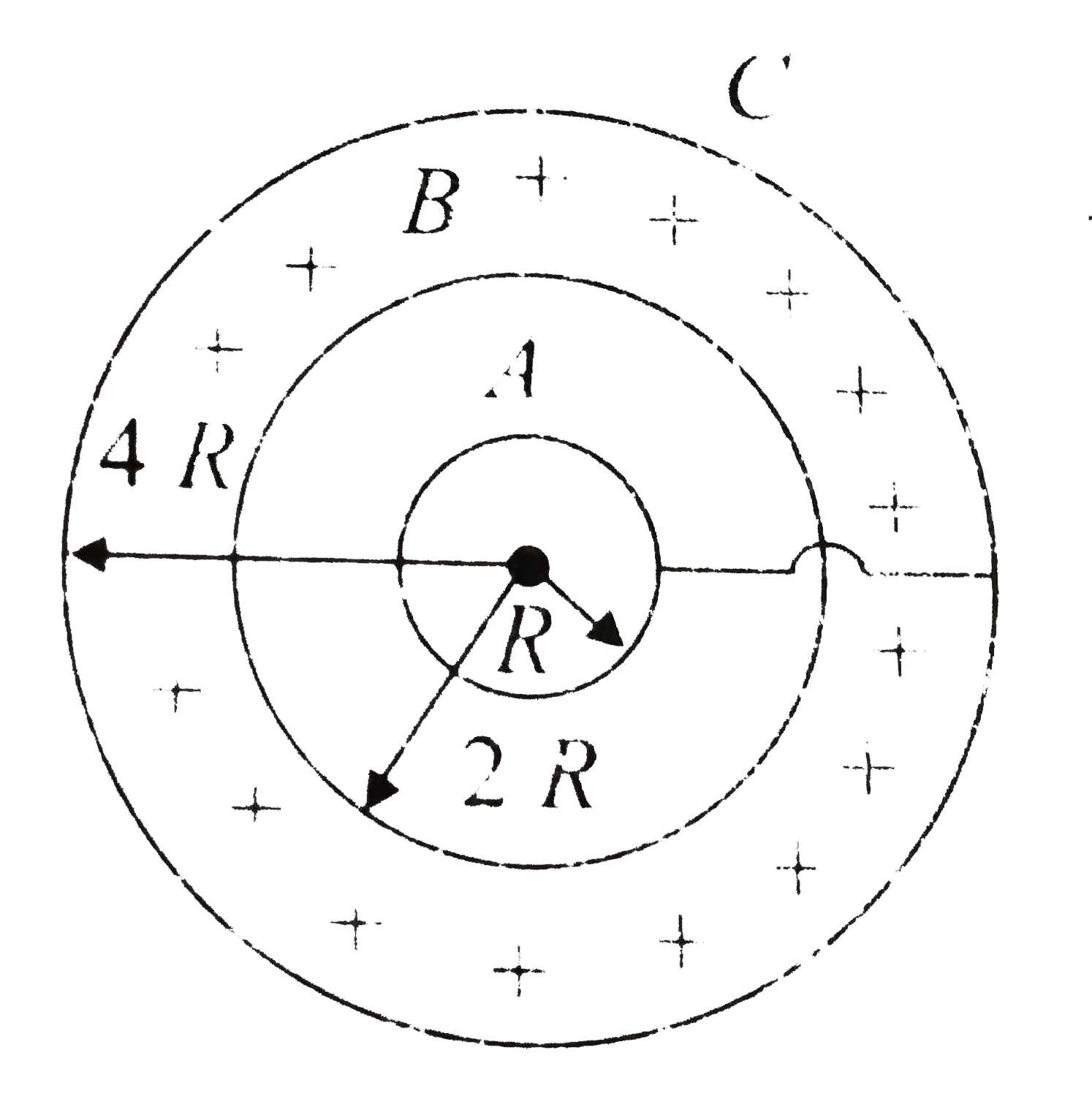
Potential at A is
View SolutionFigure shows a system of three concentric metal shells, A, B and C with radii a, 2a and 3a respectively. Shell B is earthed and shell C is given a charge Q. Now if shell C is connected to shell A, then find the final charge on the shell B

View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionTwo concentric spherical conducting shells of radii 'a' and 2a are initially given charges +2Q and +Q respectively as shown. The total heat dissipated after switch 'S' has been closed is (where k=14πε0)

View SolutionThere are two concentric conducting spherical shells of radius rA and rB respectively (rB=2rA). If the inner shell is given a charge Q and outer shell is given a charge 2Q, then the potential difference between the surfaces of the shells will be K=14πε0
View Solution