Match the following
Table - 1Table - 2(A)σ2/ε0(P)C2/J−m(B)ε0(Q)Farad(C)ampere - secondVolt(R)J/m3(D)VE(S)metre
The correct Answer is:(A)R,(B)P,(C)Q,(D)S
To solve the matching question between Table 1 and Table 2, we will analyze the units provided in Table 1 and find their corresponding matches in Table 2.
1. Identify the Units in Table 1:
- (A) σ2ϵ0
- (B) ϵ0
- (C) ampere⋅secondVolt
- (D) VE
2. Match (D) VE:
- The unit VE can be interpreted as VoltageElectric Field.
- From the relationship V=E⋅L, we can deduce that VE=L, where L is a length.
- Therefore, D matches with S (metre).
3. Match (C) ampere⋅secondVolt:
- The unit ampere⋅secondVolt can be rewritten as I⋅TV.
- This can be interpreted as charge Q (since Q=I⋅T) divided by potential V.
- The unit of capacitance is Farad, which is defined as CV.
- Thus, C matches with Q (Farad).
4. Match (B) ϵ0:
- The permittivity of free space ϵ0 can be derived from the equation F=14πϵ0Q1Q2R2.
- Rearranging gives ϵ0=Q24πFR2.
- The unit of ϵ0 can be expressed in terms of charge (Coulombs) and force (Newtons), leading to Farad (since Farad=CV).
- Therefore, B matches with P (Farad).
5. Match (A) σ2ϵ0:
- The surface charge density σ has units of Cm2.
- Thus, σ2 has units of C2m4.
- Dividing by ϵ0 (which has units of C2N⋅m2), we get C2/m4C2/(N⋅m2)=Nm2.
- This is equivalent to J/m3 (Joules per cubic meter).
- Therefore, A matches with R (J/m³).
Final Matches:
- (A) σ2ϵ0 → R (J/m³)
- (B) ϵ0 → P (Farad)
- (C) ampere⋅secondVolt → Q (Farad)
- (D) VE → S (metre)
Summary of Matches:
- A → R
- B → P
- C → Q
- D → S
- (A) σ2ϵ0
- (B) ϵ0
- (C) ampere⋅secondVolt
- (D) VE
- The unit VE can be interpreted as VoltageElectric Field.
- From the relationship V=E⋅L, we can deduce that VE=L, where L is a length.
- Therefore, D matches with S (metre).
- The unit ampere⋅secondVolt can be rewritten as I⋅TV.
- This can be interpreted as charge Q (since Q=I⋅T) divided by potential V.
- The unit of capacitance is Farad, which is defined as CV.
- Thus, C matches with Q (Farad).
- The permittivity of free space ϵ0 can be derived from the equation F=14πϵ0Q1Q2R2.
- Rearranging gives ϵ0=Q24πFR2.
- The unit of ϵ0 can be expressed in terms of charge (Coulombs) and force (Newtons), leading to Farad (since Farad=CV).
- Therefore, B matches with P (Farad).
- The surface charge density σ has units of Cm2.
- Thus, σ2 has units of C2m4.
- Dividing by ϵ0 (which has units of C2N⋅m2), we get C2/m4C2/(N⋅m2)=Nm2.
- This is equivalent to J/m3 (Joules per cubic meter).
- Therefore, A matches with R (J/m³).
- (A) σ2ϵ0 → R (J/m³)
- (B) ϵ0 → P (Farad)
- (C) ampere⋅secondVolt → Q (Farad)
- (D) VE → S (metre)
- A → R
- B → P
- C → Q
- D → S
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
Match the following
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣Table-1Table-2(A)Stress×Strain(P)J(B)YAl(Q)N/m(C)Yl3(R)J/m3(D)FlAY(S)m∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionMatch the following
Table-1Table-2(A)L(P)[M0L0T−2](B)Magnetic Flux(Q)[ML2T−2A−1](C)LC(R)[ML2T−2A−2](D)CR2(S)None
View SolutionMatch the following.
∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣Table-1Table-2(A)Coefficient of viscosity(P)[M2L−1T−2](B)Surface tension(Q)[ML0T−2](C)Modulus of elasticity(R)[ML−1T−2](D)Energy per unit volume(S)Noneof a fiuid∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionMatch the following :
Column-IColumn-II(A)3s1(p)n=3(B)3p1(q)l=0(C)4s1(r)l=1(D)4d1(s)m=0(t)m=±1
View SolutionComparing L-C oscillation with the oscillation if spring-block-system, match the following table.
Comparing L-C oscillations with the oscillations of spring-block sytem, match the following table Table-1(LC oscillations)Table-2(Spring-block oscillations)(A)L(P)k(B)C(Q)m(C)i(R)v(D)didt(S)x(T)None
View SolutionIn L-C-R series circuit suppose ωr is resonance frequency, then match the following table,
Table-1Table-2(A)If ω>ωr(P)Current will lead the voltage(B)If ω=ωr(Q)Voltage will lead the current(C)If ω=2ωr(R)XL=2XC(D)If ω<ωr(S)Current and voltage are in phase(T)None
View SolutionMatch the following

PQRS(A)1243(B)2143(C)4132(D)4321
View SolutionMatch the following
∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣ Table-1 Table-2(A) Steel(P) Young's modulus of elasticity(B) Water(Q) Bulk modulus of elasticity(C) Hydrogen gas filled(R) sheer modulus of in a chamber elasticity∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionIn the diagram shown in figure mass of both the balls in same. Match the following columns.
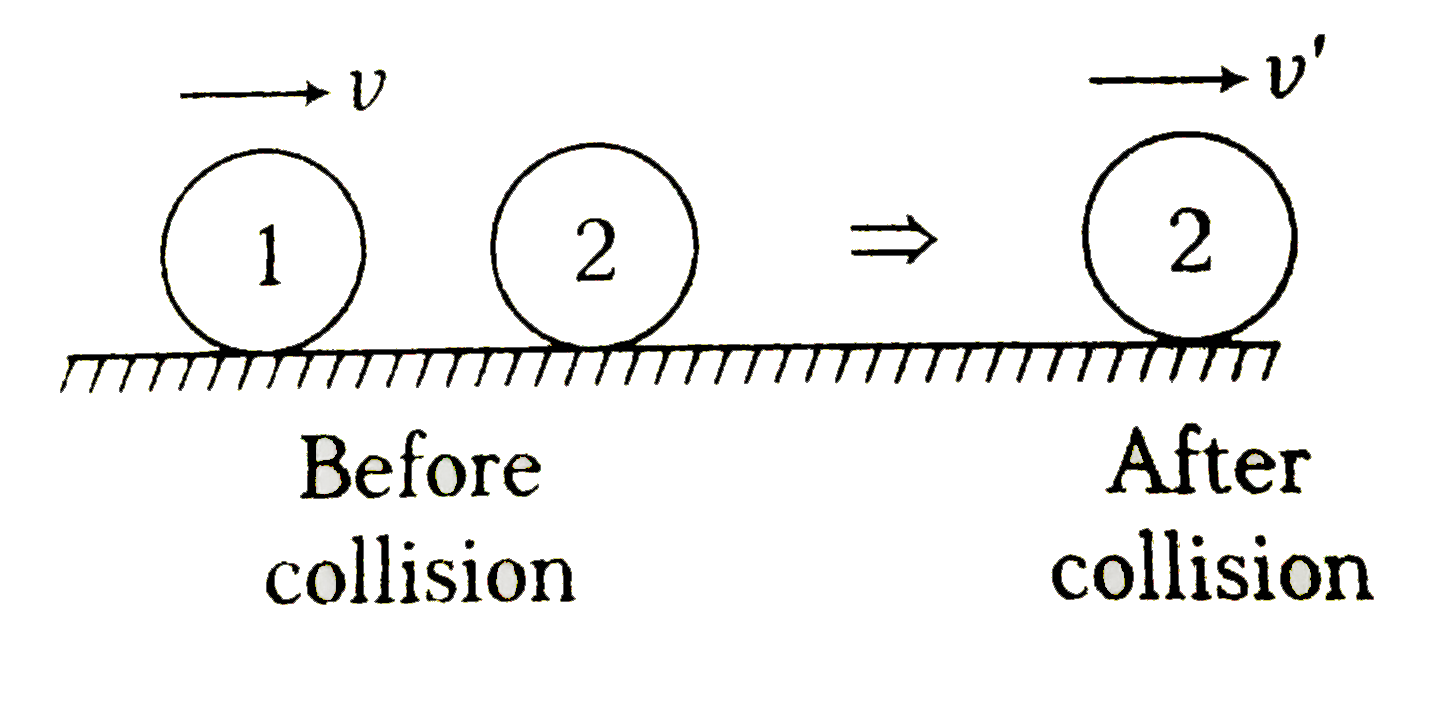
Column1Column2A Forv′=vP e=0B Forv′=v/2Q e=1C Forv′=3/4vR e=1/2-(S data is insufficient
View SolutionFind the equations of the planes that passes through three points. (a) (b)(c)((d)(e)1, 1, 1(f)), ((g)(h)6, 4, 5(i)), ((j)(k) 4, 2, 3(l))(m) (n) (o) ( p ) (q)(( r ) (s)1," "1," "0( t ))," "((
View Solution
