There are four solid balls with their centres at the four corners of a square of side a. the mass of each sphere is m and radius is r. Find the moment of inertia of the system about one of the sides of the square
85mr2+2ma2
58mr2+2ma2
85mr2+ma2
85mr2+4ma2
To find the moment of inertia of the system of four solid balls located at the corners of a square about one of the sides of the square, we can follow these steps:
Step 1: Understand the Configuration
We have four solid balls, each with mass m and radius r, located at the corners of a square with side length a. We need to find the moment of inertia about one of the sides of the square, say side AA'.
Step 2: Identify the Moment of Inertia of One Ball
The moment of inertia I of a solid sphere about its own center is given by the formula:
I=25mr2
where m is the mass of the sphere and r is its radius.
Step 3: Calculate the Moment of Inertia for Each Ball
Since we are calculating the moment of inertia about the axis AA', we need to consider the contributions from each of the four balls.
- Ball 1 (at corner A): This ball is on the axis, so its moment of inertia about AA' is:
I1=25mr2
- Ball 2 (at corner B): This ball is at a distance a from the axis AA'. Using the parallel axis theorem, we have:
I2=25mr2+ma2
- Ball 3 (at corner C): This ball is at a distance a from the axis AA' (same reasoning as Ball 2):
I3=25mr2+ma2
- Ball 4 (at corner D): This ball is at the same distance a from the axis AA' (same reasoning as Ball 2):
I4=25mr2+ma2
Step 4: Sum the Moments of Inertia
Now, we can sum the moments of inertia of all four balls to find the total moment of inertia about the axis AA':
IAA′=I1+I2+I3+I4
Substituting the values we found:
IAA′=25mr2+(25mr2+ma2)+(25mr2+ma2)+(25mr2+ma2)
IAA′=25mr2+3(25mr2+ma2)
IAA′=25mr2+65mr2+3ma2
IAA′=85mr2+3ma2
Final Result
Thus, the moment of inertia of the system about one of the sides of the square is:
IAA′=85mr2+3ma2
We have four solid balls, each with mass m and radius r, located at the corners of a square with side length a. We need to find the moment of inertia about one of the sides of the square, say side AA'.
The moment of inertia I of a solid sphere about its own center is given by the formula:
I=25mr2
where m is the mass of the sphere and r is its radius.
Since we are calculating the moment of inertia about the axis AA', we need to consider the contributions from each of the four balls.
I1=25mr2
I2=25mr2+ma2
I3=25mr2+ma2
I4=25mr2+ma2
Now, we can sum the moments of inertia of all four balls to find the total moment of inertia about the axis AA':
IAA′=I1+I2+I3+I4
Substituting the values we found:
IAA′=25mr2+(25mr2+ma2)+(25mr2+ma2)+(25mr2+ma2)
IAA′=25mr2+3(25mr2+ma2)
IAA′=25mr2+65mr2+3ma2
IAA′=85mr2+3ma2
Thus, the moment of inertia of the system about one of the sides of the square is:
IAA′=85mr2+3ma2
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.24videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.34videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example1videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
Four spheres of diameter 2a and mass M are placed with their centres on the four corners of a square of side b. Then moment of inertia of the system about an axis about one of the sides of the square is :-
View SolutionFour spheres A, B, C, D, each of mass m and diameter 2 a are placed with their centres at die four corners of a square of side b. What is the moment of inertia of the system about any side of the square ?
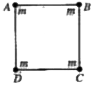 View Solution
View SolutionFour solid sphereas each of diameter √5cm and mass 0.5kg are placed with their centres at the corners of a square of side 4cm. The moment of inertia of the system about the diagonal of the square is N×10−4kg−m2, the N is -
View SolutionFour thin rods each of mass m and length l are joined to make a square. Find moment of inertia of all the four rods about any side of the square.
View SolutionA square frame is made rods each of mass m and length l. The moment of inertia of the square about its face diagonal is
View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.
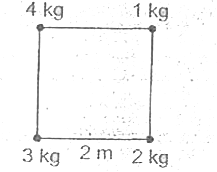 View Solution
View SolutionFour solid spheres, each of mass (m) and diameter (d) are stuck together such that the lines joining the centres form a square of side length (d). The ratio of I0 & IA , where I0 is the moment of inertia of the system about an axis through the centre of the square and IA is moment of inertia of the system about the centre of any one of the spheres, is equal to (both axes are perpendicular to plane of paper)
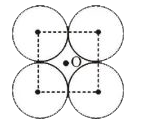 View Solution
View SolutionFour solid spheres, each of mass (m) and diameter (d) are stuck together such that the lines joining the centres form a square of side length (d). The ratio of I0 & IA , where I0 is the moment of inertia of the system about an axis through the centre of the square and IA is moment of inertia of the system about the centre of any one of the spheres, is equal to (both axes are perpendicular to plane of paper)
 View Solution
View SolutionFour identical particles each of mass m are arranged at the corners of a square of sie a. If mass of one of th particle is doubled, the shift in the centre of mass of the system is
View SolutionFour particles each of mass 'm' are kept at the four corners of a square of edge 'a'. Find the moment of inertia of the system about a line perpendicular to the plane of the square and passing through the center of the square.
View Solution

