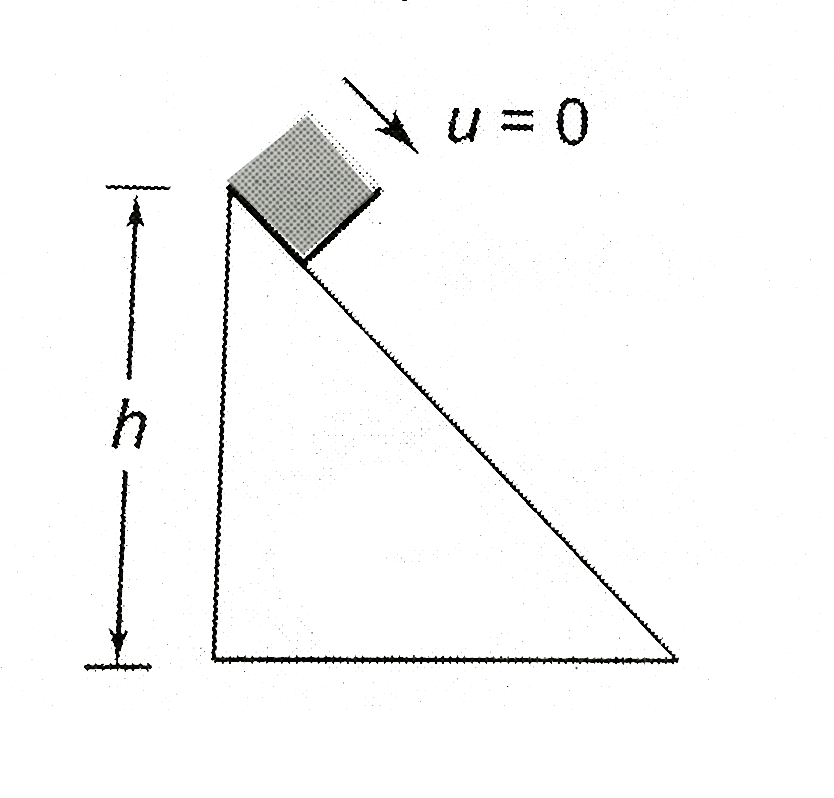There are two inclined planes A and B of same dimensions. A is sufficiently rough but B is smooth A round shaped object is released from rest at the top point of inclined plane A and acceleration the object is found to be a, and v1 is the velocity of centre of object when it reaches the bottom. When the same process is repeated with B then corresponding values are found to be a2andv2.
a1>a2
a1<a2
v1>v2
v1<v2
The correct Answer is:B, D
To solve the problem, we will analyze the motion of a round-shaped object on two inclined planes, A (rough) and B (smooth). We will determine the relationship between their accelerations and final velocities.
1. Understanding the System:
- We have two inclined planes, A and B, with the same dimensions (height and angle).
- Plane A is rough, allowing the object to roll without slipping, while plane B is smooth, causing the object to slide without rolling.
2. Acceleration on Plane A (Rough):
- For the rough inclined plane A, the object rolls down. The acceleration a1 can be calculated using the formula:
a1=gsinθ1+ImR2
where I is the moment of inertia of the object, m is its mass, R is its radius, and g is the acceleration due to gravity.
3. Acceleration on Plane B (Smooth):
- For the smooth inclined plane B, the object slides down without rolling. The acceleration a2 is given by:
a2=gsinθ
4. Comparing Accelerations:
- Since a1 includes a term in the denominator that is greater than 1 (due to the moment of inertia), we can conclude:
a1<a2
5. Velocity at the Bottom of Plane A:
- The final velocity v1 of the object when it reaches the bottom of plane A can be found using energy conservation:
mgh=12mv21+12Iω2
Since ω=v1R, we can substitute and rearrange to find v1.
6. Velocity at the Bottom of Plane B:
- For plane B, the final velocity v2 is calculated similarly:
mgh=12mv22
This simplifies to:
v2=√2gh
7. Comparing Velocities:
- Since part of the potential energy on plane A is converted into rotational kinetic energy, less energy is available for linear motion compared to plane B. Thus:
v1<v2
Conclusion:
- We find that:
- a1<a2 (the acceleration on the rough plane is less than that on the smooth plane).
- v1<v2 (the final velocity on the rough plane is less than that on the smooth plane).
Final Answers:
- a1<a2
- v1<v2
- We have two inclined planes, A and B, with the same dimensions (height and angle).
- Plane A is rough, allowing the object to roll without slipping, while plane B is smooth, causing the object to slide without rolling.
- For the rough inclined plane A, the object rolls down. The acceleration a1 can be calculated using the formula:
a1=gsinθ1+ImR2
where I is the moment of inertia of the object, m is its mass, R is its radius, and g is the acceleration due to gravity.
- For the smooth inclined plane B, the object slides down without rolling. The acceleration a2 is given by:
a2=gsinθ
- Since a1 includes a term in the denominator that is greater than 1 (due to the moment of inertia), we can conclude:
a1<a2
- The final velocity v1 of the object when it reaches the bottom of plane A can be found using energy conservation:
mgh=12mv21+12Iω2
Since ω=v1R, we can substitute and rearrange to find v1.
- For plane B, the final velocity v2 is calculated similarly:
mgh=12mv22
This simplifies to:
v2=√2gh
- Since part of the potential energy on plane A is converted into rotational kinetic energy, less energy is available for linear motion compared to plane B. Thus:
v1<v2
- We find that:
- a1<a2 (the acceleration on the rough plane is less than that on the smooth plane).
- v1<v2 (the final velocity on the rough plane is less than that on the smooth plane).
- a1<a2
- v1<v2
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )
3 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
48 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Knowledge Check
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1A solid cylinder rolls down from an inclined plane of height h. What is the velocity of the cylinder when it reaches at the bottom of the plane ?
A√2gh3B√2ghC√4gh3D√3gh2A rolling body is released from rest on sufficient rough long inclined plane of inclination θ. Consider four points A, B, C and D on the sphere. After one revolution.
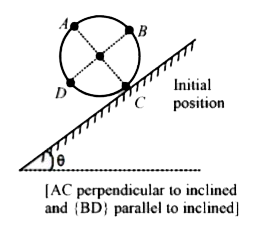 AAcceleration of point C is zero.BAcceleration of point B is along line BD.CAcceleration of point A is along line AC.DAcceleration of point C is along line CA.
AAcceleration of point C is zero.BAcceleration of point B is along line BD.CAcceleration of point A is along line AC.DAcceleration of point C is along line CA.
A solid cylinder and ring are released from rest in top of inclined plane. Find ratio of their velocities when they reach bottom,assuming pure rolling
View SolutionA block is released on an smooth inclined plane of inclination θ. After how much time it reaches to the bottom of the plane?
View SolutionA body is released from the top of a smooth inclined plane of inclination θ. It reaches the bottom with velocity v. If the angle of inclination is doubled for the same length of the plane, what will be the velocity of the body on reaching the ground
View SolutionA body is released from the top of a smooth inclined plane of inclination θ. It reaches the bottom with velocity v. If the angle of inclina-tion is doubled for the same length of the plane, what will be the velocity of the body on reach ing the ground .
View SolutionA solid sphere rolls down a smooth inclined plane of height h. If it stats from rest then the speed of the sphere when it reaches the bottom is given by
View Solution