A block of mass M has a circular cut with a frictionless surface as shown. The block rests on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at x = 0, in a co-ordinate system fixed to the table. A point mass m is released from rest at the topmost point of the path as shown and it slides down. When the mass loses contact with the block, its position is x and the velocity is v. At that instant, which of the following options is/are correct?
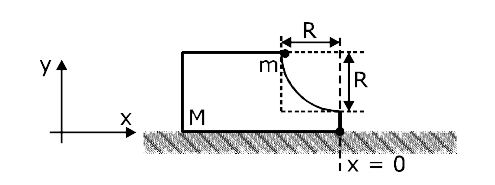
The velocity of the point mass m is : v= ⎷2gR1+mM
The x component of displacement of the centre of mass of the block M is : −mRM+m
The position of the point mass is: =−√2mRM+m
The velocity of the block M is V=−mM√2gR
The correct Answer is:A, B
If speed of the block is V, then using conservation of linear momentum
V=mvM
We can also use conservation of energy to write the following equation: MgR=12mv2+12M(mvM)2
⇒mgR=12mv2(1+mM)
⇒v=
⎷2gR1+mM
Hence option (a) is correct, When point mass slides down then block moves to the left. Displacement of point mass with respect to block is R towards right. Let block moves by an amount x towards left then net displacement of point mass becomes (R - x) towards right. Since displacement of centre of mass is zero hence we can write the following:
Mx=x(R−x)
⇒x=mRM+m
We can see that option() is also correct. Negative sign is applied because it has moved towards negative side of the origin.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )
3 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
48 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Knowledge Check
A block of mass √3kg rests on a horizontal frictionless surface. What will be the acceleration of the block if it is subjected to two forces as shown in the figure.
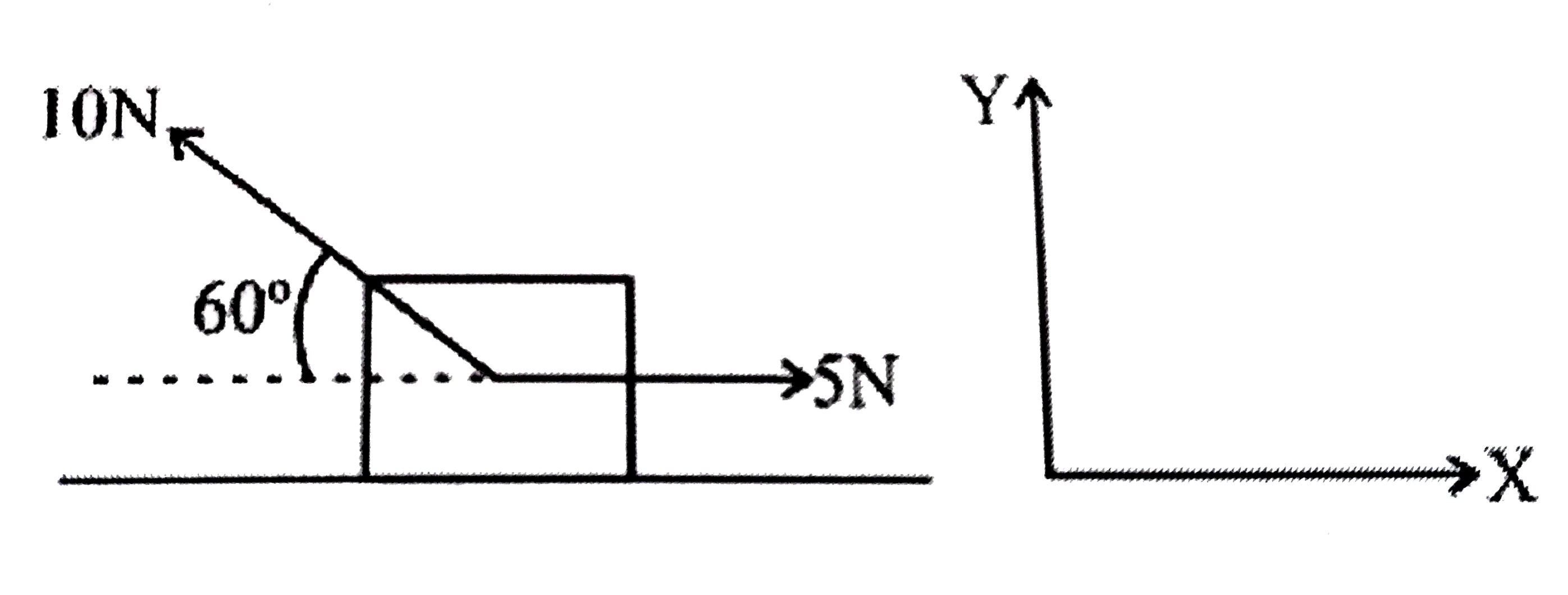 AAcceleration will be along Y-axisBAcceleration will be along X-axisCAcceleration will be in between X & YDNo acceleration will be there
AAcceleration will be along Y-axisBAcceleration will be along X-axisCAcceleration will be in between X & YDNo acceleration will be thereTwo blocks each of mass M are resting on a frictionless inclined plane as shown in fig then:
 Athe block A moves down the planeBthe block B moves down the planeCboth the blocks remain at restDboth the blocks move down the plane
Athe block A moves down the planeBthe block B moves down the planeCboth the blocks remain at restDboth the blocks move down the planeA block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is
 A2π√mK+√2LsinθgB2π√mK+√2(L−l)gsinθC2π√(L−l)gsinθ+√mKDnone of these
A2π√mK+√2LsinθgB2π√mK+√2(L−l)gsinθC2π√(L−l)gsinθ+√mKDnone of these
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA block of mass 2 m is pulled along a horizontal frictionless surface by a rope of mass m as shown in the figure given. What force is exerted by the rope on the block ?

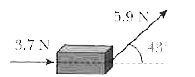
View SolutionTwo forces act on a 4.5 kg block resting on a frictionless surface as shown in the given figure. What is the magnitude of the horizontal acceleration of the block ?
View SolutionTwo blocks, each having a mass M, rest on frictionless surfaces as shown in the figure. If the pulleys are light and frictionless and M on the incline is allowed to move down, then the tension in string will be

View SolutionA block of mass m moves on a horizontal rough surface with initial velocity v. The height of the centre of mass of the block is h from the surface. Consider a point A on the surface.
View Solution