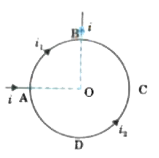
There is a circular loop of current of radius , as shown in figure: If current enters at point A and leaves at point B where ∠AOB is 90∘ and the wire of the loop is of uniform cross section area, then calculate the magnetic field intensity at the centre of the loop.
0
3μ0i16r
μ0i32r
3μ0i32r
The correct Answer is:A
Let R be the resistance of portion AB, then 3R will be the resistance of the remaining loop because AB is just a quarter of the circle. Both the parts will have the same potential difference between points A and B. For the same potential difference, using V=iR, we can understand that the current will be distributed inversely proportional to their resistances. Hence currents flowing in the two parts of the loop will be as follows:
i1=3RR+3Ri=3i4
i2=RR+3Ri=i4
Magnetic field intensity at the centre due to part AB can be written as follows:
B1=14[μ0i12r]=14⎡⎣μ03i42r⎤⎦=3μ0i32r
Magnetic field intensity due to the part BCDA can be written as follows:
B2=34[μ0i12r]=34⎡⎣μ0i42r⎤⎦=3μ0i32r
Both the fields are having the same magnitude but the two are opposite in direction and hence the net magnetic field at the centre of the loop becomes zero.
Note that we can predict the answer with just a bit of mental calculations. One portion is a quarter of the circle but current is three times than the other part which is three quarters of the circle. Hence, option (a) is correct.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)79videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)28videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Numerical Problems )18videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
Similar Questions
A circular loop of radius 9.7 cm carries a current 2.3 A. Obtain the magnitude of the magnetic field at the centre of the loop .
View SolutionA square loop of length L is made of wire of uniform cross-section carrying current l as shown in figure then magnetic field at centre of square is
View Solution
Knowledge Check
- Question 1 - Select One
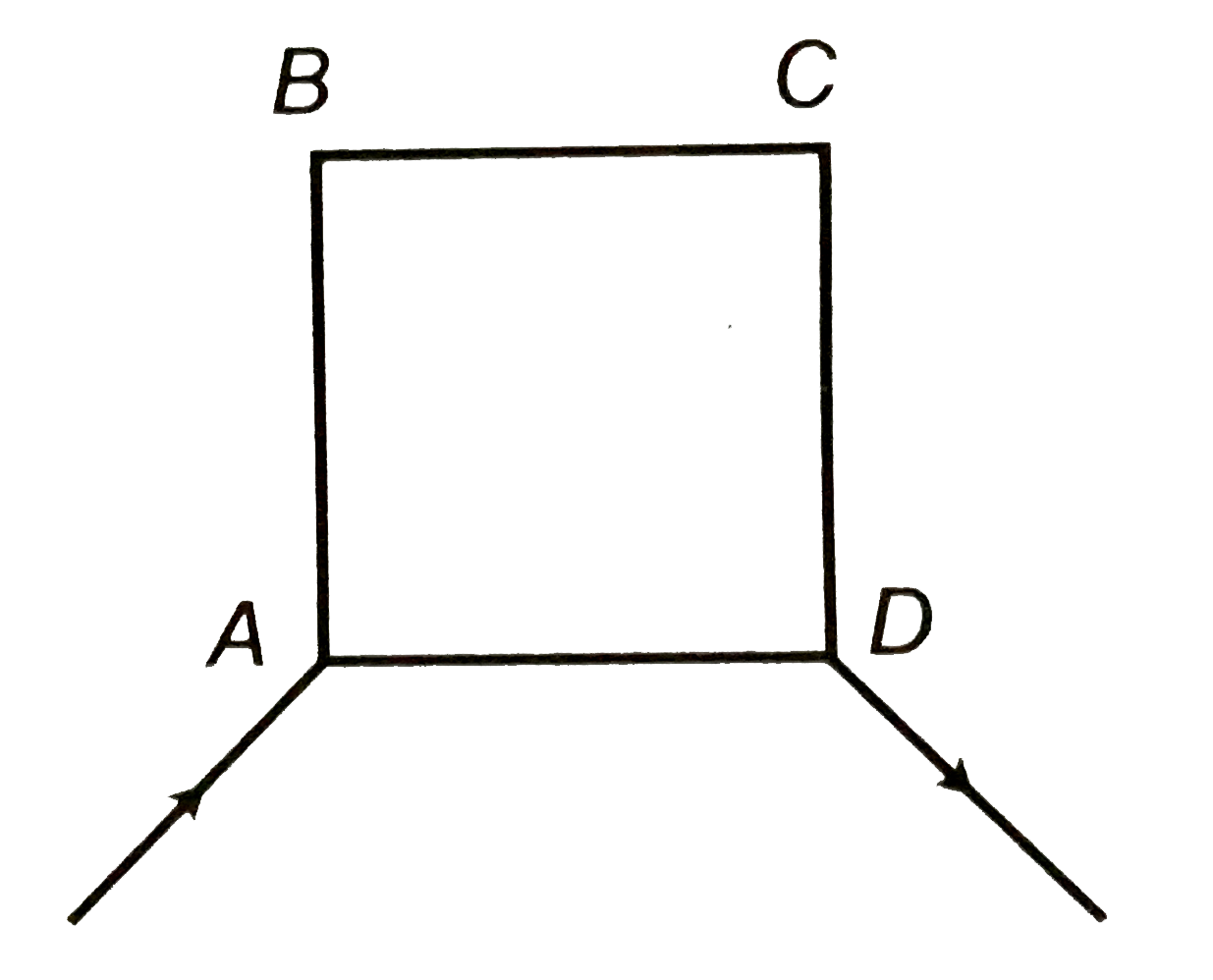
ABCD is a square loop made of a uniform conducting wire. A current enters the loop at A and leaves at D. The magnetic field is
 Azero only at the centre of the loopBmaximum at the centre of the loopCzero at all point outside the centre loopDzero at all points inside the loop
Azero only at the centre of the loopBmaximum at the centre of the loopCzero at all point outside the centre loopDzero at all points inside the loop - Question 2 - Select One
A circular loop of radius 0.0157 m carriesa current of 2.0 A. The magnetic field at the centre of the loop is
A1.57×10−5Wb/m2B8.0×10−6Wb/m2C2.5×10−5Wb/m2D3.14×10−5Wb/m2 - Question 3 - Select One
The magnetic field at the centre of a current carrying circular loop is B. If the radius of the loop is doubled, keeping the current same, the magnetic field at the centre of the loop would be :
AB4BB2C2 BD4 B
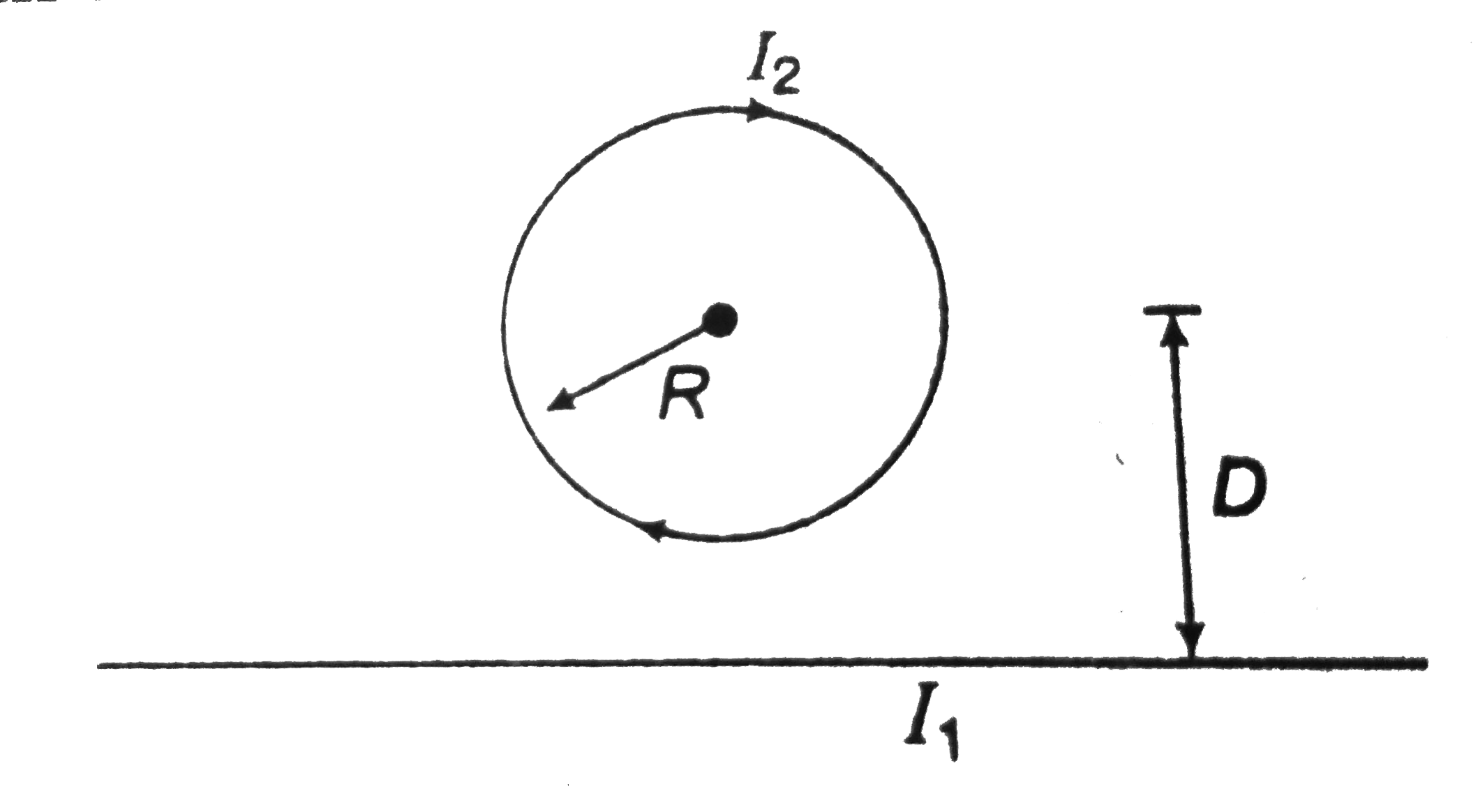
A circular loop of radius R carries current I2 in a clockwise direction as shown in figure. The centre of the loop is a distance D above a long, straight wire. What are the magnitude and direction of the current I1 in the wire if the magnetic field at the centre of loop is zero?
 View Solution
View SolutionA circular loop of radius R carries current I2 in a clockwise direction as shown in figure. The centre of the loop is a distance D above a long, straight wire. What are the magnitude and direction of the current I1 in the wire if the magnetic field at the centre of loop is zero?
 View Solution
View SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View SolutionThe magnetic field at the centre of a current carrying circular loop is B. If the radius of the loop is doubled, keeping the current same, the magnetic field at the centre of the loop would be :
View SolutionThere is one circular loop of wire of radius R, carrying current I and magnetic field at its centre is B0, due to its own current. The loop is bent along its diameter at right angle. What will be the net magnetic field at the centre of the loop?
View Solution

