Question

This displacement time graph of a particle executing S.H.M. is given in figure : (sketch is schematic and not to scale).

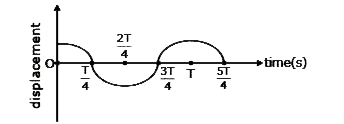
Which of the following statements is/are true for this motion?
(A) The force is zero at t = $\frac{3T}{4}$
(B)The acceleration is maximum at t=T
(C )The speed is maximum at t = $\frac{T}{4}$
(D) The P.E. is equal to K.E. of the oscillation at t = $\frac{T}{2}$

Options

A. (B), (C ) and (D)
B. (A) ,(B) and (D)
C. (A) and (D )
D. (A),(B) and (C )

Answer

A::B::C

Explanation

at `t = (3T)/4`
Particle is at mean position
a = 0
F = 0
(B) at t= T,
Particle is at extreme.
F is maximum
a = max
(C) at `t =T/4` , mean position
so, maximum velocity
(d) KE = PE
`1/2 k (A^(2) - x^(2)) = 1/2 kx^(2)`
`A^(2) - x^(2) = x^(2)`
`A^(2) = 2x^(2)`
`A = sqrt(2)x`
`x = A/(sqrt(2))` A cos `omega ` t
`x = A/(sqrt(2))` = A cos `omega `t
cos `omega t = 1/(sqrt(2))`
`omega t = pi/4`
`(2pi)/T . t = x/4 rArr t = T/8 `