Three bodies of masses m, 2m and 3m are placed at the corners of a triangle having coordinates (1, 1.5), (2.5, 1.5) and (3, 3) respectively. Calculate the coordinates of the centre of mass.
The correct Answer is:(156,94)
To find the coordinates of the center of mass of the three bodies with masses m, 2m, and 3m located at the points (1,1.5), (2.5,1.5), and (3,3) respectively, we can use the formula for the center of mass:
Center of Mass (CM)=∑mi⋅ri∑mi
where mi is the mass of each body and ri is the position vector of each body.
Step 1: Identify the masses and their coordinates
- Mass m1=m at coordinates (x1,y1)=(1,1.5)
- Mass m2=2m at coordinates (x2,y2)=(2.5,1.5)
- Mass m3=3m at coordinates (x3,y3)=(3,3)
Step 2: Calculate the total mass
Total mass=m1+m2+m3=m+2m+3m=6m
Step 3: Calculate the x-coordinate of the center of mass
Using the formula for the x-coordinate of the center of mass:
xCM=m1x1+m2x2+m3x3m1+m2+m3
Substituting the values:
xCM=m⋅1+2m⋅2.5+3m⋅36m
=m+5m+9m6m=15m6m=156=2.5
Step 4: Calculate the y-coordinate of the center of mass
Using the formula for the y-coordinate of the center of mass:
yCM=m1y1+m2y2+m3y3m1+m2+m3
Substituting the values:
yCM=m⋅1.5+2m⋅1.5+3m⋅36m
=1.5m+3m+9m6m=13.5m6m=13.56=2.25
Step 5: Combine the results
The coordinates of the center of mass are:
CM=(xCM,yCM)=(2.5,2.25)
Final Answer
The coordinates of the center of mass are (2.5,2.25).
---
- Mass m1=m at coordinates (x1,y1)=(1,1.5)
- Mass m2=2m at coordinates (x2,y2)=(2.5,1.5)
- Mass m3=3m at coordinates (x3,y3)=(3,3)
Total mass=m1+m2+m3=m+2m+3m=6m
Using the formula for the x-coordinate of the center of mass:
xCM=m1x1+m2x2+m3x3m1+m2+m3
Substituting the values:
xCM=m⋅1+2m⋅2.5+3m⋅36m
=m+5m+9m6m=15m6m=156=2.5
Using the formula for the y-coordinate of the center of mass:
yCM=m1y1+m2y2+m3y3m1+m2+m3
Substituting the values:
yCM=m⋅1.5+2m⋅1.5+3m⋅36m
=1.5m+3m+9m6m=13.5m6m=13.56=2.25
The coordinates of the center of mass are:
CM=(xCM,yCM)=(2.5,2.25)
The coordinates of the center of mass are (2.5,2.25).
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Conceptual Questions
24 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS TOUGH & TRICKY
8 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Chapter Practice Test (for Board Examination)
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Three blocks of uniform thickness and masses m,mand2m are placed at the corners of a triangle having co-ordinates (2.5,1.5),(3.5,1.5)and(3,3) respectively. Find the co-ordinates of the centre of mass of the system.
View SolutionThree point masses of 1kg, 2kg and 3kg lie at (0,0), (1,2), (3,−1) respectively. Calculate the coordinates of the centre of mass of the system.
View Solution
Knowledge Check
A system consists of 3 particles each of mass m located at points (1, 1), (2, 2) and (3, 3). The coordinates of the centre of mass are
A(6,6)B(3,3)C(1 ,1)D(2 ,2)
Two bodies of masses 1 kg and 2 kg are located at (1,2) and (-1,3), respectively. Calculate the coordinates of center of mass.
View SolutionTwo bodies of masses 1 kg and 3 kg are lying in xy plane at (0, 0) and (2, -1) respectively. What are the coordinates of the centre of mass ?
View SolutionThree particles of masses m,m and 4kg are kept at a verticals of triangle ABC. Coordinates of A, B and C are (1,2) , (3,2) and (−2,−2) respectively such that the centre of mass lies at origin. Find the value of mass m.
Hint. xcm=∑3i−1mixi∑3i=1mi, ycm=∑3i=1miyi∑3i=1mi
View SolutionThree particles of the same mass lie in the x-y plane. The (x,y) coordinates of their positions are (1,1),(2,2) and (3,3) respectively. The (x-y) coordinates of the centre of mass are:
View SolutionThree particles having their masses in the ratio 1:3:5 are kept at the vertices of a triangle ABC. Coordinate of A, B and C are (9,−3), (3,4) and (0,0). Find the coordinates of the centre of mass.
Hint. xcm=∑3i−1mixi∑3i=1mi, ycm=∑3i=1miyi∑3i=1mi
View SolutionThree particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
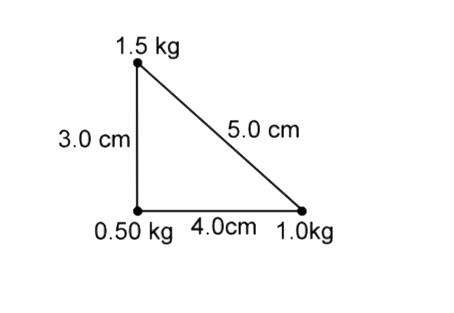
View SolutionThree particles of masses 0.5 kg, 1.0 kg and 1.5 kg are placed at the three corners of a right angled triangle of sides 3.0 cm, 4.0 cm and 5.0 cm as shown in figure. Locate the centre of mass of the system.
View Solution
