Three capacitors of capacitances 3μF,9μF and 18μF are connected one in series and another time in parallel. The ratio of equivalent capacitance in the two cases (CsCp) will be
1:15
15:1
1:1
1:3
The correct Answer is:A
Step by step video & image solution for Three capacitors of capacitances 3 muF, 9muF and 18 muF are connected one in series and another time in parallel. The ratio of equivalent capacitance in the two cases ((C_(s))/(C_(p))) will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises17videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.520videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery37videos
ELECTROSTATICS
Similar Questions
Three capacitors of capacitances 1μF,2μFand4μF are connected first in a series combination, and then in parallel combination. The ratio of their equivalent capacitances will be
View SolutionTwo identical capacitors are first connected in series and then in parallel. The ratio of equivalent capacitance is
View SolutionThree capacitors of capacitance 3μF are connected in a circuit. Then, their maximum and minimum capacitance will be
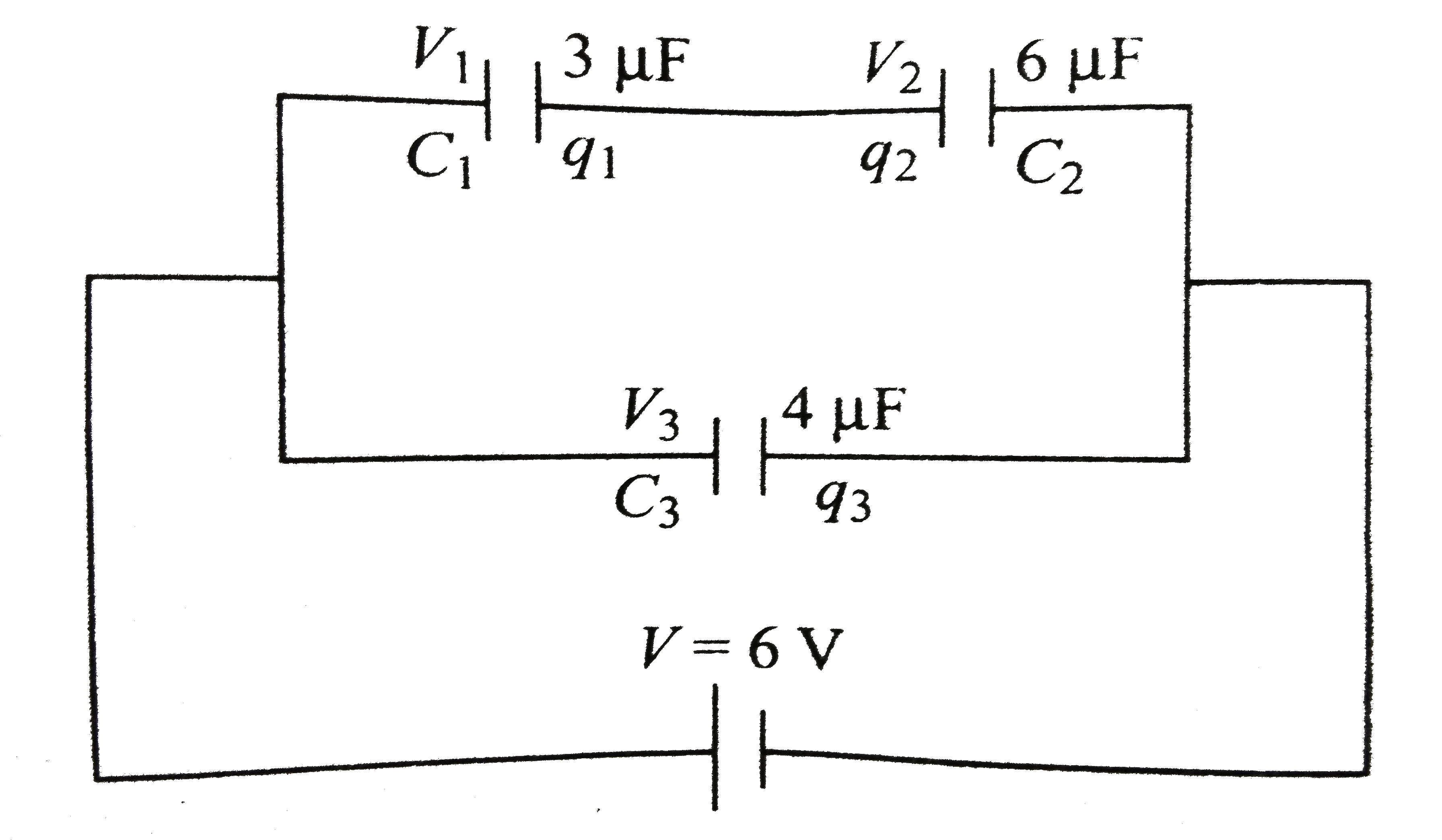
View SolutionThree capacitors of capacitances 3μF, 6μF, and 4μF are connected as shown across a battery of emf 6V.
.
i. Find the equivalent capacitance,
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in the system of capacitors and total energy stored in the system of capacitor.View SolutionFour capacitors of each of capacity 3μF are connected as shown in the adjoining figure. The ratio of equivalent capacitance between A and B and between A and C will be
View SolutionTwo capacitors of capacitance of 6μFand12μF are connected in series with a battery. The voltage across the 6μF capacitor is 2V. Compute the total battery voltage.
View SolutionTwo capacitor of capacitance 4.0μFand 6.0muF' are connected in series with a battery of 20 V . Find the energy supplied by the battery .
View SolutionThree capcitors of capacitances 4μF,
.
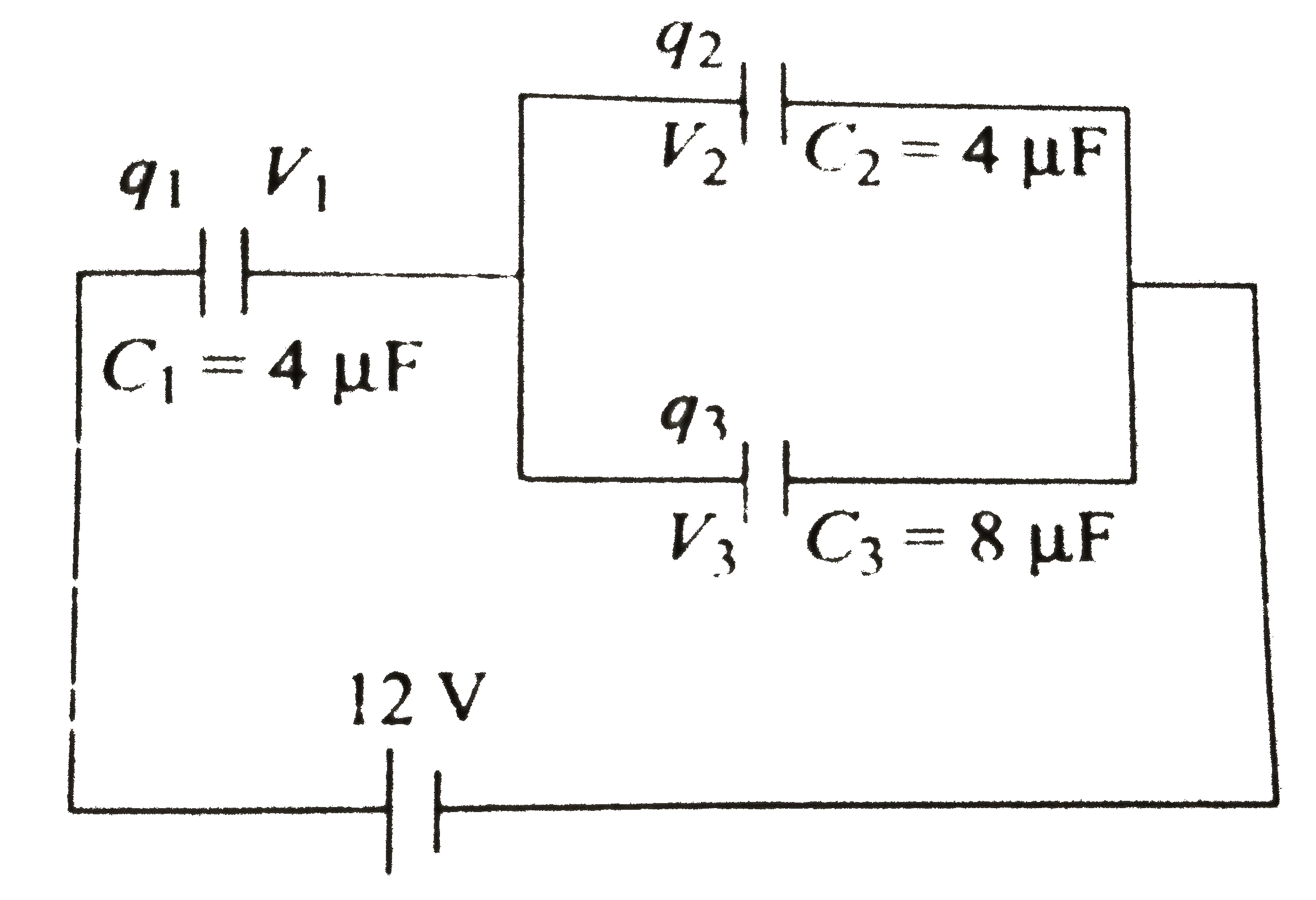4μF, and 8μF, are connected as show across a battery of emf 12V.
i. Find the equivalent capacitane.
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in each capacitor and the total energy stored in the system of capacitors.View SolutionThree capacitors having capacitances of 8.4μF,8.4μF and 4.2μF are connected in series across a 36 potential difference.
(a) What is the charge on 4.2μF capacitor?
(b) What is the total energy stored in all three capacitors?
(c) The capacitors are disconnected from the potential difference without allowing them to discharge. They are then reconnected in parallel with each other, with the positively charged plates connected together. What is the voltage across each capacitor in the parallel combination?
(d) What is the total energy now stored in the capacitors?View SolutionThree capacitors each of capacitance C are connected in series. Their equivalent capacitance is Cs. The same three capacitors are now connected in parallel. Their equivalent capacitance becomes Cp. Find the ratio (CpCs)
(Working must be shown).View Solution