Three conducting spheres A, B and C are shown in figure. The radii of the spheres are a, b and c respectively. A and B connected by a conducting wire. The capacity of the system is
The correct Answer is:B
To find the capacitance of the system consisting of three conducting spheres A, B, and C, where A and B are connected by a conducting wire, we can follow these steps:
1. Understanding the Configuration:
- We have three conducting spheres: A (radius = a), B (radius = b), and C (radius = c).
- Spheres A and B are connected by a conducting wire, which means they will share the same electric potential.
2. Charge Distribution:
- When A and B are connected, any excess charge will redistribute between them until they reach the same potential. Since sphere A has no charge on its surface when connected to B, we can ignore it in our calculations for capacitance.
3. Effective Capacitance:
- The capacitance of two spheres can be calculated using the formula for capacitance between two spheres:
C=4πϵ0b⋅cc−b
- Here, ϵ0 is the permittivity of free space, b is the radius of sphere B, and c is the radius of sphere C.
4. Final Expression:
- Thus, the capacitance of the system formed by spheres B and C is:
C=4πϵ0b⋅cc−b
5. Conclusion:
- Therefore, the capacitance of the system is given by the expression above.
- We have three conducting spheres: A (radius = a), B (radius = b), and C (radius = c).
- Spheres A and B are connected by a conducting wire, which means they will share the same electric potential.
- When A and B are connected, any excess charge will redistribute between them until they reach the same potential. Since sphere A has no charge on its surface when connected to B, we can ignore it in our calculations for capacitance.
- The capacitance of two spheres can be calculated using the formula for capacitance between two spheres:
C=4πϵ0b⋅cc−b
- Here, ϵ0 is the permittivity of free space, b is the radius of sphere B, and c is the radius of sphere C.
- Thus, the capacitance of the system formed by spheres B and C is:
C=4πϵ0b⋅cc−b
- Therefore, the capacitance of the system is given by the expression above.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Matrix Matching
2 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
Knowledge Check
Two spheres of radius a and b respectively are charged and joined by a wire. The ratio of electric field of the spheres is
AabBbaCa2b2Db2a2
(Figure 3.114) shows three concentric spherical conductors A,B,andC with radii R,2R, and 4R, respectively. A and C are connected by a conducting wire, and B is uniformly charged (charge=+Q). Find
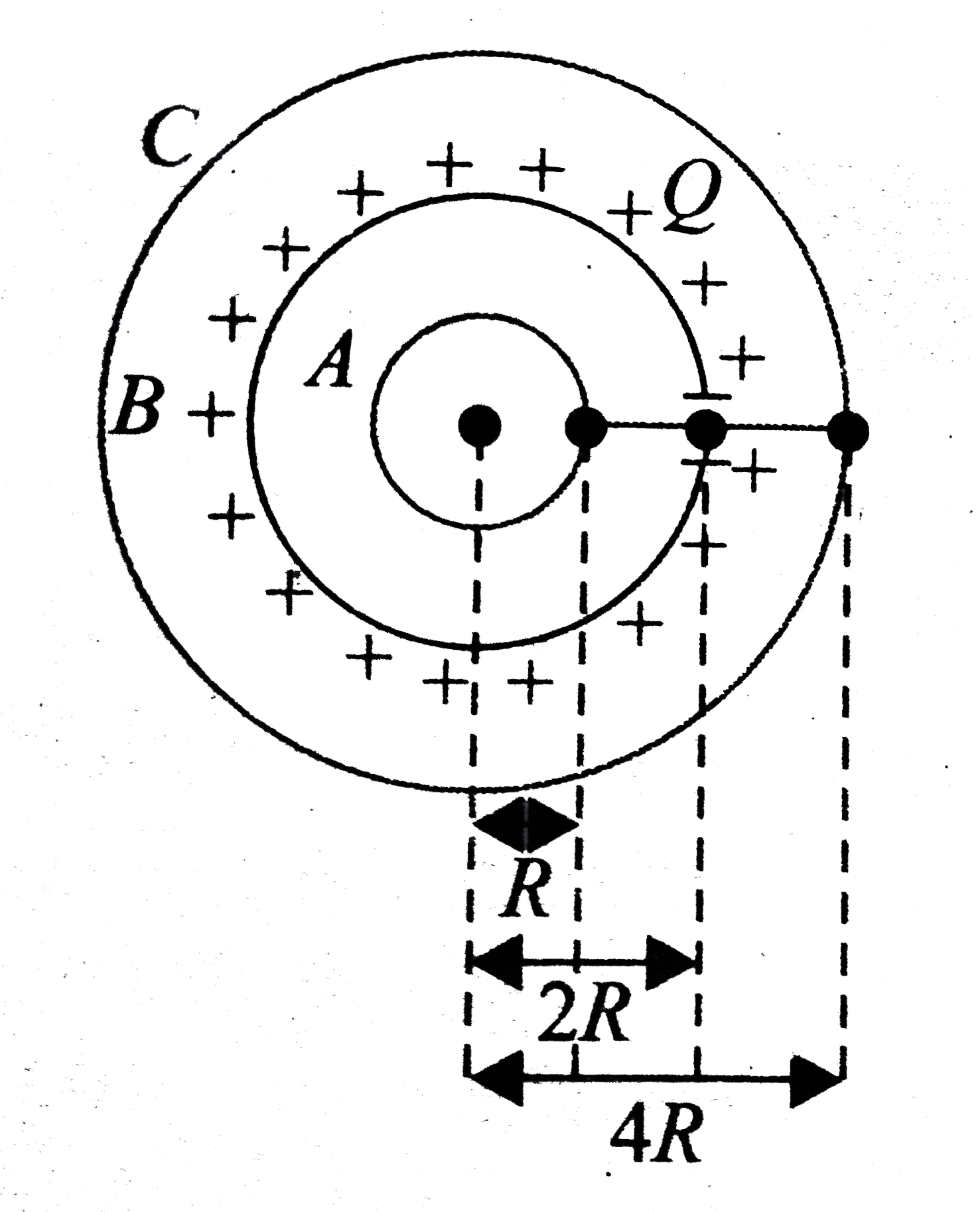 .
.
a. charges on conductors A and C, and
b. potentials of A and B.
View SolutionTwo concentric hollow conducting spheres of radius a and b (b>a) contains charges Qa and Qb respectively. If they are connected by a conducting wire then find out following
(i) Final charges on inner and outer spheres.
(ii) Heat produced during the process.
View SolutionThree long straight wires A, B and C are carrying current as shown in figure. Then the resultant force on B is directed

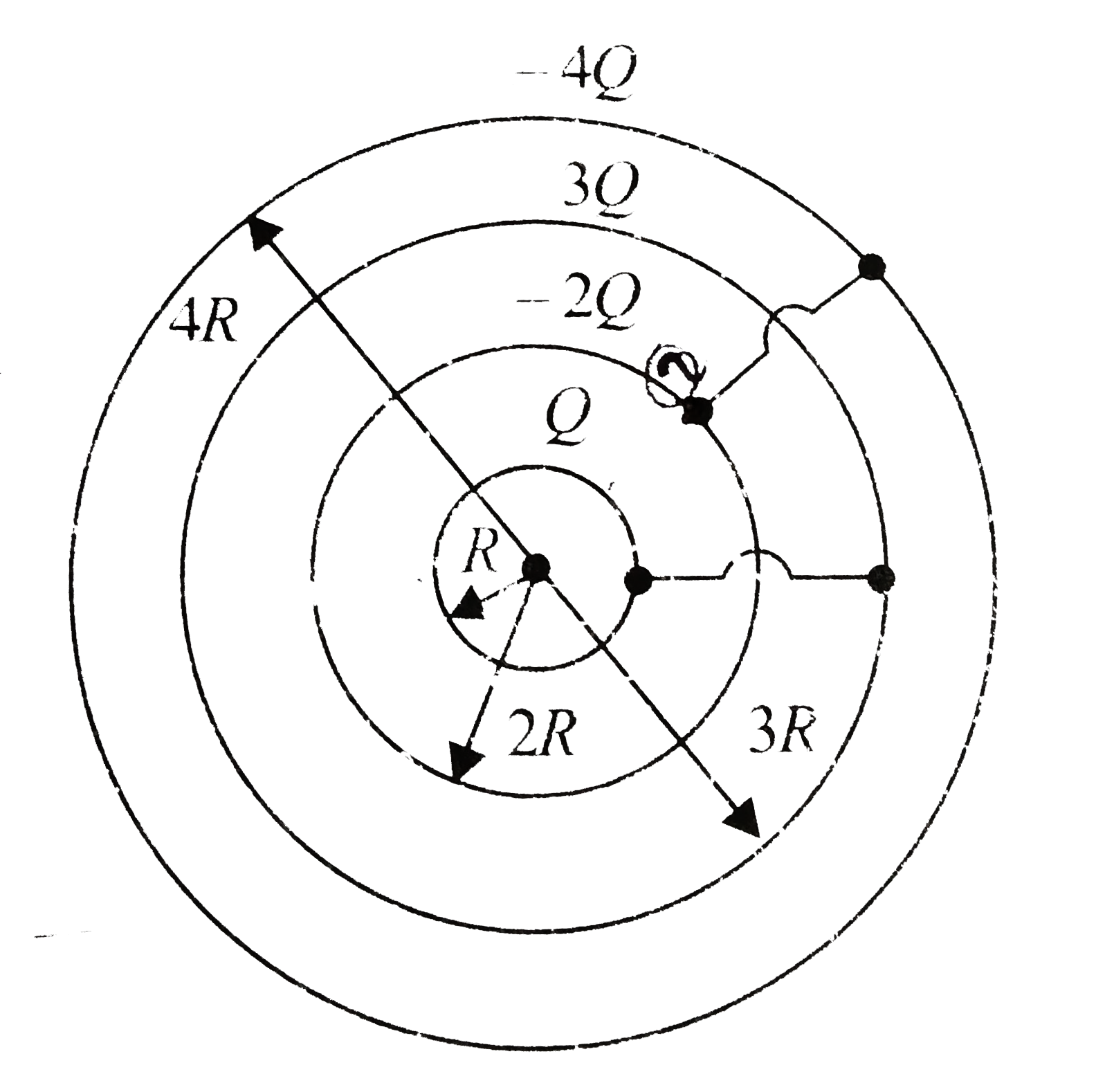
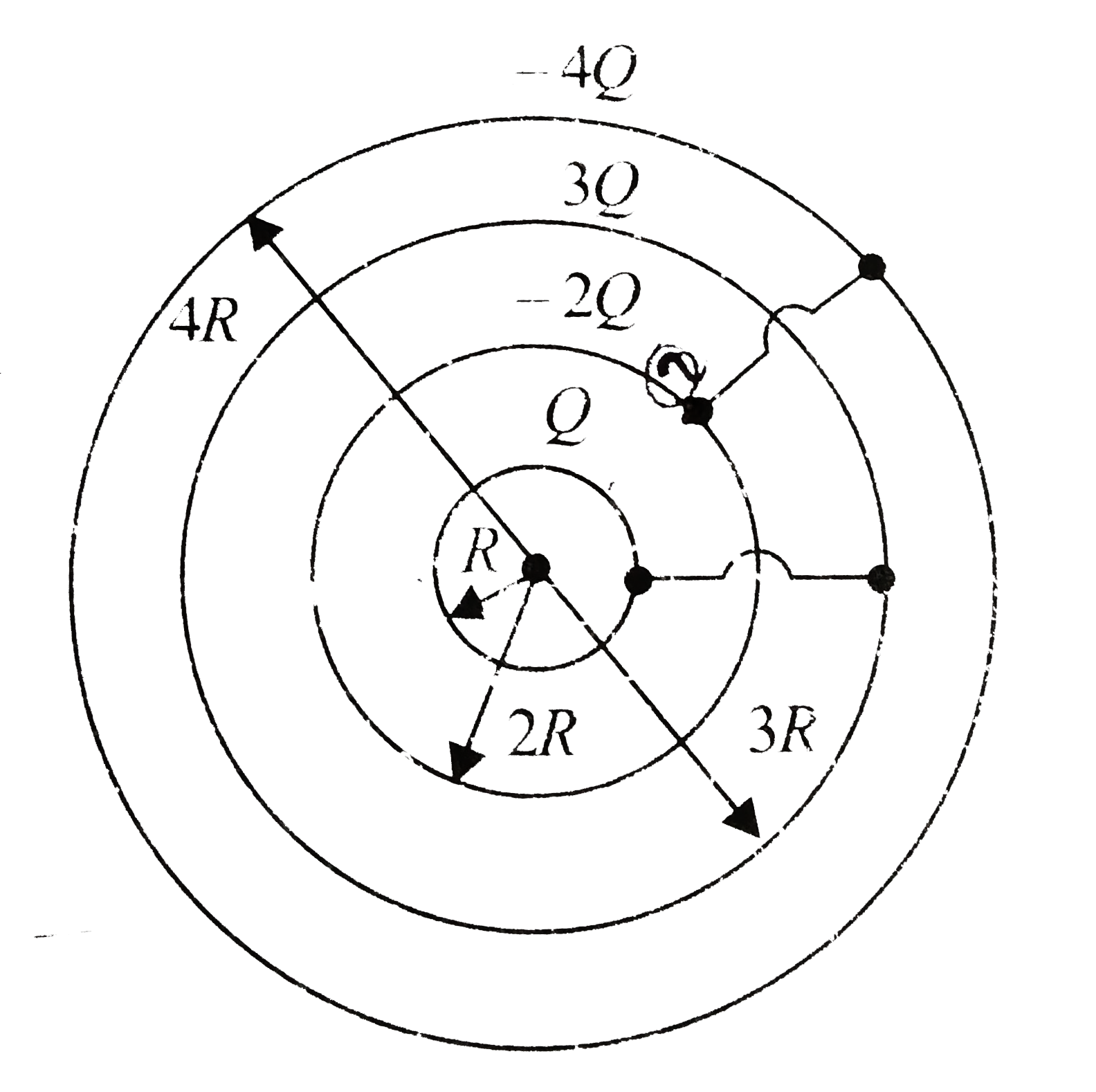
View SolutionFour concentric hollow spheres of radii R, 2R, 3R, and 4R are given the charges as shown in figure. Then the conductors 1 and 3, 2 and 4 are connected by conducting wires (both the connections are made at the same time.) .find thr potential of last sphere
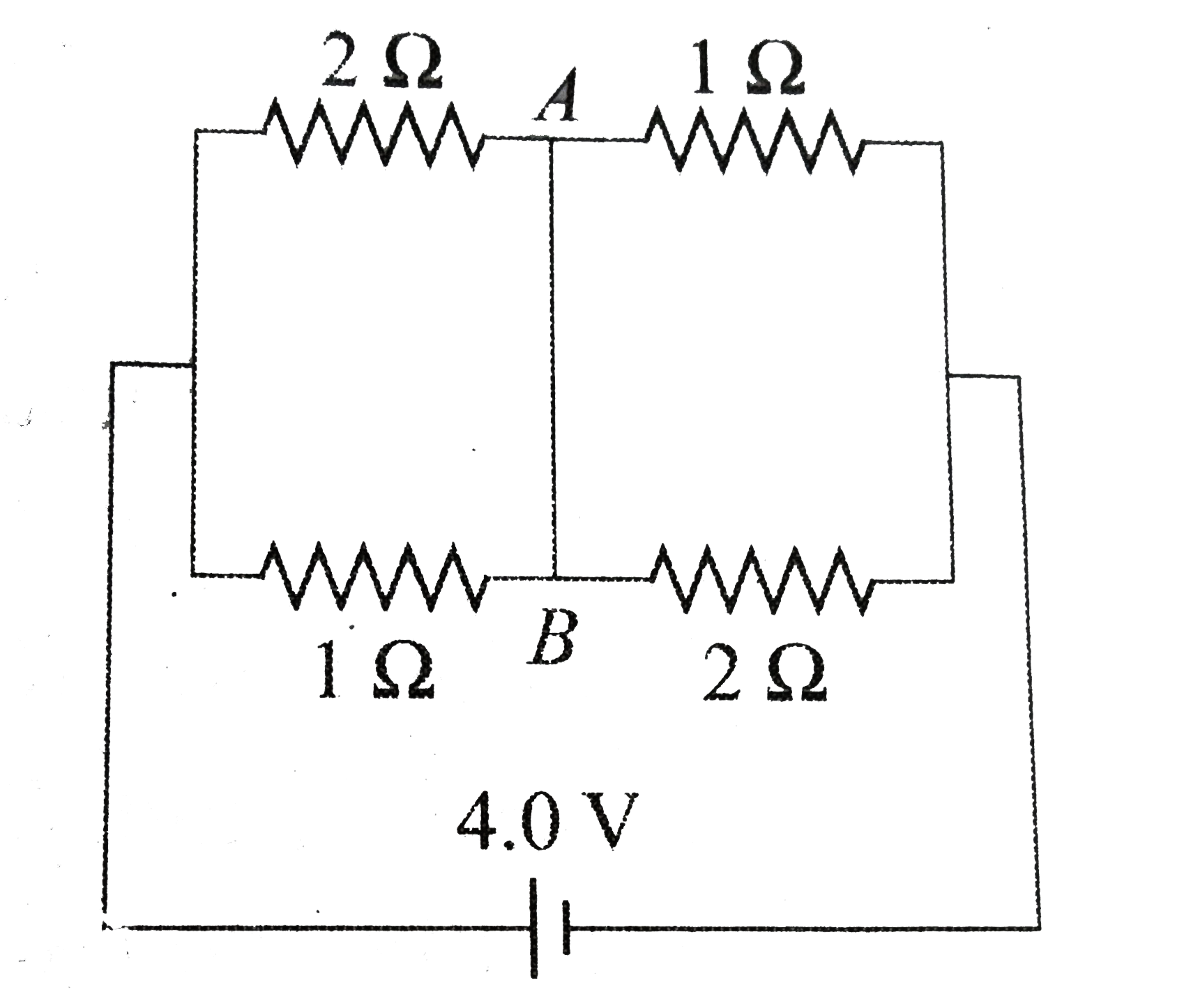
View SolutionIn Figure points A and B are connected by a perfectly conducting wire. Calculate the current through AB
View SolutionFour concentric hollow spheres of radii R, 2R, 3R, and 4R are given the charges as shown in figure. Then the conductors 1 and 3, 2 and 4 are connected by conducting wires (both the connections are made at the same time.)
 ,
,
The charge on the inner surface of the third conductor is
View SolutionFour concentric hollow spheres of radii R, 2R, 3R, and 4R are given the charges as shown in figure. Then the conductors 1 and 3, 2 and 4 are connected by conducting wires (both the connections are made at the same time.)
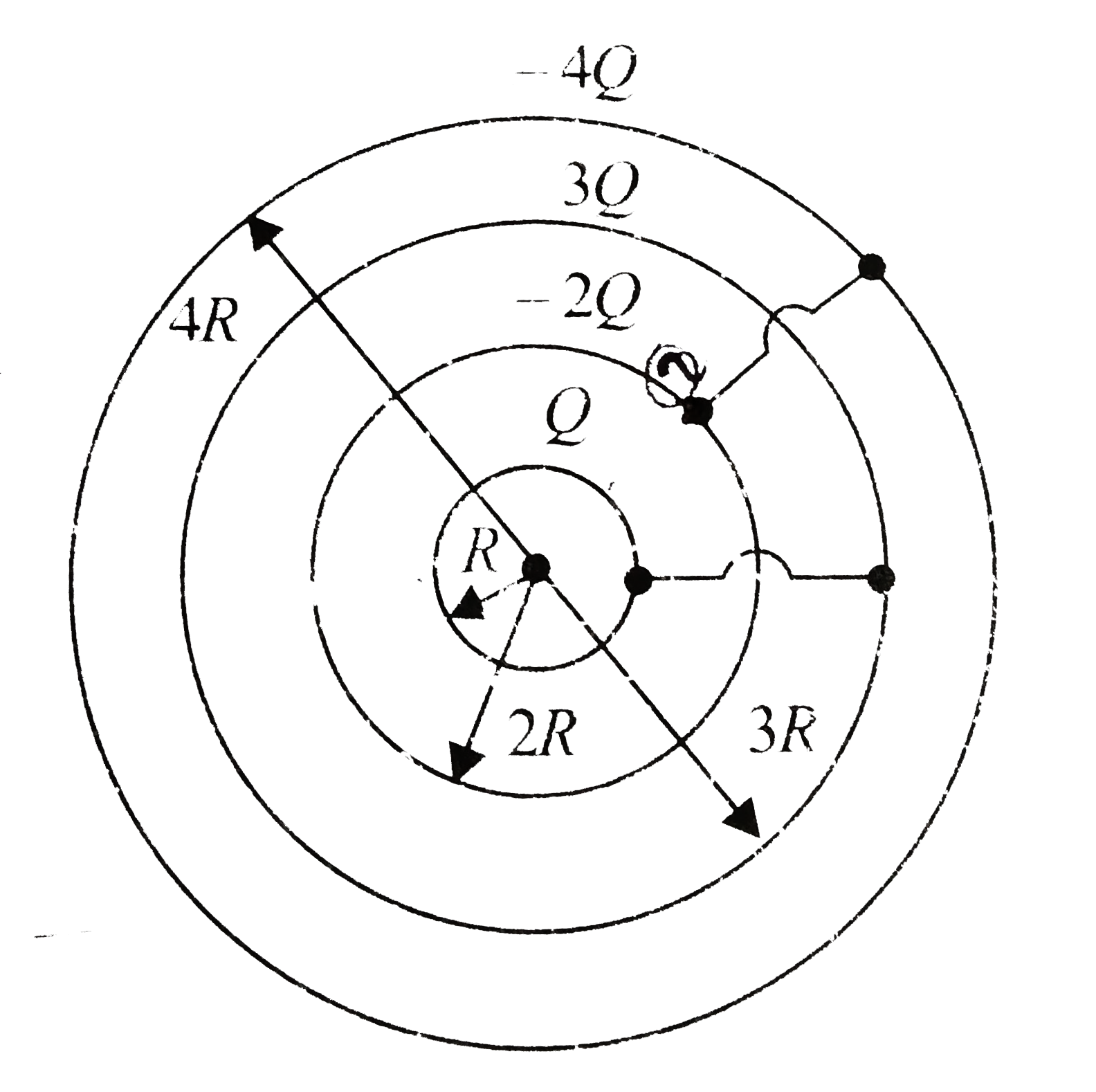
View Solution

_S01_014_Q01.png) .
.