Two concentric spherical conducting shells of radii R and 2R are carrying charges q and 2q, respectively. Both are now connected by a conducting wire. Find the change in electric potential (inV) on the outer shell.
zero
3kQ2R
kQR
2kQR
The correct Answer is:A
To solve the problem step by step, we will analyze the situation involving two concentric spherical conducting shells with given charges and radii.
Step 1: Understand the Initial Setup
We have two concentric spherical conducting shells:
- Inner shell radius = R, charge = q
- Outer shell radius = 2R, charge = 2q
Step 2: Calculate the Initial Potential on the Outer Shell
The electric potential V at a point outside a charged spherical shell is given by the formula:
V=kQr
where k is Coulomb's constant, Q is the charge, and r is the distance from the center.
1. Potential due to the inner shell (charge q) at the surface of the outer shell (radius 2R):
Vinner=kq2R
2. Potential due to the outer shell (charge 2q) at its own surface (radius 2R):
Vouter=k2q2R=kqR
3. Total initial potential on the outer shell:
Vinitial=Vinner+Vouter=kq2R+kqR=kq2R+k2q2R=k3q2R
Step 3: Connect the Shells with a Conducting Wire
When the two shells are connected by a conducting wire, charge will redistribute until both shells reach the same potential.
Let x be the charge on the inner shell after connecting, then the charge on the outer shell will be 3q−x (since total charge is conserved).
Step 4: Set Up the Equation for Final Potential
The final potential on both shells must be equal:
1. Potential on the inner shell after redistribution:
Vinner=kxR+k3q−x2R
Simplifying:
Vinner=k(xR+3q−x2R)=k(2x+3q−x2R)=kq+x2R
2. Potential on the outer shell after redistribution:
Vouter=k3q−x2R
Setting these two potentials equal:
kq+x2R=k3q−x2R
Step 5: Solve for x
Cancelling k/2R from both sides:
q+x=3q−x
2x=2q⟹x=q
Step 6: Determine Final Charge Distribution
- Charge on the inner shell after connection = x=q
- Charge on the outer shell after connection = 3q−x=3q−q=2q
Step 7: Calculate the Final Potential on the Outer Shell
The final potential on the outer shell:
Vfinal=k2q2R+kqR=kqR+kqR=k2qR
Step 8: Calculate the Change in Electric Potential
The change in electric potential on the outer shell is:
ΔV=Vfinal−Vinitial=k2qR−k3q2R
Finding a common denominator:
ΔV=k(4q2R−3q2R)=kq2R
Final Answer
The change in electric potential on the outer shell is:
ΔV=kq2R
We have two concentric spherical conducting shells:
- Inner shell radius = R, charge = q
- Outer shell radius = 2R, charge = 2q
The electric potential V at a point outside a charged spherical shell is given by the formula:
V=kQr
where k is Coulomb's constant, Q is the charge, and r is the distance from the center.
Vinner=kq2R
Vouter=k2q2R=kqR
Vinitial=Vinner+Vouter=kq2R+kqR=kq2R+k2q2R=k3q2R
When the two shells are connected by a conducting wire, charge will redistribute until both shells reach the same potential.
The final potential on both shells must be equal:
1. Potential on the inner shell after redistribution:
Vinner=kxR+k3q−x2R
Simplifying:
Vinner=k(xR+3q−x2R)=k(2x+3q−x2R)=kq+x2R
Vouter=k3q−x2R
kq+x2R=k3q−x2R
Cancelling k/2R from both sides:
q+x=3q−x
2x=2q⟹x=q
- Charge on the inner shell after connection = x=q
- Charge on the outer shell after connection = 3q−x=3q−q=2q
The final potential on the outer shell:
Vfinal=k2q2R+kqR=kqR+kqR=k2qR
The change in electric potential on the outer shell is:
ΔV=Vfinal−Vinitial=k2qR−k3q2R
Finding a common denominator:
ΔV=k(4q2R−3q2R)=kq2R
The change in electric potential on the outer shell is:
ΔV=kq2R
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Matrix Matching
2 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
Two concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionTwo concentric spherical conducting shells of radii r and R (r<R) carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
View SolutionTwo concentric spherical conducting shells of radii R and 2R carry charges Q and 2Qrespectively.Change in electric potential on the outer shell when both are connected by a conducting wire is (k=14πɛ0)
View SolutionThree concentric conducting spherical shells of radii R, R2 and 3R carry charges Q,-2Q and 3Q, respectively compute the electric field at r=52R

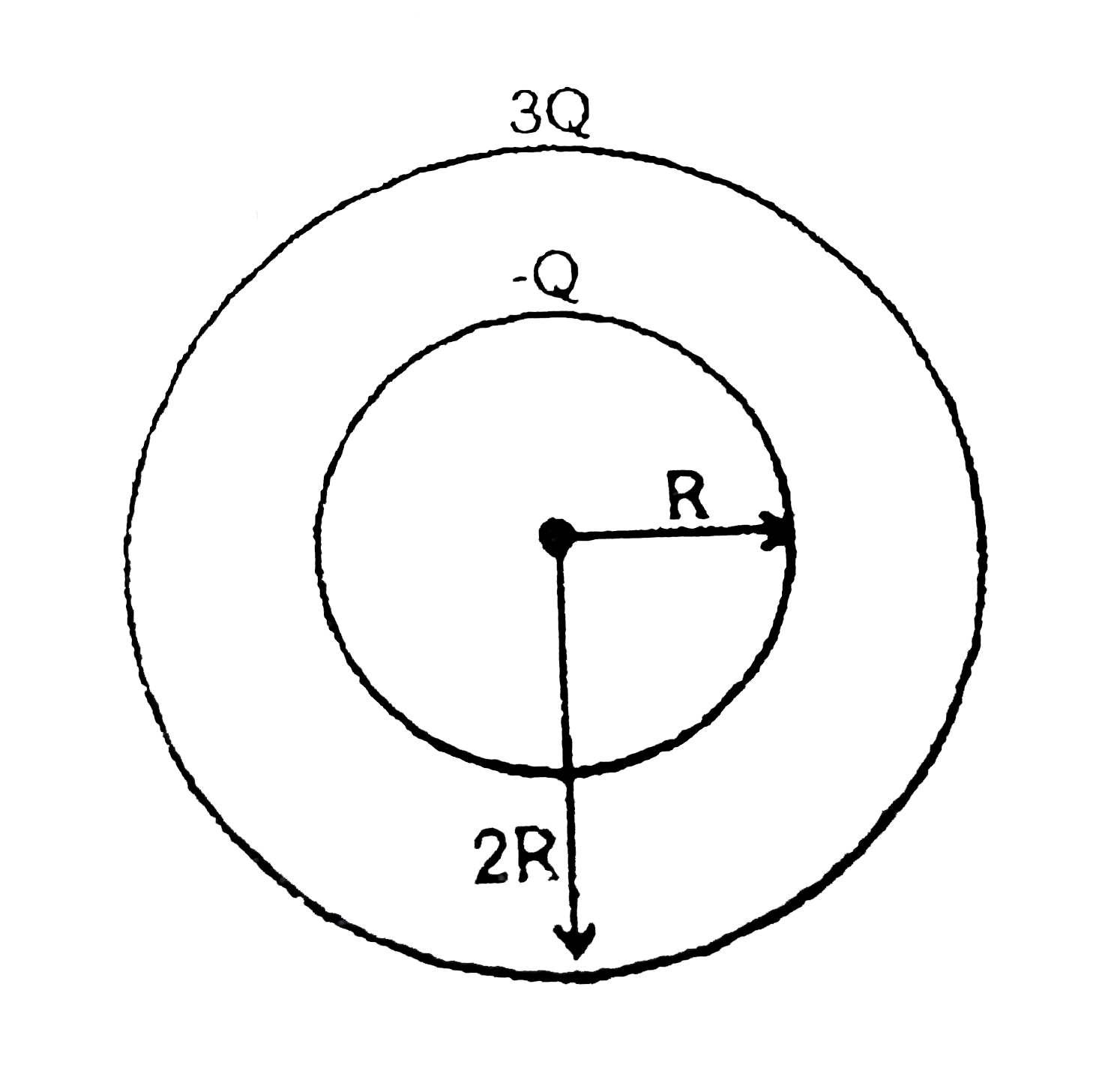
View SolutionTwo conducting hollow spherical shells of radius R and 2R carry charges -Q and 3Q respectively. How much charge will flow into the earth if inner shell is grounded?
View SolutionConsider two concentric metalic shell's of radii R and 2R. The inner shell is having charge Q and outer shell is uncharged. If they are connected with a conducting wire. Then,
View SolutionTwo concentric conducting thin shells of radius R and 2 R carry charges +Q and +3Q respectively. The magnitude of electric field at a distance x outside and inside from the surface of outer sphere is same. Then the value of x is

View SolutionTwo uniformly charged concentric spherical shells of radius R and r, are given charges Q1 and Q2 respectively. If their potential difference is V, then it will not depends upon:

View SolutionTwo concentric conducting spherical shells of radii a1anda2(a2>a1) are charged to potentials ϕ1 and ϕ2, respectively. Find the charge on the inner shell.
View SolutionThree concentric conducting spherical shells of radii R,2R and 3R carry charges Q,−2Q and 3Q, respectively.
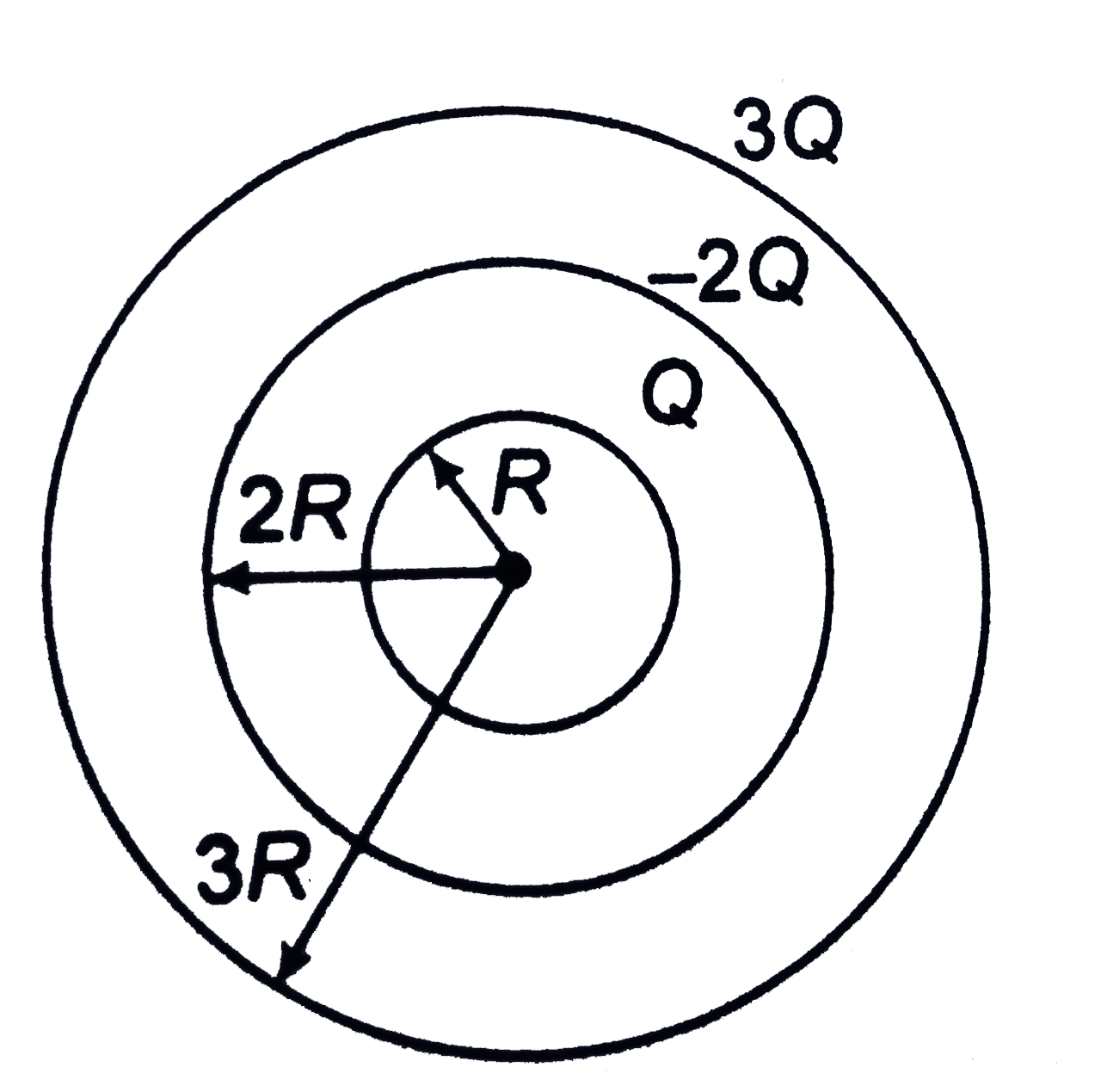
a. Find the electric potential at r=R and r=3R where r is the radial distance from the centre . b. Compute the electric field at r=52R
c. Compute the total electrostatic energy stored in the system.
The inner shell is now connected to the external one by a conducting wire, passing through a very small hole in the middle shell.
d. Compute the charges on the spheres of radii R and 3R.
e. Compute the electric field at r=52R
View Solution
