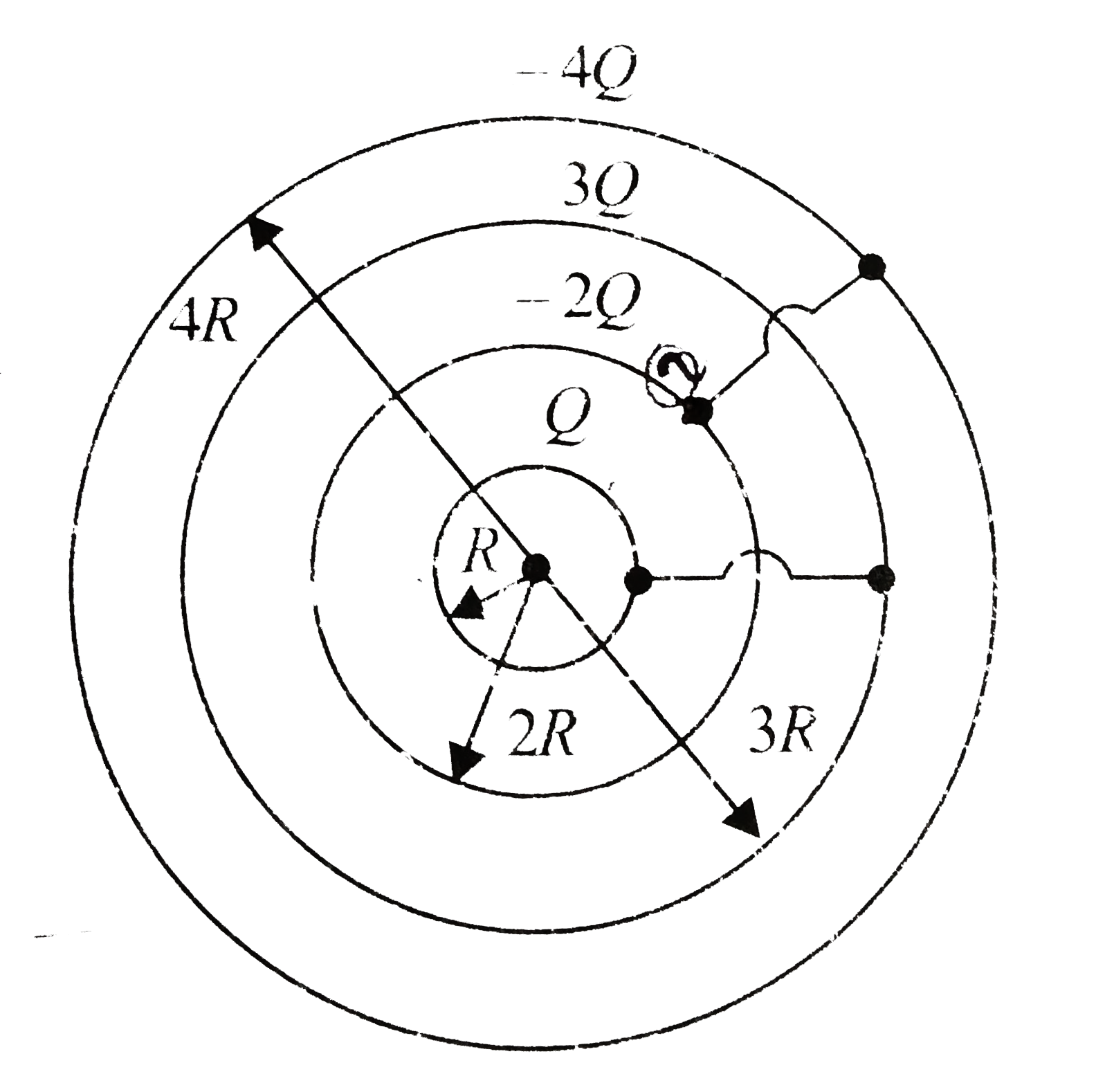
Four concentric hollow spheres of radii R, 2R, 3R, and 4R are given the charges as shown in figure. Then the conductors 1 and 3, 2 and 4 are connected by conducting wires (both the connections are made at the same time.) .find thr potential of last sphere
−Q/8πε0R
Q/8πε0R
Q/32πε0R
−Q/32πε0R
The correct Answer is:B

Let the charge distribution be as shown in fig
From gauss's theorem we know that facing surface s of the conductor acquire equal and oppsite charges. So
V1=V3 and V2=V4
q1+q3−q2=+4Q .(i)
Now, q2−q1+q4−q3=−6Q ..(ii)
V1=14πε0[q1R+q2−q12R+q3−q23R+q4−q34R]
V2=14πε0[q12R+q2−q12R+q3−q23R+q4−q34R]
V3=14πε0[q13R+q2−q13R+q3−q23R+q4−q34R]
V4=14πε0[q14R+q2−q14R+q3−q23R+q4−q34R]
from V1=V3,q1=−q23
from V2=V4,q2=−q32
On solving eq. (ii) q1=2Q5,q2=−6Q5 and q3=12Q5
Substituting these values in Eq (ii) we get q4=−2Q
charge on the inner surface of the third conductor is −q2=6Q/5
charge on the fouth conductor is q4−q3=−2Q−12Q5=−22Q5
potential of conduction 1, V1=−3Q40πε0R=V3
Potential of conductor 2, V2=Q8πε0R=V4
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Interger Answer type
20 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Fill in the blanks
10 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Four concentric hollow spheres of radii R, 2R, 3R, and 4R are given the charges as shown in figure. Then the conductors 1 and 3, 2 and 4 are connected by conducting wires (both the connections are made at the same time.). The final charge on conductor 4 is-
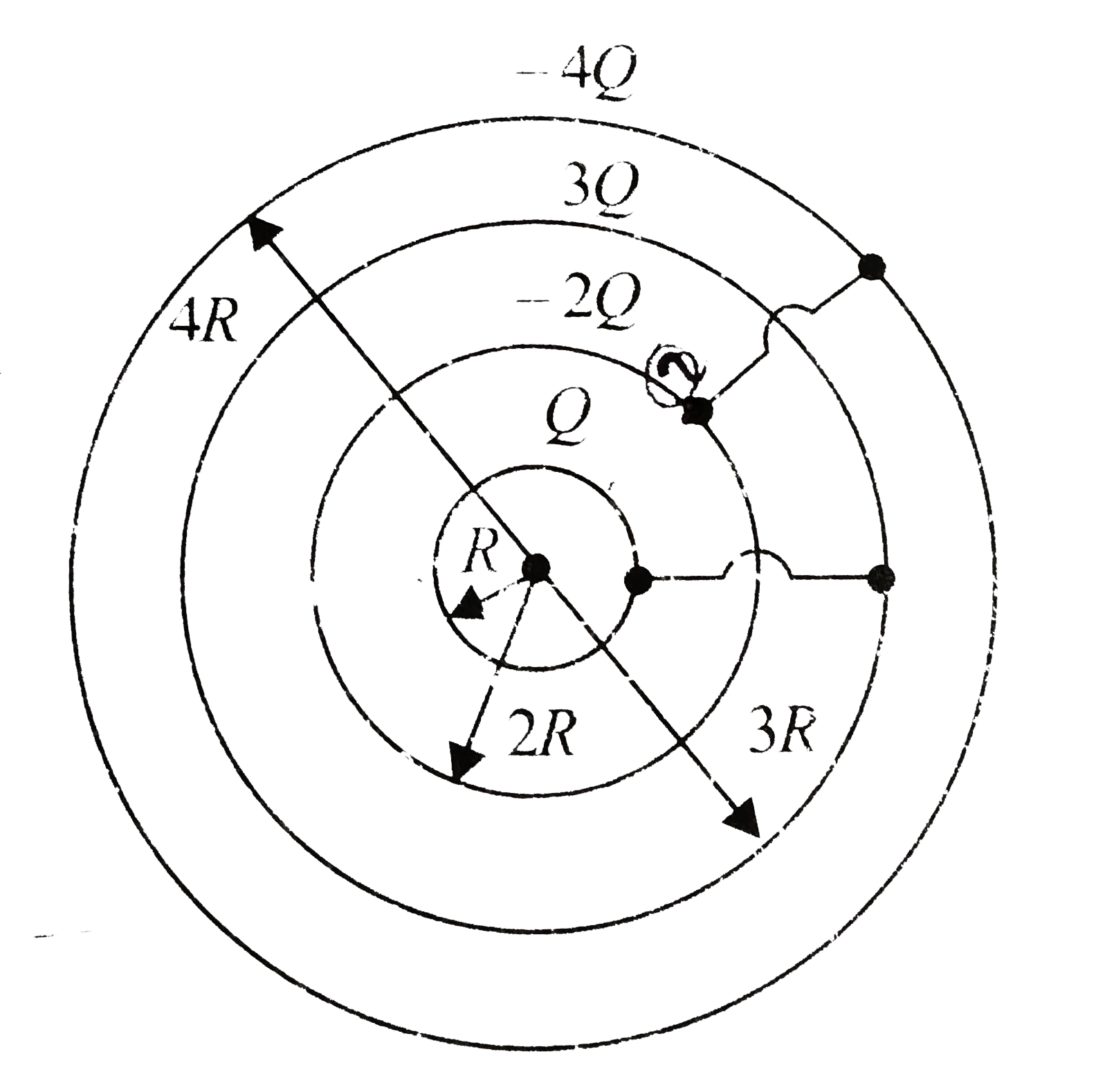
View SolutionFour concentric hollow spheres of radii R, 2R, 3R, and 4R are given the charges as shown in figure. Then the conductors 1 and 3, 2 and 4 are connected by conducting wires (both the connections are made at the same time.)
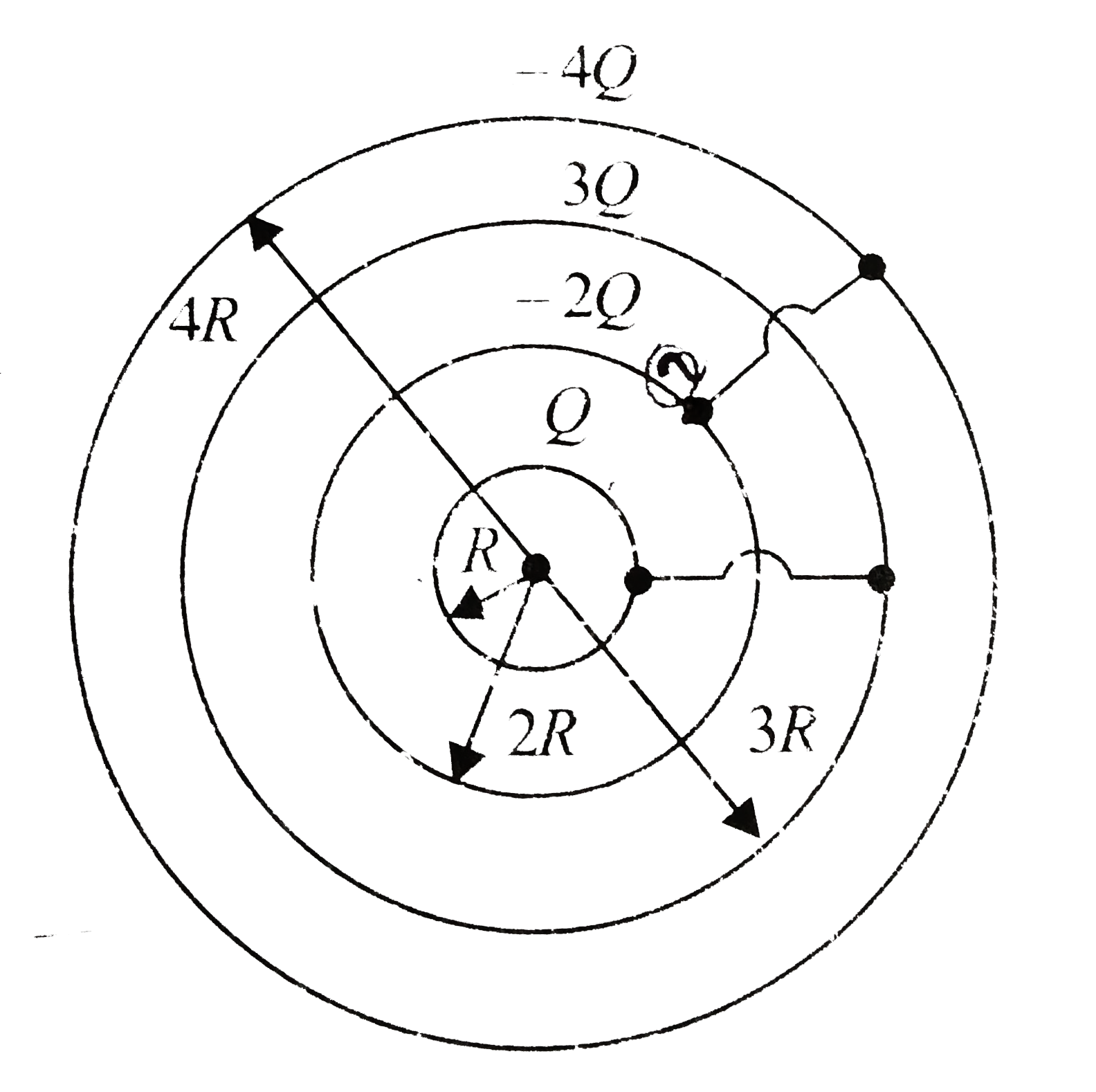 ,
,
The charge on the inner surface of the third conductor is
View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the

View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionTwo concentric spherical conducting shells of radii R and 2R are carrying charges q and 2q, respectively. Both are now connected by a conducting wire. Find the change in electric potential (inV) on the outer shell.
View SolutionConsider two concentric metalic shell's of radii R and 2R. The inner shell is having charge Q and outer shell is uncharged. If they are connected with a conducting wire. Then,
View SolutionTwo spheres of radii R1 and R1 respectively are charged and joined by wire. The ratio of electric field of spheres is
View SolutionTwo metallic spheres of radii 1cm and 2cm are given charges 10−2C and 5×10−2C respectively. If they are connected by a conducting wire, the final charge on the smaller sphere is
View SolutionTwo concentric spherical conducting shells of radii r and R (r<R) carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
View SolutionTwo concentric hollow conducting spheres of radius r and R are shown. The charge on outer shell is Q. what charge should be given to inner sphere so that the potential at any point P outside the outer sphere is zero ?
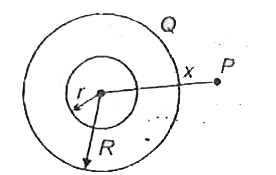
View Solution
