Three equal masses of 1 kg each are placed at the vertices of an equilateral triangle PQR and a mass of 2 kg is placed at the centroid O of the triangle which is at a distance of √2m from each of the vertices of the triangle. The force, in newton, acting on the mass of 2 kg is :
2
√2
1
0
The correct Answer is:D
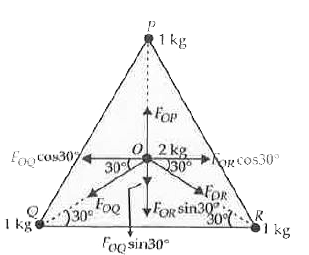
Here OP=OQ=OR=√2m
The gravitational force on mass 2 kg at O due to mass 1 kg at P is
FOP=G×2×1(√2)2 = G along OP
The gravitational force on mass 2 kg at due to mass 1 kg at Q is
FOQ=G×2×1(√2)2= G along OQ
The gravitational force on mass 2 kg at O due to mass 1 kg at R is
FOR=G×2×1(√2)2 = G along OR
Resolving forces FOQ and FOR into its rectangular components. FOQcos30∘ and FORcos30∘ which are equal in magnitude and acting in opposite directions, cancel out each other. The resultant force on the mass 2 kg at O
=FOP−(FOQsin30∘+FORsin30∘)
=G−(G×12+G×12)=0N
Topper's Solved these Questions
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (ACCELERATION DUE TO GRAVITY AND ITS VARIATION WITH ALTITUDE AND DEPTH)
19 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (GRAVITATIONAL POTENTIAL ENERGY AND GRAVITATIONAL POTENTIAL)
6 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (KEPLER.S LAWS OF PLANETARY MOTION)
9 Videos
- BEHAVIOUR OF PERFECT GAS AND KINETIC THEORYBOOK - MTG GUIDECHAPTER - BEHAVIOUR OF PERFECT GAS AND KINETIC THEORYEXERCISE - AIPMT / NEET (MCQs)
11 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - AIPMT/ NEET MCQs
31 Videos
Similar Questions
Three equal masses of 1 kg each are placed at the vertices of an equilateral ΔPQR and a mass of 2kg is placed at the centroid O of the triangle which is at a distance of √2m from each the verticles of the triangle. Find the force (in newton) acting on the mass of 2 kg.
View SolutionThree masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?
View Solution
Knowledge Check
Three equal masses of 2kg each are placed at the vertices of an equilateral triangle and a mass of 4 kg is placed at the centroid of the triangle which is at a distance of √2 m from each of the vertices of the triangle. The force, (in newton) acting on the mass of 4 kg is
A2B√2C1DzeroThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle which is at a distance of sqr(2) m from each of the vertices of the triangle .The force . In newton , acting on the mass of 2 kg is
A2B1C1DZeroThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle of side 1 m, then the gravitational force on one of the masses due to other masses is (approx.)
A{6.67(10−11)}NB10−3 NC[11.5(10−11)]ND[11.5(10−3)]N
Two balls of mass m each are placed at the two vertices of an equilateral triangle. Another ball of mass 2m is placed at the third vertex of the triangle. Locate the centre of mass of the system.
View SolutionThree equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
View SolutionThree equal masses 2m each are placed at the vertices an equilateral triangle PQR
(i) What is the force acting on a mass m placed at the centroid G of the triangle ?
(ii) What is the force on mass m if the mass at the vertex P is quadrupled ?
Take PG = QG = RG = 1m

View SolutionThree masses each of mass m are placed at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is

View SolutionThree particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
View Solution
