Three forces are acting on a particle of mass m initially in equilibrium if the first two forces (→R1and→R2) are perpendicular to each other and suddenly the third force (→R3) is removed, then the magnitude of acceleration of the particle is:
1m∣∣→R2∣∣
1m∣∣→R1+→R2∣∣
1m∣∣→R1−→R2∣∣
1m∣∣→R1∣∣
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the particle and apply Newton's laws of motion. Here’s a step-by-step solution:
Step 1: Understand the initial conditions
The particle of mass m is initially in equilibrium, meaning the net force acting on it is zero. This implies that the sum of all forces acting on the particle is balanced.
Step 2: Identify the forces acting on the particle
We have three forces acting on the particle:
- →R1
- →R2
- →R3
Given that →R1 and →R2 are perpendicular to each other, we can represent them as vectors in a coordinate system.
Step 3: Apply the equilibrium condition
Since the particle is in equilibrium, we have:
→R1+→R2+→R3=0
This means:
→R3=−(→R1+→R2)
Step 4: Remove the third force
Now, if the third force →R3 is suddenly removed, the new net force acting on the particle becomes:
→Fnet=→R1+→R2
Step 5: Calculate the magnitude of the net force
Since →R1 and →R2 are perpendicular, we can use the Pythagorean theorem to find the magnitude of the net force:
|→Fnet|=√|→R1|2+|→R2|2
Step 6: Apply Newton's second law
According to Newton's second law:
→Fnet=m→a
where →a is the acceleration of the particle. Therefore, we can express the acceleration as:
→a=→Fnetm
Step 7: Substitute the net force into the equation
Substituting the expression for the net force, we get:
→a=√|→R1|2+|→R2|2m
Step 8: Determine the magnitude of acceleration
The magnitude of the acceleration is then given by:
|→a|=|→R1|+|→R2|m
Conclusion
Thus, the magnitude of acceleration of the particle after the removal of the third force is:
|→a|=|→R1|+|→R2|m
Final Answer
The correct option is:
1m×|→R1+→R2|
---
The particle of mass m is initially in equilibrium, meaning the net force acting on it is zero. This implies that the sum of all forces acting on the particle is balanced.
We have three forces acting on the particle:
- →R1
- →R2
- →R3
Since the particle is in equilibrium, we have:
→R1+→R2+→R3=0
This means:
→R3=−(→R1+→R2)
Now, if the third force →R3 is suddenly removed, the new net force acting on the particle becomes:
→Fnet=→R1+→R2
Since →R1 and →R2 are perpendicular, we can use the Pythagorean theorem to find the magnitude of the net force:
|→Fnet|=√|→R1|2+|→R2|2
According to Newton's second law:
→Fnet=m→a
where →a is the acceleration of the particle. Therefore, we can express the acceleration as:
→a=→Fnetm
Substituting the expression for the net force, we get:
→a=√|→R1|2+|→R2|2m
The magnitude of the acceleration is then given by:
|→a|=|→R1|+|→R2|m
Thus, the magnitude of acceleration of the particle after the removal of the third force is:
|→a|=|→R1|+|→R2|m
The correct option is:
1m×|→R1+→R2|
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - More than one choice is correct
15 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Assertion- Reason
4 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem for practice
30 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
If →p&→s are not perpendicular to each other and →r&→p=→p×→pand→r.→s=0, then →r=
View SolutionA particle of m=5kg is momentarily at rest at x=att=. It is acted upon by two forces →F1 and →F2. Vec(F)1=70ˆj N. The direction and manitude of →F2 are unknown. The particle experiences a constant acceleration, →a,in the direction as shown in (figure) Neglect gravity.
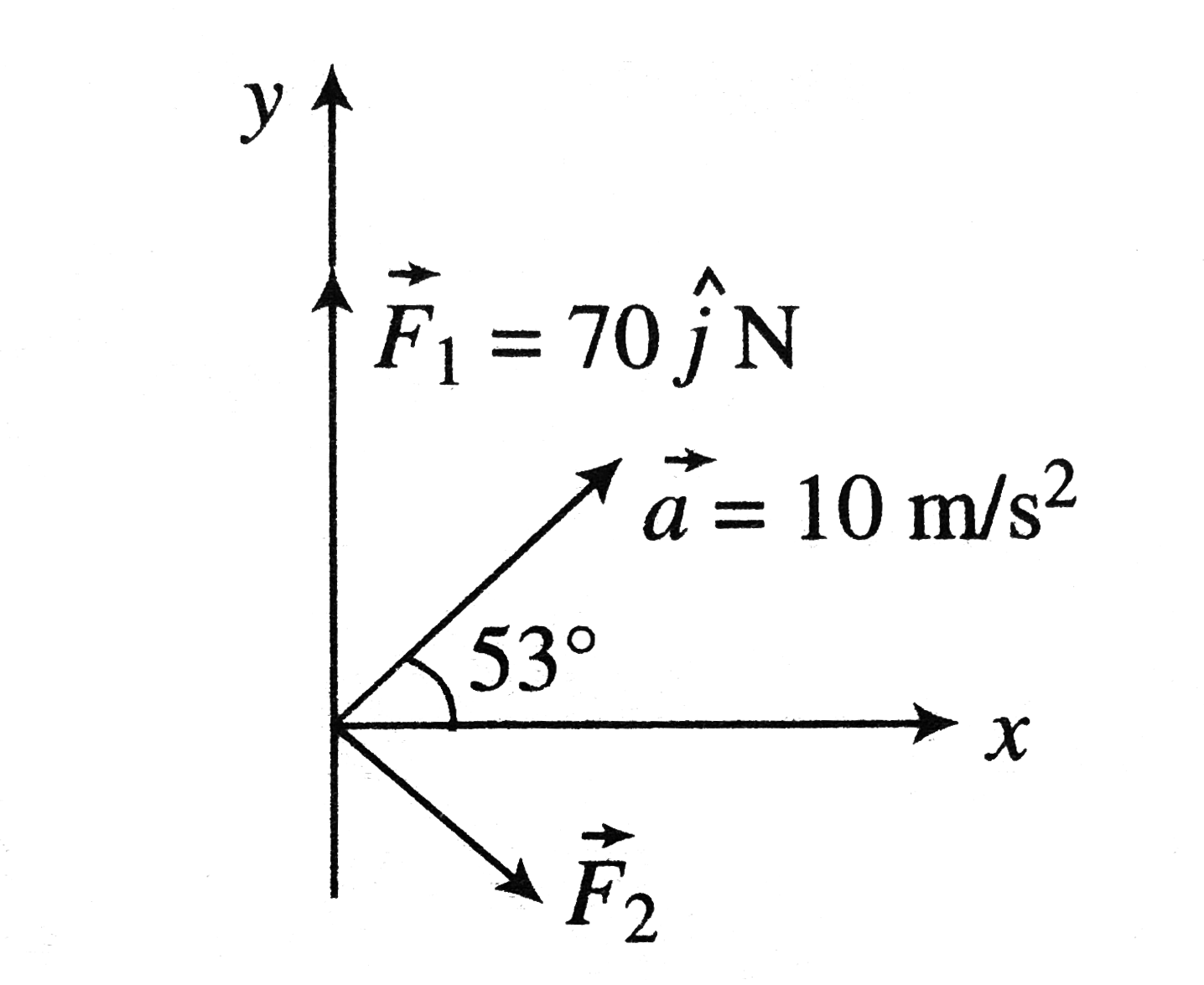
a.Find the missing force →F2.
b. What is the velocity vector of the particle at t=10s?
c. What third force, →F3 is required to make the acceleration of the particle zero? Either give magnitude and direction of →F3 or its components.
View Solution
Knowledge Check
Two forces −→F1and−→F2 are acting at right angles to each other , find their resultant ?
A√F21−F22B√F21+F22C√(F1+F2)DF1+F2When force →F1,→F2,→F3 are acting on a particle of mass m, the particle remains in equilibrium. If the force →F1 is now removed then the acceleration of the particle is :
A→F1/mB→F1/mC→F2−→F3/mD→F2/mWhen force −→F1,−→F2,−→F3…...−→Fn act on a particle , the particle remains in equilibrium . If −→F1 is now removed then acceleration of the particle is
A−→F1mB−−→F1mC−−→F2+−→F3+.....−→Fn−−→F1mD−→F1m
Two forces →F1=3ˆi+4ˆj and →F2=3ˆj+4ˆk are acting simultaneously at a point. What is the magnitude of the resultant force ?
View SolutionWhen forces F1, F2, F3, are acting on a particle of mass m such that F2 and F3 are mutually perpendicular, then the particle remains stationary. If the force F1 is now removed then the acceleration of the particle is
View SolutionThree forces of magnitude 30, 60 and P Newton acting on a particle and particle is in equilibrium. If the angle between the first two forces is 60∘, the value of P is
View SolutionTwo point dipoles of dipole moment →p1and→p2 are at a distance x from each other and →p1∣∣→p2 . The force between the dipoles is :
View SolutionThree forces ¯¯¯¯F1,¯¯¯¯F2and¯¯¯¯F3 are simultaneously acting on a particle of mass 'm' and keep it in equilibrium. If ¯¯¯¯F1 force is reversed in direction only, the acceleration of the particle will be.
View Solution
