When forces F1, F2, F3, are acting on a particle of mass m such that F2 and F3 are mutually perpendicular, then the particle remains stationary. If the force F1 is now removed then the acceleration of the particle is
(a) F/m
(b) F2F3/mF1
(c) (F2−F3)/m
(d) F2/m
The correct Answer is:A
To solve the problem, we need to analyze the forces acting on a particle of mass m and determine the acceleration when one of the forces is removed.
1. Understanding the Forces:
- We have three forces acting on a particle: F1, F2, and F3.
- It is given that F2 and F3 are mutually perpendicular to each other.
2. Condition for Stationarity:
- The particle remains stationary when the net force acting on it is zero. This means that the vector sum of the forces must equal zero:
F1+F2+F3=0
3. Removing F1:
- If we remove F1, the remaining forces are F2 and F3.
- Since F2 and F3 are perpendicular, we can find the resultant force R using the Pythagorean theorem:
R=√F22+F23
4. Applying Newton's Second Law:
- According to Newton's second law, the acceleration a of the particle can be expressed as:
F=m⋅a
- The net force acting on the particle after removing F1 is R:
R=m⋅a
- Therefore, we can express the acceleration as:
a=Rm
5. Substituting for R:
- Now substituting the expression for R:
a=√F22+F23m
6. Relating F1 to F2 and F3:
- From the initial condition where the forces were balanced, we know:
F1=√F22+F23
- Thus, we can substitute F1 into the equation for acceleration:
a=F1m
Final Answer:
The acceleration of the particle after removing F1 is:
a=F1m
- We have three forces acting on a particle: F1, F2, and F3.
- It is given that F2 and F3 are mutually perpendicular to each other.
- The particle remains stationary when the net force acting on it is zero. This means that the vector sum of the forces must equal zero:
F1+F2+F3=0
- If we remove F1, the remaining forces are F2 and F3.
- Since F2 and F3 are perpendicular, we can find the resultant force R using the Pythagorean theorem:
R=√F22+F23
- According to Newton's second law, the acceleration a of the particle can be expressed as:
F=m⋅a
- The net force acting on the particle after removing F1 is R:
R=m⋅a
- Therefore, we can express the acceleration as:
a=Rm
- Now substituting the expression for R:
a=√F22+F23m
- From the initial condition where the forces were balanced, we know:
F1=√F22+F23
- Thus, we can substitute F1 into the equation for acceleration:
a=F1m
The acceleration of the particle after removing F1 is:
a=F1m
Topper's Solved these Questions
- HEAT AND THERMODYNAMICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - HEAT AND THERMODYNAMICSEXERCISE - JEE Main And Advanced
219 Videos
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Videos
Similar Questions
Knowledge Check
When forces F1 , F2 , F3 are acting on a particle of mass m such that F2 and F3 are mutually prependicular, then the particle remains stationary. If the force F1 is now rejmoved then the acceleration of the particle is
AF1/mBF2F3/mF1C(F2−F3)/mDF2/mWhen force →F1,→F2,→F3 are acting on a particle of mass m, the particle remains in equilibrium. If the force →F1 is now removed then the acceleration of the particle is :
A→F1/mB→F1/mC→F2−→F3/mD→F2/mWhen force −→F1,−→F2,−→F3…...−→Fn act on a particle , the particle remains in equilibrium . If −→F1 is now removed then acceleration of the particle is
A−→F1mB−−→F1mC−−→F2+−→F3+.....−→Fn−−→F1mD−→F1m
When a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
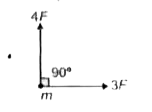
View SolutionFive forces →F1,→F2,→F3,→F4 , and →F5 , are acting on a particle of mass 2.0kg so that is moving with 4m/s2 in east direction. If →F1 force is removed, then the acceleration becomes 7m/s2 in north, then the acceleration of the block if only →F1 is action will be:
View SolutionA particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionThree forces ¯¯¯¯F1,¯¯¯¯F2and¯¯¯¯F3 are simultaneously acting on a particle of mass 'm' and keep it in equilibrium. If ¯¯¯¯F1 force is reversed in direction only, the acceleration of the particle will be.
View Solution
