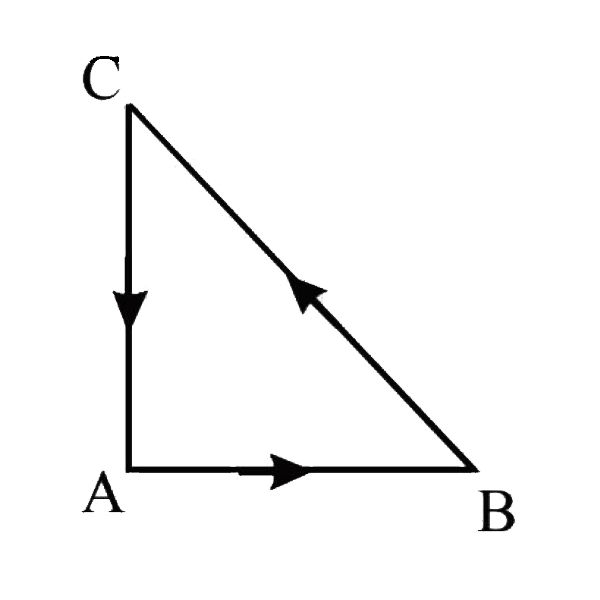
Three forces start acting simultaneously on a particle moving with velocity, ¯v. These forces are respresented in magnitude and direction by the three sides of a triangle ABC. The particle will now move with velocity
→v remaining unchanged
less than →v
greater than →v
→v in the direction of the largest force BC
The correct Answer is:A
Net force =0
Topper's Solved these Questions
Similar Questions
Three forcesstart acting simultaneously on a particle moving with a velocity →v . These forces are represented in magnitude and direction by three sides of a triangle taken in the same order. What now will be the velocity of the particle ?
View SolutionIf an α− particle moving with velocity 'v' enters perpendicular to a magnetic field then the magnetic force acting on it will be-
View Solution
Knowledge Check
Three forces start acting simultaneously on a particle moving with velocity v. These forces are represented in magnitude and direction by the three sides of a triangle ABC (as shown). The particle will now move with velocity.
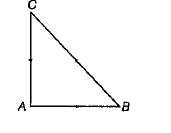 Aless thanBgreater than vCv In the direction of largest force SCDv remaining unchanged
Aless thanBgreater than vCv In the direction of largest force SCDv remaining unchangedThree forces start acting simultaneously on a particle moving the velocity →V. The forces are represented in magnitude and direction by the three sides of a triangle ABC (as shown). The particle will now move with velocity
 Aless than →VBgreater than →VC∣∣→V∣∣ in the direction of largest forceD→V remaining unchanged
Aless than →VBgreater than →VC∣∣→V∣∣ in the direction of largest forceD→V remaining unchangedThree forces start acting simultaneously on a particle moving with velocity, ¯v. These forces are respresented in magnitude and direction by the three sides of a triangle ABC. The particle will now move with velocity
 A→v remaining unchangedBless than →vCgreater than →vD→v in the direction of the largest force BC
A→v remaining unchangedBless than →vCgreater than →vD→v in the direction of the largest force BC
The path of a particle moving under the influence of a force fixed in magnitude and direction is [
View SolutionThe force acting on a particle of charge q moving in a uniform magnets field with velocity v is
View SolutionTwo force in the ratio 1:2 act simultaneously on a particle. The resultant of these forces is three times the first force. The angle between them is
View SolutionForces proportional to AB, BC & 2 CA act along the sides of triangle ABC in order, their resultant represented in magnitude and direction as:
View SolutionForces proportional to AB, BC and 2CA act along the sides of triangle ABC in order, their resultants represented in magnitude and direction is
View Solution
