Three identical particles are located at the vertices of an equilateral triangle. Each particle moves along a meridian with equal speed towards the centroid and collides inelastically. (a) all the three particles will bounce back along the meridians with lesser speed. (b) all the three particles will become stationary. (c) all the particles will continue to move in their original directions but with lesser speed (d) nothing can be said
(a) all the three particles will bounce back along the meridians with lesser speed.
(b) all the three particles will become stationary.
(c) all the particles will continue to move in their original directions but with lesser speed
(d) nothing can be said
The correct Answer is:D
To solve the problem, we need to analyze the situation of the three identical particles moving towards the centroid of an equilateral triangle and their behavior after they collide inelastically.
1. Understanding the Initial Setup:
- We have three identical particles located at the vertices of an equilateral triangle.
- Each particle moves towards the centroid of the triangle with equal speed.
2. Analyzing the Motion Towards the Centroid:
- The centroid of an equilateral triangle is the point where all three medians intersect, and it is located at an equal distance from all three vertices.
- Since all particles are moving towards the centroid, they will meet at this point.
3. Collision Type:
- The problem states that the collision is inelastic. In an inelastic collision, the particles stick together or move as a single entity after the collision.
- The total momentum of the system before the collision must be conserved.
4. Momentum Conservation:
- Before the collision, each particle has a momentum given by p=mv, where m is the mass of each particle and v is their speed.
- The total momentum of the system before the collision is the vector sum of the momenta of the three particles.
5. After the Collision:
- After colliding inelastically, the particles will move together as a single entity.
- The speed of this combined entity can be determined using the conservation of momentum. Since they collide inelastically, they will not bounce back but rather move together with a new speed.
6. Final State:
- Since the particles are identical and collide inelastically, they will not bounce back along their original paths. Instead, they will move together with a speed that is less than the initial speed of the individual particles, but they will not stop completely.
Conclusion:
Given the analysis, the correct answer is:
(c) all the particles will continue to move in their original directions but with lesser speed.
- We have three identical particles located at the vertices of an equilateral triangle.
- Each particle moves towards the centroid of the triangle with equal speed.
- The centroid of an equilateral triangle is the point where all three medians intersect, and it is located at an equal distance from all three vertices.
- Since all particles are moving towards the centroid, they will meet at this point.
- The problem states that the collision is inelastic. In an inelastic collision, the particles stick together or move as a single entity after the collision.
- The total momentum of the system before the collision must be conserved.
- Before the collision, each particle has a momentum given by p=mv, where m is the mass of each particle and v is their speed.
- The total momentum of the system before the collision is the vector sum of the momenta of the three particles.
- After colliding inelastically, the particles will move together as a single entity.
- The speed of this combined entity can be determined using the conservation of momentum. Since they collide inelastically, they will not bounce back but rather move together with a new speed.
- Since the particles are identical and collide inelastically, they will not bounce back along their original paths. Instead, they will move together with a speed that is less than the initial speed of the individual particles, but they will not stop completely.
Given the analysis, the correct answer is:
(c) all the particles will continue to move in their original directions but with lesser speed.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Subjective
Explore 32 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Subjective Questions
Explore 1 Video
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Assertion And Reason
Explore 15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
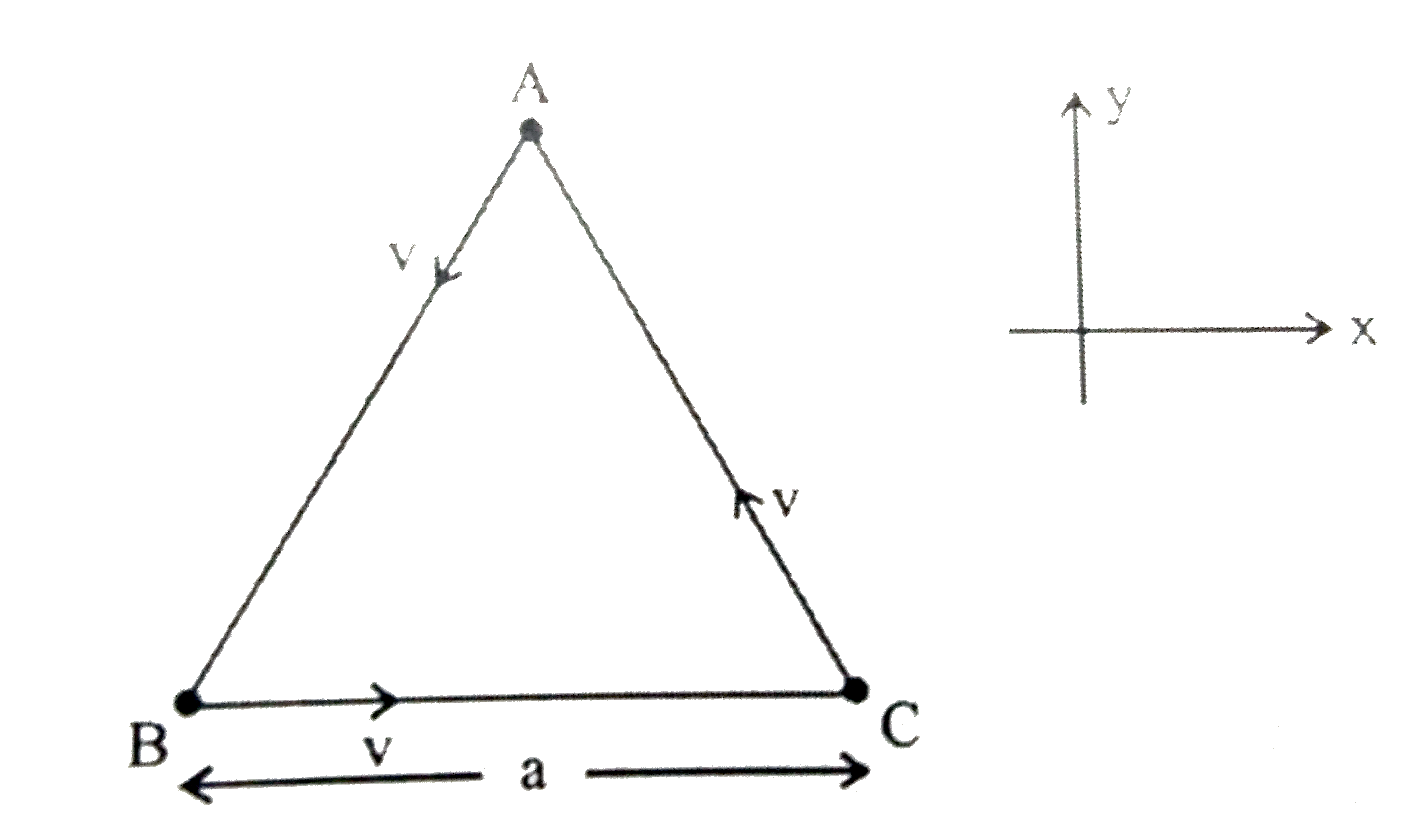
Three particles A, B, Care located at the comers of an equilateral triangle as shown in figure. Each of the particle is moving with velocity v. Then at the instant shown, the relative angular velocity of
View SolutionThree equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
View SolutionThree identical particles each of mass m are placed at the vertices of an equilateral triangle of side a. Fing the force exerted by this system on a particle P of mass m placed at the

(a) the mid point of a side
(b) centre of the triangle
View SolutionThree particles A(50g),B(100g) and C(150g) are placed at vertices of an equilateral triangle as shown in figure. Then the coordinates of center of mass of system is :
_2019_CBT8_E01_014_Q01.png)
View SolutionThree particles A(50g),B(100g) and C(150g) are placed at vertices of an equilateral triangle as shown in figure. Then the coordinates of center of mass of system is :
_2019_CBT8_E01_014_Q01.png)
View SolutionThree particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View SolutionThree particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View SolutionSix particles situated at the corners of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
View SolutionTwo identical particles collide in air inelastically. One moves horizontally and the other moves vertically with equal speed just before collision. The fractional loss in kinetic energy of the system of particles is equal to
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle and other particle of mass 2kg is placed on centroid of triangle which is at a distance of √2 m from each of the vertices of the triangle .The force in newton , acting on the particle of mass 2 kg is
View Solution