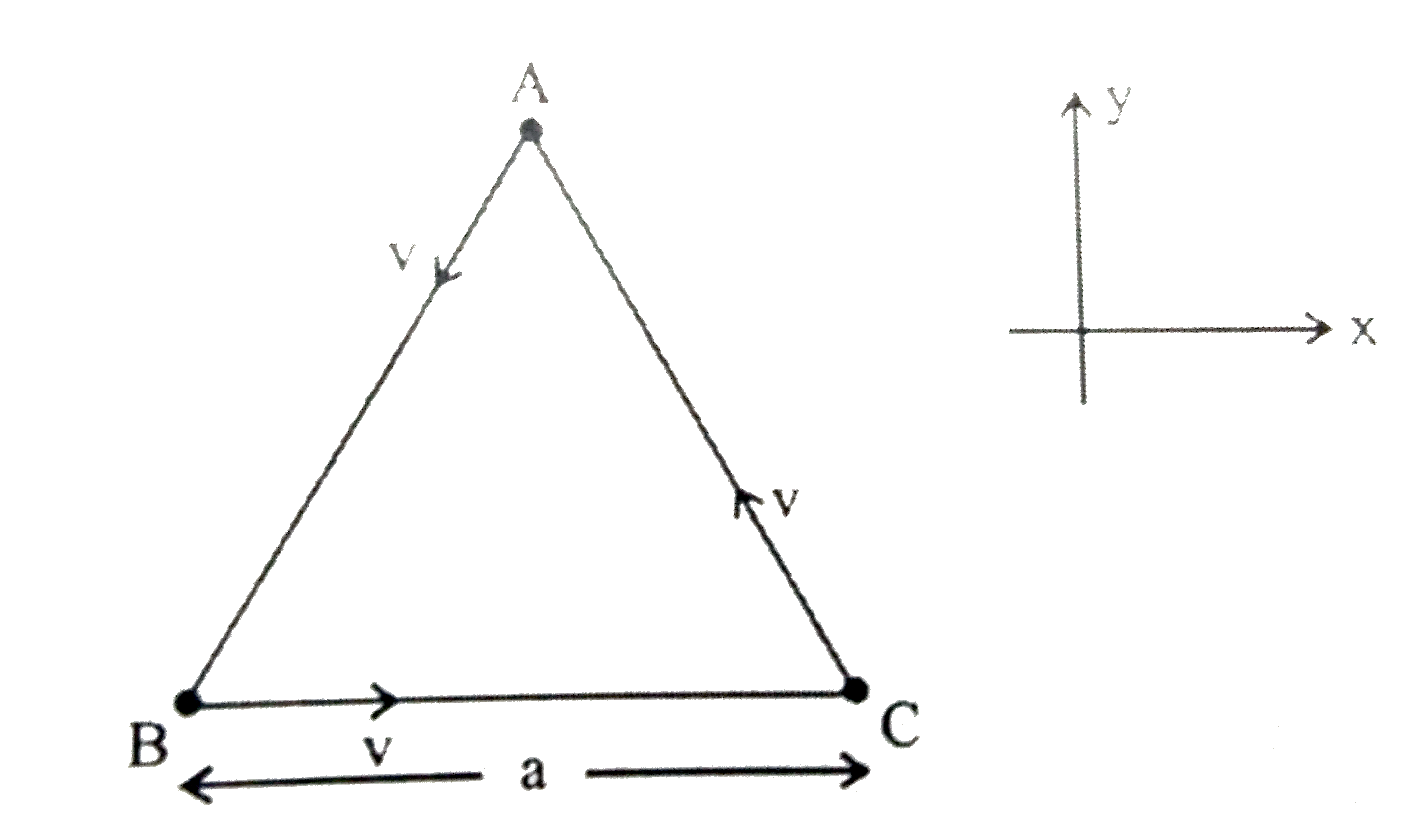
Three particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
The correct Answer is:B, C, D
To solve the problem of when the three particles A, B, and C will meet, we can follow these steps:
Step 1: Understand the Motion of the Particles
Each particle moves with a constant speed v along the edges of the equilateral triangle. Particle A moves towards B, B moves towards C, and C moves towards A.
Step 2: Analyze the Velocity Components
Since the triangle is equilateral, the angle between the direction of motion of each particle and the line connecting them is 60∘.
- The velocity of particle A along AB is v.
- The component of the velocity of particle B towards A (along BA) is vcos(60∘)=v2.
Step 3: Determine the Rate of Decrease of Separation
The separation between particles A and B decreases due to both A moving towards B and B moving towards A. The rate of decrease of separation d between A and B can be calculated as follows:
Rate of decrease of separation=v+v2=3v2
Step 4: Calculate the Time to Meet
The initial distance between particles A and B is d. The time t taken for the particles to meet can be calculated using the formula:
t=DistanceRate=d3v2=2d3v
Conclusion
Thus, the time at which all three particles will meet is:
t=2d3v
Each particle moves with a constant speed v along the edges of the equilateral triangle. Particle A moves towards B, B moves towards C, and C moves towards A.
Since the triangle is equilateral, the angle between the direction of motion of each particle and the line connecting them is 60∘.
- The component of the velocity of particle B towards A (along BA) is vcos(60∘)=v2.
The separation between particles A and B decreases due to both A moving towards B and B moving towards A. The rate of decrease of separation d between A and B can be calculated as follows:
The initial distance between particles A and B is d. The time t taken for the particles to meet can be calculated using the formula:
Thus, the time at which all three particles will meet is:
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Exercise 6.1
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Exercise 6.2
3 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Example Type 7
1 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Four particles A,B,CandD are situated at the corner of a square ABCD of side a at t-0. Each of particles moves with constant speed (v). A always has its velocity along AB,B along BC,C along CD~andD along DA. At what time will these particles meet each other ?
View SolutionThree particles A, B, Care located at the comers of an equilateral triangle as shown in figure. Each of the particle is moving with velocity v. Then at the instant shown, the relative angular velocity of
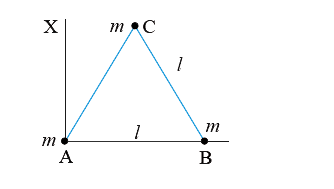
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L as shown in the figure. Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

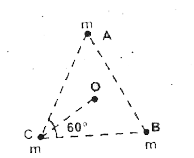
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
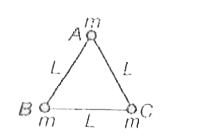
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
Force acting on particle C, due to particle A and B
View SolutionThree particles A,B and C each of mass m are lying at the corners of an equilateral triangle of side L . If the particle A is released keeping the particles B and C fixed , the magnitude of instantaneous acceleration of A is
View SolutionThree identical particles each of mass m are placed at the vertices of an equilateral triangle of side a. Fing the force exerted by this system on a particle P of mass m placed at the

(a) the mid point of a side
(b) centre of the triangle
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionFind the centre of mass of three particle at the vertices of an equilateral triangle. The masses of the particle are 100g,150g,and200g respectively. Each side of the equilateral triangle is 0.5m along.
View SolutionThree identical particles are located at the vertices of an equilateral triangle. Each particle moves along a meridian with equal speed towards the centroid and collides inelastically. (a) all the three particles will bounce back along the meridians with lesser speed. (b) all the three particles will become stationary. (c) all the particles will continue to move in their original directions but with lesser speed (d) nothing can be said
View Solution
