Four particles A,B,CandD are situated at the corner of a square ABCD of side a at t-0. Each of particles moves with constant speed (v). A always has its velocity along AB,B along BC,C along CD~andD along DA. At what time will these particles meet each other ?
The correct Answer is:alv
To solve the problem of when the four particles A, B, C, and D will meet at the center of the square ABCD, we can follow these steps:
Step 1: Understand the motion of the particles
Each particle is moving with a constant speed v along the sides of the square. Particle A moves along side AB, B along BC, C along CD, and D along DA.
Step 2: Identify the meeting point
The particles will meet at the center of the square, which we can denote as point O. The coordinates of point O can be determined as it is the midpoint of the diagonals of the square.
Step 3: Calculate the distance from a corner to the center
The distance from any corner of the square (say A) to the center O can be calculated using the Pythagorean theorem. Since the side of the square is a, the distance AO is:
AO=√(a2)2+(a2)2=√a24+a24=√a22=a√2
Step 4: Determine the effective velocity towards the center
Since particle A is moving towards the center O at an angle of 45 degrees, we can find the component of its velocity in the direction of AO. The effective velocity component vAO can be calculated as:
vAO=vcos(45∘)=v⋅1√2=v√2
Step 5: Calculate the time taken to meet at the center
Using the formula for time, t=distancevelocity, we can find the time taken by particle A to reach point O:
t=AOvAO=a√2v√2=av
Conclusion
Thus, the time at which all four particles will meet at the center O is:
t=av
Each particle is moving with a constant speed v along the sides of the square. Particle A moves along side AB, B along BC, C along CD, and D along DA.
The particles will meet at the center of the square, which we can denote as point O. The coordinates of point O can be determined as it is the midpoint of the diagonals of the square.
The distance from any corner of the square (say A) to the center O can be calculated using the Pythagorean theorem. Since the side of the square is a, the distance AO is:
AO=√(a2)2+(a2)2=√a24+a24=√a22=a√2
Since particle A is moving towards the center O at an angle of 45 degrees, we can find the component of its velocity in the direction of AO. The effective velocity component vAO can be calculated as:
vAO=vcos(45∘)=v⋅1√2=v√2
Using the formula for time, t=distancevelocity, we can find the time taken by particle A to reach point O:
t=AOvAO=a√2v√2=av
Thus, the time at which all four particles will meet at the center O is:
t=av
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -A Objective (one option is correct)
50 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -B Objective (one option is correct)
29 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - llustration 1 :
1 Videos
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
Three particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View SolutionThree particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View SolutionFour persons A, B, C and D initially at the corners of a square of side of length d. If every person starts moving with same speed v such that each one faces the other always, the person will meet after time
View SolutionSix particles situated at the corners of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
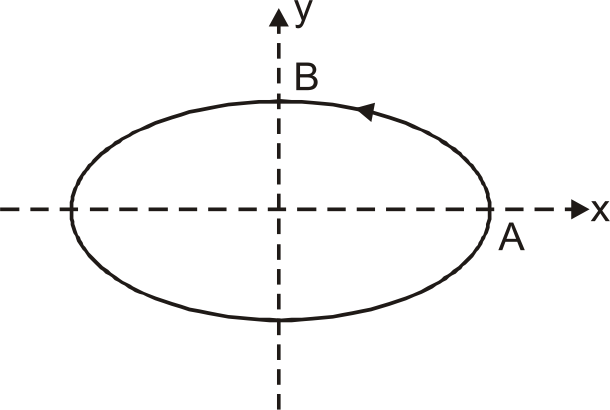
View SolutionA particle is moving along an elliptical path with constant speed. As it moves from A to B, magnitude of its acceleration :
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionFour particles of masses 2,2,4,4 kg are arranged at the corners A,B,C,D of a square ABCD of side 2m as shown in the figure. The perpendicular distance of their centre of mass from the side AB is

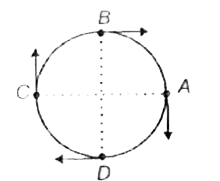
View SolutionFour particles A, B, C and D are moving with constant speed v each at the instant shown relative velocity of A with respect to B, C and D are in directions
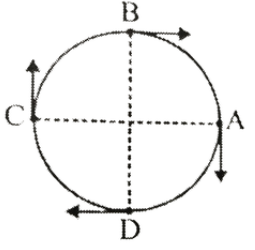
View SolutionFour particles A, B, C and D are moving with constant speed v each. At the instant shown relative velocity of A with respect to B, C and D are in directions :-
View SolutionFour charges are arranged at the corners of a square ABCD, as shown. The force on a positive charge kept at the centre of the square is
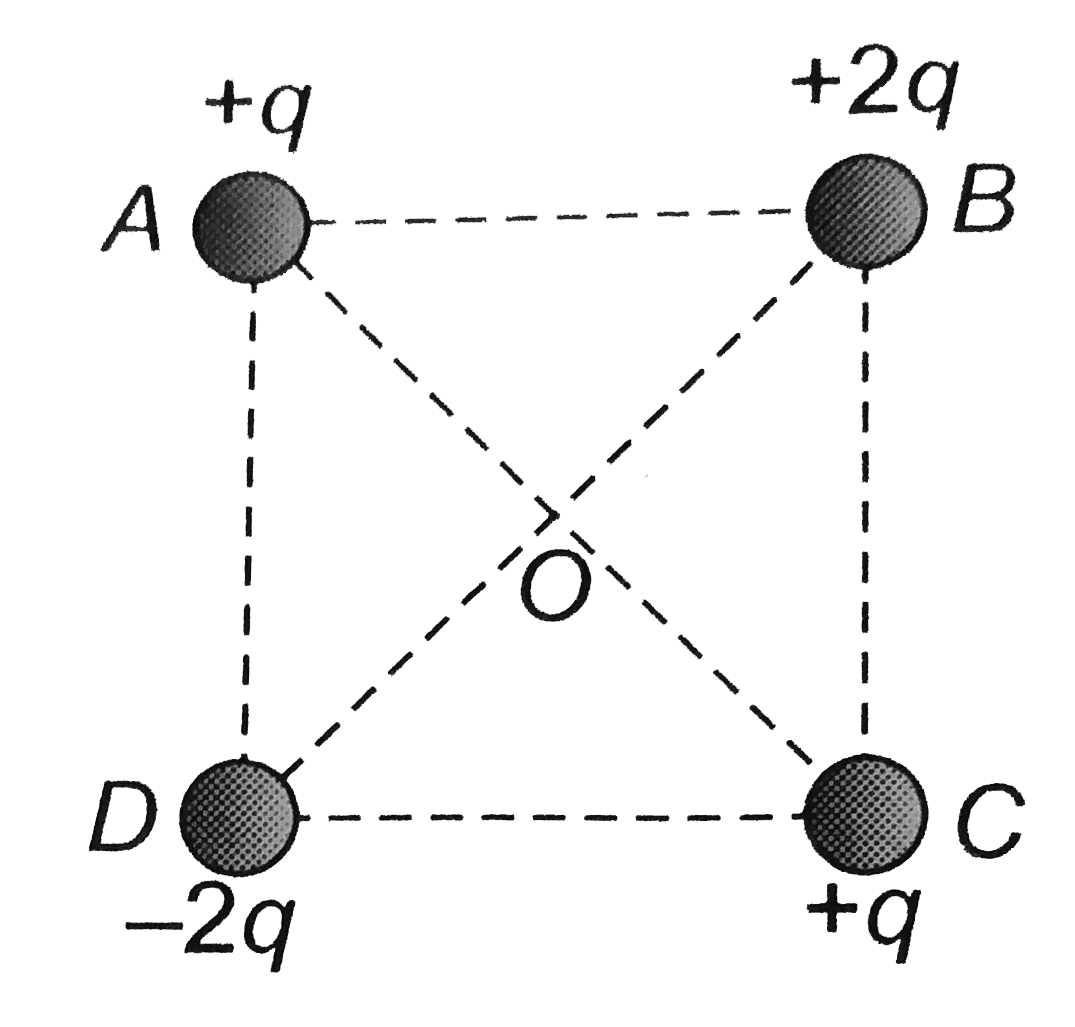
(A)zero (B)along diagonal AC
(C)along diagonal BD (D)perpendicular to the side AB
View Solution
