Three rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.
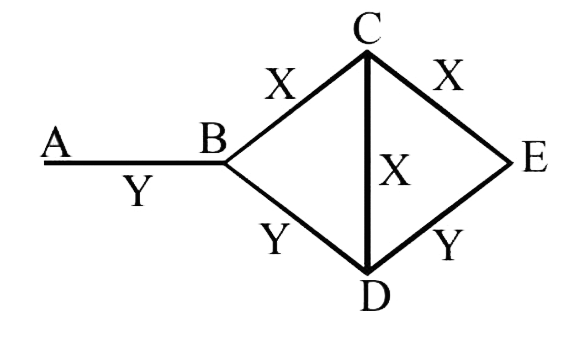
Let Kx and Ky be the thermal conductivites of X and Y respectively, and let TB,TC and TD be the temperature of junctions B,C and D, respectively Given TA=60∘C and TE=10∘C. In order to solve this problem, we will apply the principle that, in the steady state, the rate at which heat enters a junction is equal to the rate at which heat leaves that junction. In Fig. 1.63, the direction of flow of heat is given by arrows.
For junction B, we have

KyA(TA−TB)d=KxA(TB−TC)d+KyA(TB−TC)d
or Ky(TA−TB)=Kx(TB−TC)+Ky(TB−TD)
or (TA−TB)=KxKy(TB−TC)+Ky(TB−TD)
Given KxKy=9.2×10−24.6×10−2=2 and TA=60∘C. Therefore
(60−TB)=2(TB−TC)+(TB−TC)+(TB−TD)
or 4TB−2TC−TD=60 (i)
For junction C, we have
KxA(TB−TC)d=KxA(TC−TD)d+KxA(TC−TB)d
Solving we get
−TB+3TC−TD=10[AtTE=10∘C] (ii)
For junction D, we have
or KyA(TB−TD)d+KxA(TC−TD)d=KyA(TD−TE)d
or (TB−TD)+KxKy=2 and TE=10∘C. In this equation, we have
(TB−TD)+2(TC−TD)=(TD−10)
TB+2TC−4TD=−10 (iii)
Solving Eqs. (i),(ii) and (iii), we get
TB=30∘C and TC=TD=20∘C
Topper's Solved these Questions
Similar Questions
Three rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C , calculate the temperature of the junction B. The thermal conductivity of x is 800Wm−1C−1 and that of y is 400Wm−1C−1 .

View SolutionThree rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C , calculate the temperature of the junction B. The thermal conductivity of x is 800Wm−1.∘C−1 and that of y is 400Wm−1.∘C−1 .

View Solution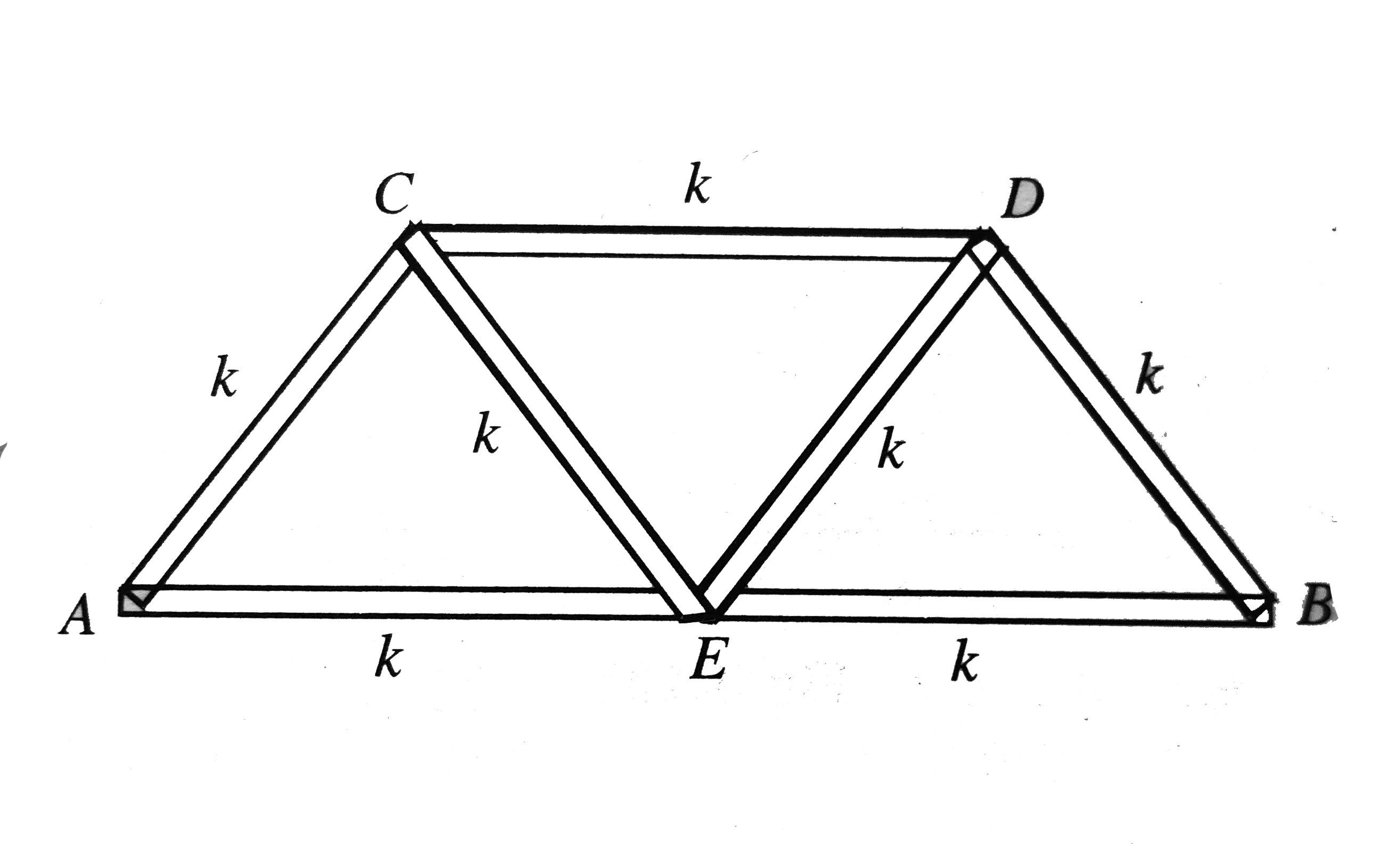
Seven identical rods of material of thermal conductivity k are connected as shown in Fig. All the rods are of identical length l and cross sectional area A If the one end A is kept at 100∘C and the other end is kept at 0∘C what would be the temperatures of the junctions C, D and E(θC,θ)D and θE) in the steady state?
View SolutionFour rods of material X and three rods of material Y are connected as shown in figure. All the rods are of identical lengths and cross-sectional area. Given thermal resistance of rod of material X,Rx=R and thermal conductivities of materials are related by relation KY=2KX.
_E01_157_Q01.png)
Column-IColumn-II(A)Thermal resistance between B and E(p)50013.∘C(B)Thermal resistance between A and F(q)70013.∘C(C)Temperature of junction B(r)2R3(D)Temperature of junction D(s)13R6
View SolutionThe ends of copper rod of length 1m and area of cross section 1cm2 are maintained at 0∘C and 100∘C. At the centre of rod, there is a source of heat of 32W. The thermal conductivity of copper is 400W/mK

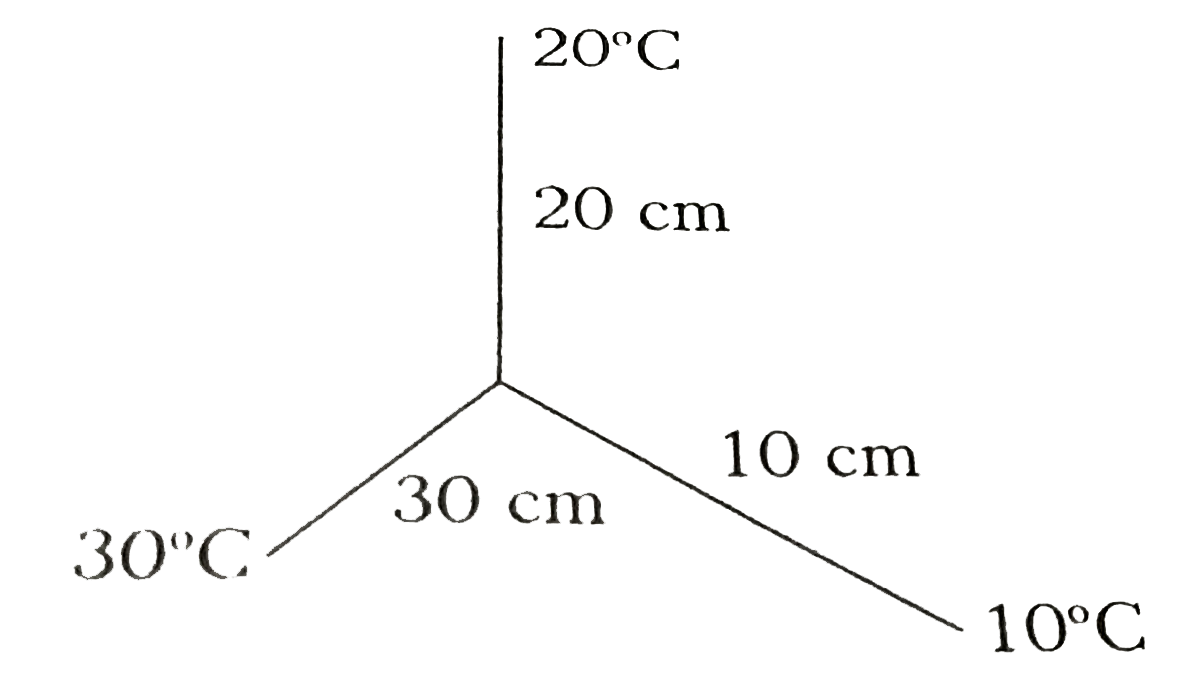
View SolutionThree rods made of the same material and having same cross-section area but different length 10 cm, 20 cm and 30 cm are joined as shown. The temperature of the junction is
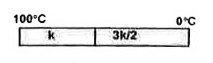
View SolutionTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is
View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390Wm−1C−1 and that of steel =46Wm−1C−1 .

View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390WM−1.∘C−1 and that of steel =46Wm−1.∘C−1 .

View SolutionThree rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.
There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.
View Solution
