Torricelli's barometer used mercury. Pascal duplicated it using French wine of density 984kgm−3. Determine the height of the wine column for normal atmospheric pressure.
To solve the problem of determining the height of the wine column in Pascal's barometer, we can follow these steps:
Step 1: Understand the relationship between pressure, density, and height
The pressure exerted by a column of liquid is given by the formula:
P=ρgh
where:
- P is the pressure,
- ρ is the density of the liquid,
- g is the acceleration due to gravity (approximately 9.81m/s2),
- h is the height of the liquid column.
Step 2: Identify the known values
For mercury:
- Density of mercury, ρHg=13.6×103kg/m3
- Height of mercury column for normal atmospheric pressure, hHg=0.76m
For French wine:
- Density of French wine, ρwine=984kg/m3
Step 3: Set up the equation for pressure balance
For the mercury column and the wine column, the pressures must be equal at atmospheric pressure:
ρHgghHg=ρwineghwine
Step 4: Cancel out g from both sides
Since g is present on both sides of the equation, we can cancel it out:
ρHghHg=ρwinehwine
Step 5: Solve for the height of the wine column
Rearranging the equation to find hwine:
hwine=ρHghHgρwine
Step 6: Substitute the known values
Now we can substitute the known values into the equation:
hwine=(13.6×103kg/m3)(0.76m)984kg/m3
Step 7: Calculate the height of the wine column
Calculating the above expression:
hwine=(13.6×103)(0.76)984
hwine=10345.6984
hwine≈10.5m
Final Answer
The height of the wine column for normal atmospheric pressure is approximately 10.5m.
---
The pressure exerted by a column of liquid is given by the formula:
P=ρgh
where:
- P is the pressure,
- ρ is the density of the liquid,
- g is the acceleration due to gravity (approximately 9.81m/s2),
- h is the height of the liquid column.
For mercury:
- Density of mercury, ρHg=13.6×103kg/m3
- Height of mercury column for normal atmospheric pressure, hHg=0.76m
- Density of French wine, ρwine=984kg/m3
For the mercury column and the wine column, the pressures must be equal at atmospheric pressure:
ρHgghHg=ρwineghwine
Since g is present on both sides of the equation, we can cancel it out:
ρHghHg=ρwinehwine
Rearranging the equation to find hwine:
hwine=ρHghHgρwine
Now we can substitute the known values into the equation:
hwine=(13.6×103kg/m3)(0.76m)984kg/m3
Calculating the above expression:
hwine=(13.6×103)(0.76)984
hwine=10345.6984
hwine≈10.5m
The height of the wine column for normal atmospheric pressure is approximately 10.5m.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE
31 Videos
- LAWS OF MOTION BOOK - NCERT ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - EXERCISE
40 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE
21 Videos
Similar Questions
Knowledge Check
Torricelli's barometer used mercury but pascal duplicated it using French wine of density 984kgm−3 . In that case, the height of the wine column for normal atmospheric pressure is
(Take the density of mercury =1.36×103kgm−3)A5.5 mB10.5 mC9.8 mD15 m
What would be the height of column in barometer if water (density=1000Kg/m3) is used instead of mercury for measuring atmospheric pressure?
View SolutionExplain how is the height of mercury column in the tube of a simple barometer, a measure of the atmospheric pressure.
View Solution(a) Calculate the height of a water column which will exert on its base the same pressure as the 70 cm column of mercury. Density of mercury is 13.6gcm−3
(b) Will the height of the water column in part (a) change if the cross section of the water column is made wider ?
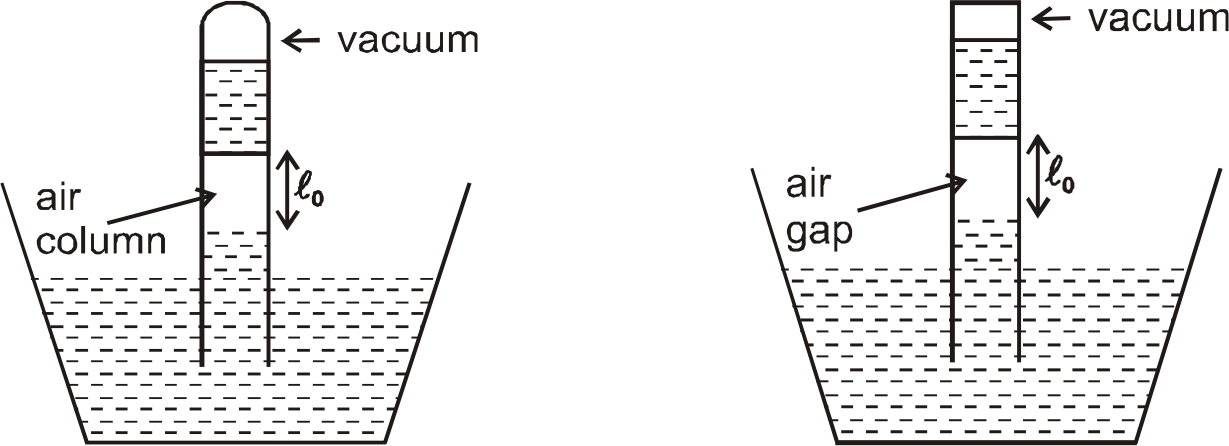
View SolutionAt the middle of the mercury barometer tube there is a little column of air with the length l0 and there is vacuum at the top as shown. Under the normal atmospheric pressure and the temperature of 200 le,vom/ l0=10cm. What will be the length of the air column if the temperature rises to 330 kelvin? (Neglict expansion of the tube)
View SolutionA barometer correctly reads the atmospheric pressure as 76cm of mercury. Water droplets are slowly introduced into the barometer tube by a dropper. The height of the mercury column first decreases and then become constant. If the saturation vapour pressure at the atmospheric temperature is 0.80cm of mercury, find the height if the mercury column when it reaches its minimum value.
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .
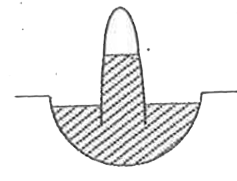
If this expriment uses water instead of mercury , then
A. length of water will be equal to 76 cm
B. length of water will be less than 76 cm
C. length of water will be greater than 76 cm
D. none of the above
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .
If an additional hole is also made at P ' at the top point of the tube , then

A. mercury will not come out of the tube
B. mercury may come out of the tube after some time .
C. mercury will come out of the tube instantly
D. none of these
View Solution
