Trajectory of a particle in a projectile motion is given as . Here and are in metre. For this projectile motion the following with .
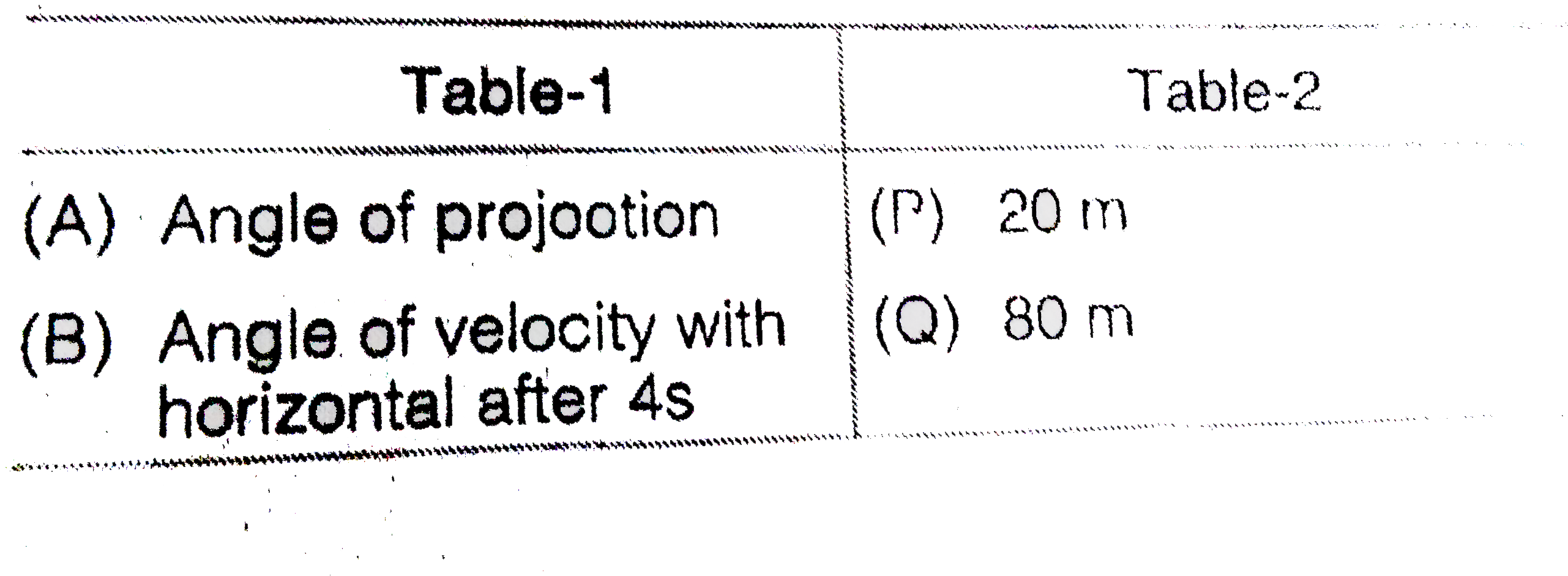
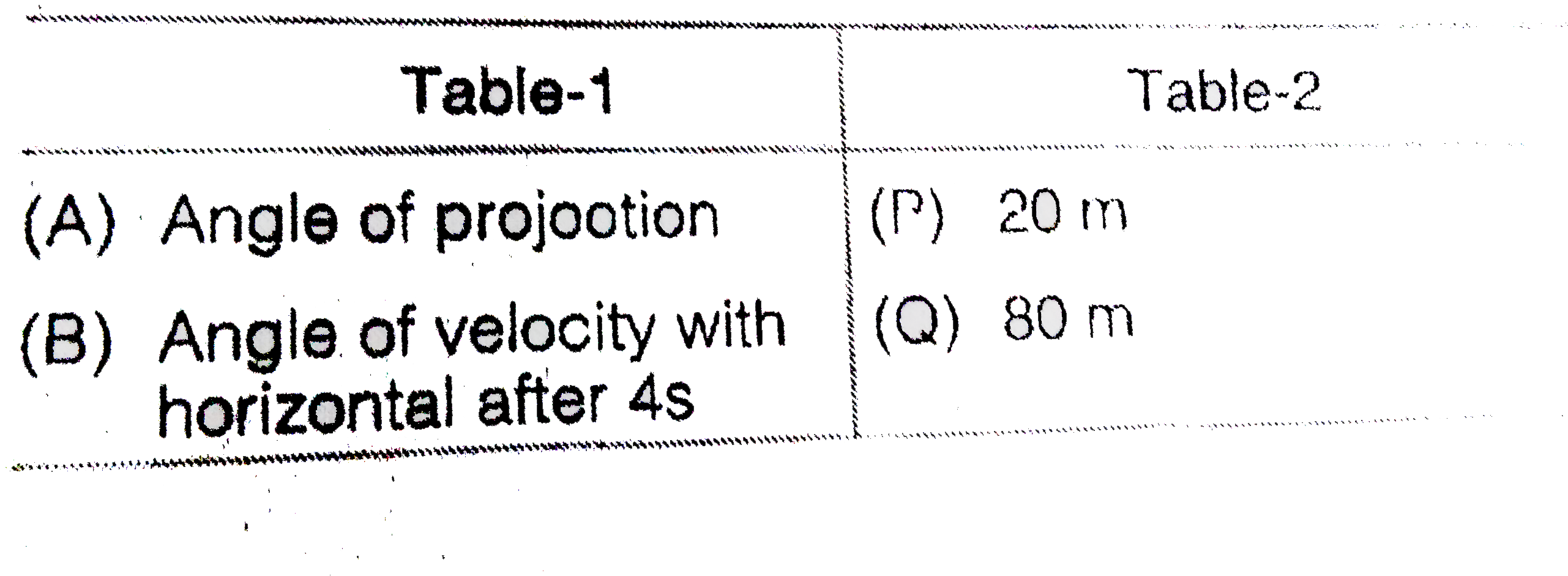
The correct Answer is:A, B, C, D
Step by step video & image solution for Trajectory of a particle in a projectile motion is given as y=x-(x^(2))/80. Here x and y are in metre. For this projectile motion the following with g=10m//s^(2). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - COMPREHENSION_TYPE
13 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Trajectory of particle in a projectile motion is given as y=x−x280. Here, x and y are in meters. For this projectile motion, match the following with g=10m/s2.
Column-IColumn-II(A)Angle of projection (in degrees)(P)20(B)Angle of velocity with horizontal after 4s (in degrees)(Q)80(C)Maximum height (in meters)(R)45(D)Horizontal range (in meters)(S)30(T)60
View SolutionTrajectory of particle in a projectile motion is given as y=x−x280. Here x and y are in metre. For this projectile motion match the following with g=10ms−2.

View SolutionThe potential energy (in joules ) function of a particle in a region of space is given as:
U=(2x2+3y2+2x)
Here x,y and z are in metres. Find the maginitude of x compenent of force ( in newton) acting on the particle at point P ( 1m, 2m, 3m).
View SolutionThe displacement x of a particle in a straight line motion is given by x=1−t−t2. The correct representation of the motion is
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Time of flight of the projectile is :-
View SolutionIf y=x−x2 is the path of a projectile, then which of following is incorrect (g=10m/s2):
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
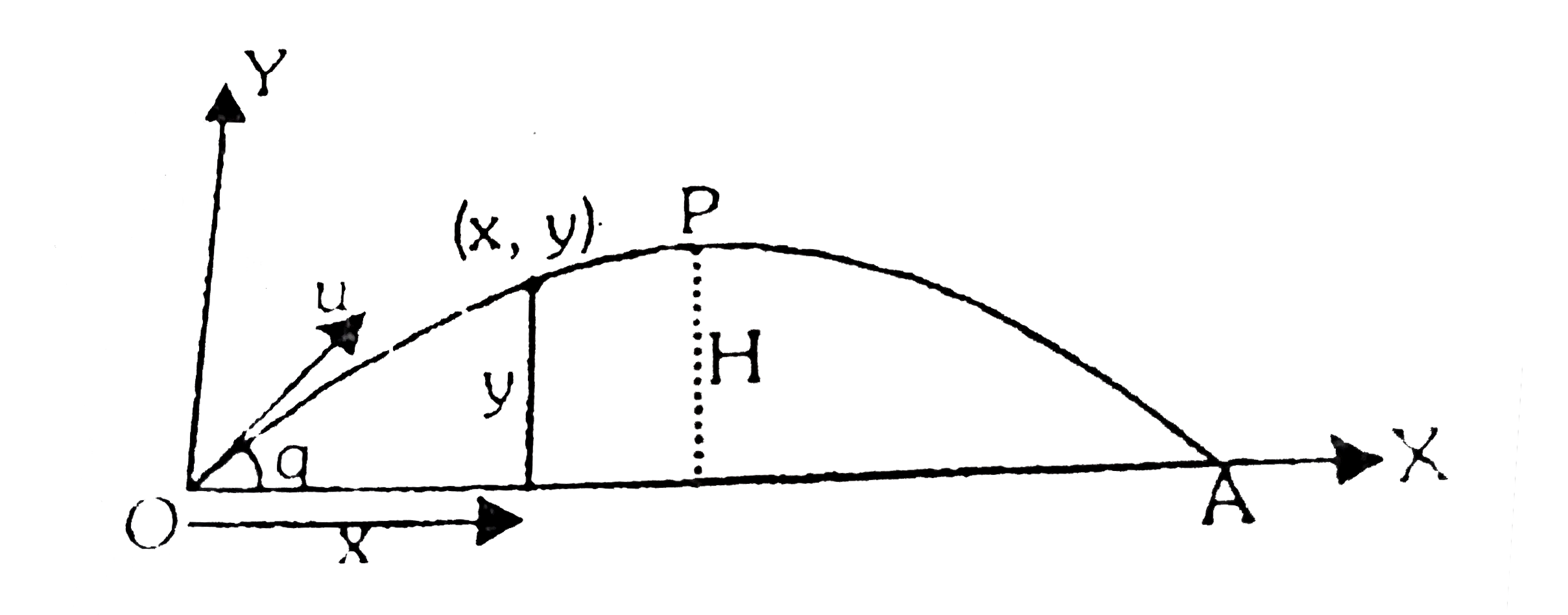
Range OA is :-
View SolutionEquation of trajectory of a projectile is given by y=−x2+10x where x and y are in meters and x is along horizontal and y is vericall y upward and particle is projeted from origin. Then : (g=10)m/s2
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Angle of projection θ is :-
View SolutionAcceleration of a particle under projectile motion at the highest point of its trajectory is :
View Solution
