Equation of trajectory of a projectile is given by y=−x2+10x where x and y are in meters and x is along horizontal and y is vericall y upward and particle is projeted from origin. Then : (g=10)m/s2
initial velocity of particle is √505m/s
horizontal range is 10m
maximum height is 25m
angle of projection with horizontal is tan−1(5).
The correct Answer is:A, B, C
To solve the problem, we need to analyze the given equation of the trajectory of a projectile, which is given by:
y=−x2+10x
Step 1: Find the horizontal range
The horizontal range is the value of x when y=0.
Set y=0:
0=−x2+10x
Rearranging gives:
x2−10x=0
Factoring out x:
x(x−10)=0
Thus, x=0 or x=10.
So, the horizontal range R is:
R=10meters
Step 2: Find the maximum height
To find the maximum height, we need to determine the vertex of the parabola represented by the equation. The vertex x coordinate can be found using the formula:
x=−b2a
where a=−1 and b=10:
x=−102⋅−1=5
Now, substitute x=5 back into the equation to find y:
y=−52+10⋅5=−25+50=25
Thus, the maximum height H is:
H=25meters
Step 3: Find the initial velocity and angle of projection
We can use the formula for maximum height:
H=u2sin2θ2g
Given H=25meters and g=10m/s2:
25=u2sin2θ2⋅10
This simplifies to:
25=u2sin2θ20
Multiplying both sides by 20:
500=u2sin2θ
Thus:
usinθ=√500=10√5
Step 4: Find the slope at the origin
The slope of the trajectory at any point can be found by differentiating y with respect to x:
dydx=−2x+10
At the origin (0,0):
dydx∣∣∣(0,0)=−2(0)+10=10
Thus, the slope tanθ=10, which gives:
θ=tan−1(10)
Step 5: Find sinθ
Using the triangle formed by the slope:
Opposite=10,Adjacent=1
The hypotenuse h is:
h=√102+12=√101
Thus:
sinθ=10√101
Step 6: Substitute back to find u
Substituting sinθ into usinθ=10√5:
u⋅10√101=10√5
Solving for u:
u=10√5⋅√10110=√505
Summary of Results
1. Horizontal Range R=10meters
2. Maximum Height H=25meters
3. Initial Velocity u=√505m/s
4. Angle of Projection θ=tan−1(10)
The horizontal range is the value of x when y=0.
0=−x2+10x
Rearranging gives:
x2−10x=0
Factoring out x:
x(x−10)=0
Thus, x=0 or x=10.
R=10meters
To find the maximum height, we need to determine the vertex of the parabola represented by the equation. The vertex x coordinate can be found using the formula:
x=−b2a
where a=−1 and b=10:
x=−102⋅−1=5
y=−52+10⋅5=−25+50=25
H=25meters
We can use the formula for maximum height:
H=u2sin2θ2g
Given H=25meters and g=10m/s2:
25=u2sin2θ2⋅10
This simplifies to:
25=u2sin2θ20
Multiplying both sides by 20:
500=u2sin2θ
Thus:
usinθ=√500=10√5
The slope of the trajectory at any point can be found by differentiating y with respect to x:
dydx=−2x+10
At the origin (0,0):
dydx∣∣∣(0,0)=−2(0)+10=10
θ=tan−1(10)
Using the triangle formed by the slope:
Opposite=10,Adjacent=1
The hypotenuse h is:
h=√102+12=√101
Thus:
sinθ=10√101
Substituting sinθ into usinθ=10√5:
u⋅10√101=10√5
Solving for u:
u=10√5⋅√10110=√505
1. Horizontal Range R=10meters
2. Maximum Height H=25meters
3. Initial Velocity u=√505m/s
4. Angle of Projection θ=tan−1(10)
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 2
20 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
The equation of trajectory ofa projectile is y=10x−59x2 If we assume g=10ms−2, the range of projectile (in metre) is
View SolutionThe trajectory of a projectile in a vertical plane is y=ax−bx2, where aandb are constant and xandy are, respectively, horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projectile from the horizontal are.
View SolutionThe trajectory of a projectile in a vertical plane is y=ax−bx2, where aandb are constant and xandy are, respectively, horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projectile from the horizontal are.
View SolutionThe wave described by y =0.25sin(10πx−2πt) where x and y are in meters and t in seconds , is a wave travelling along the
View SolutionThe equation of a simple harmonic wave is given by
y=3sinπ2(50t−x)
where x and y are in meters and x is in second .The ratio of maximum particle velocity to the wave velocity is
View SolutionThe equation of a simple harmonic wave is given by
y=3sinπ2(50t−x)
where x and y are in meters and x is in second .The ratio of maximum particle velocity to the wave velocity is
View SolutionThe equation of trajectory of an oblique projectile y=√3x−gx22. The angle of projection is
View SolutionA wave equation which gives the displacement along the y-direction is given by y=10−4sin(60t+2x) where xandy are in meters and t is time in seconds. This represents a wave
View SolutionTrajectory of particle in a projectile motion is given as y=x−x280. Here x and y are in metre. For this projectile motion match the following with g=10ms−2.

View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
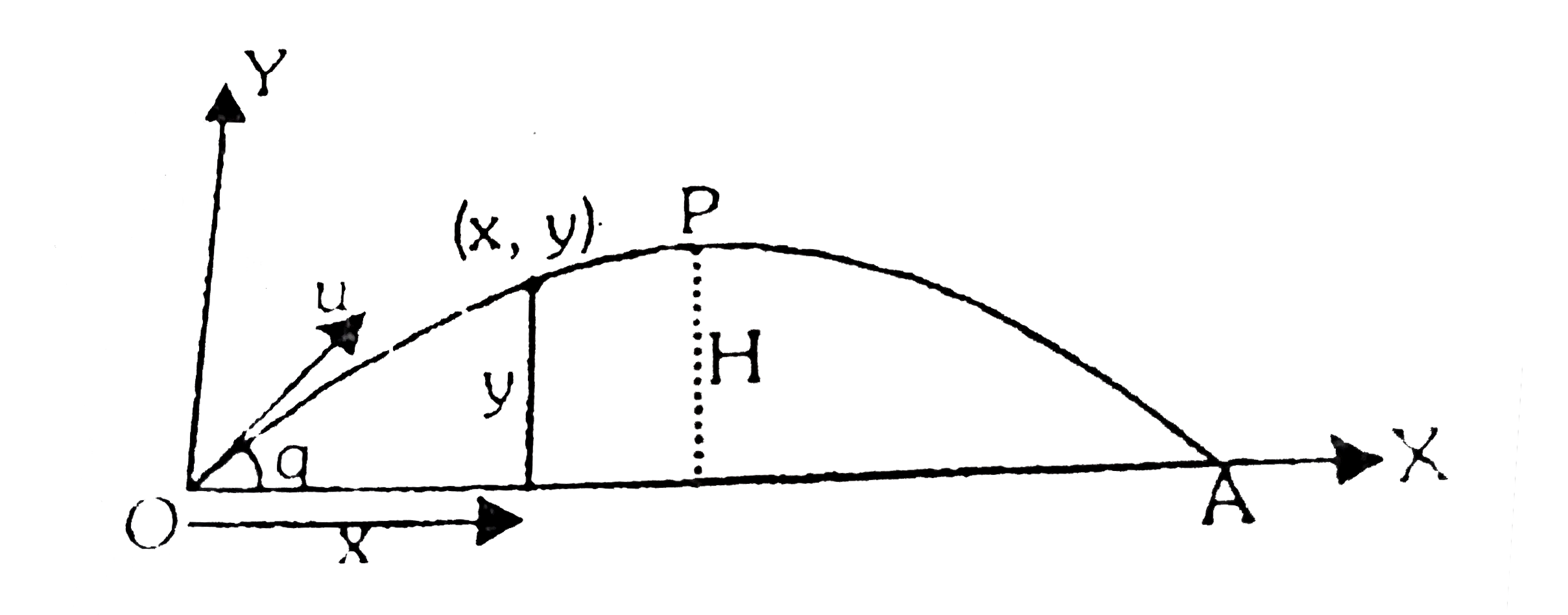
Range OA is :-
View Solution
