Trajectory of particle in a projectile motion is given as y=x−x280. Here, x and y are in meters. For this projectile motion, match the following with g=10m/s2.
Column-IColumn-II(A)Angle of projection (in degrees)(P)20(B)Angle of velocity with horizontal after 4s (in degrees)(Q)80(C)Maximum height (in meters)(R)45(D)Horizontal range (in meters)(S)30(T)60
The correct Answer is:(A)→(R);(B)→(R);(C)→(P);(D)→(Q)
To solve the problem, we will analyze the given trajectory equation of the projectile motion and extract the required information step by step.
Step 1: Identify the trajectory equation
The trajectory of the particle is given as:
y=x−x280
Step 2: Compare with the standard trajectory equation
The standard form of the trajectory for projectile motion is:
y=xtanθ−g2u2cos2θx2
where θ is the angle of projection, g is the acceleration due to gravity, and u is the initial velocity.
Step 3: Determine the angle of projection
From the given equation, we can see that:
- The coefficient of x is 1, which corresponds to xtanθ.
- The coefficient of x2 is −180, which corresponds to −g2u2cos2θ.
Since g=10m/s2, we can set up the following equations:
1. tanθ=1 (from the coefficient of x)
2. g2u2cos2θ=180
From tanθ=1, we have:
θ=45∘
Step 4: Calculate the horizontal range
The horizontal range R for projectile motion is given by:
R=u2sin2θg
Since θ=45∘, we have:
sin2θ=sin90∘=1
Thus,
R=u2g
From the comparison of coefficients, we know that:
R=80m
Step 5: Calculate the maximum height
The maximum height H for projectile motion is given by:
H=R4
Substituting R=80:
H=804=20m
Step 6: Calculate the angle of velocity with horizontal after 4 seconds
The time of flight T for projectile motion is given by:
T=2usinθg
Since θ=45∘:
T=2u⋅1√2g=u√25
Given that the total time of flight is 8s (since it takes 4 seconds to reach the maximum height), we can find u:
8=u√25⟹u=20√2
At t=4s, the angle of velocity with horizontal is still 45∘ because the projectile is symmetric in its motion.
Final Answers
- (A) Angle of projection: 45∘ (matches with R)
- (B) Angle of velocity with horizontal after 4s: 45∘ (matches with R)
- (C) Maximum height: 20m (matches with P)
- (D) Horizontal range: 80m (matches with S)
The trajectory of the particle is given as:
y=x−x280
The standard form of the trajectory for projectile motion is:
y=xtanθ−g2u2cos2θx2
where θ is the angle of projection, g is the acceleration due to gravity, and u is the initial velocity.
From the given equation, we can see that:
- The coefficient of x is 1, which corresponds to xtanθ.
- The coefficient of x2 is −180, which corresponds to −g2u2cos2θ.
1. tanθ=1 (from the coefficient of x)
2. g2u2cos2θ=180
θ=45∘
The horizontal range R for projectile motion is given by:
R=u2sin2θg
sin2θ=sin90∘=1
R=u2g
R=80m
The maximum height H for projectile motion is given by:
H=R4
H=804=20m
The time of flight T for projectile motion is given by:
T=2usinθg
T=2u⋅1√2g=u√25
8=u√25⟹u=20√2
- (A) Angle of projection: 45∘ (matches with R)
- (B) Angle of velocity with horizontal after 4s: 45∘ (matches with R)
- (C) Maximum height: 20m (matches with P)
- (D) Horizontal range: 80m (matches with S)
Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
15 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
Trajectory of particle in a projectile motion is given as y=x−x280. Here x and y are in metre. For this projectile motion match the following with g=10ms−2.

View SolutionIf y=x−x2 is the path of a projectile, then which of following is incorrect (g=10m/s2):
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Time of flight of the projectile is :-
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
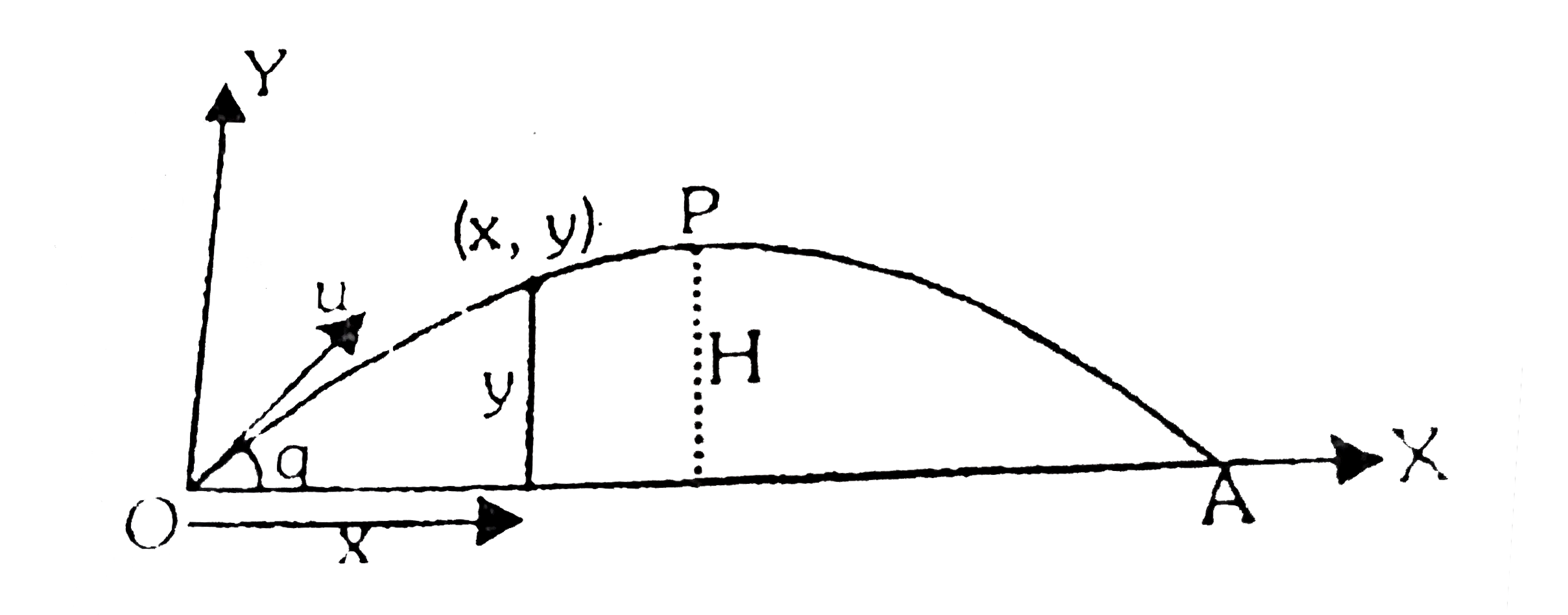
Range OA is :-
View SolutionEquation of trajectory of a projectile is given by y=−x2+10x where x and y are in meters and x is along horizontal and y is vericall y upward and particle is projeted from origin. Then : (g=10)m/s2
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Angle of projection θ is :-
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Maximum height H is :-
View SolutionFor ground to ground projectile motion equation of path is y=12x−3/4x2. Given that g=10ms−2. What is the range of the projectile ?
View SolutionThe horizontal and vertical displacements x and y of a projectile at a given time t are given by x=6tandy=8t−5t2 meter.The range of the projectile in metre is:
View SolutionEquation of trajector of ground to ground projectile is y=2x−9x2. Then the angle of projection with horizontal and speed of projection is : (g=10m/s2)
View Solution
