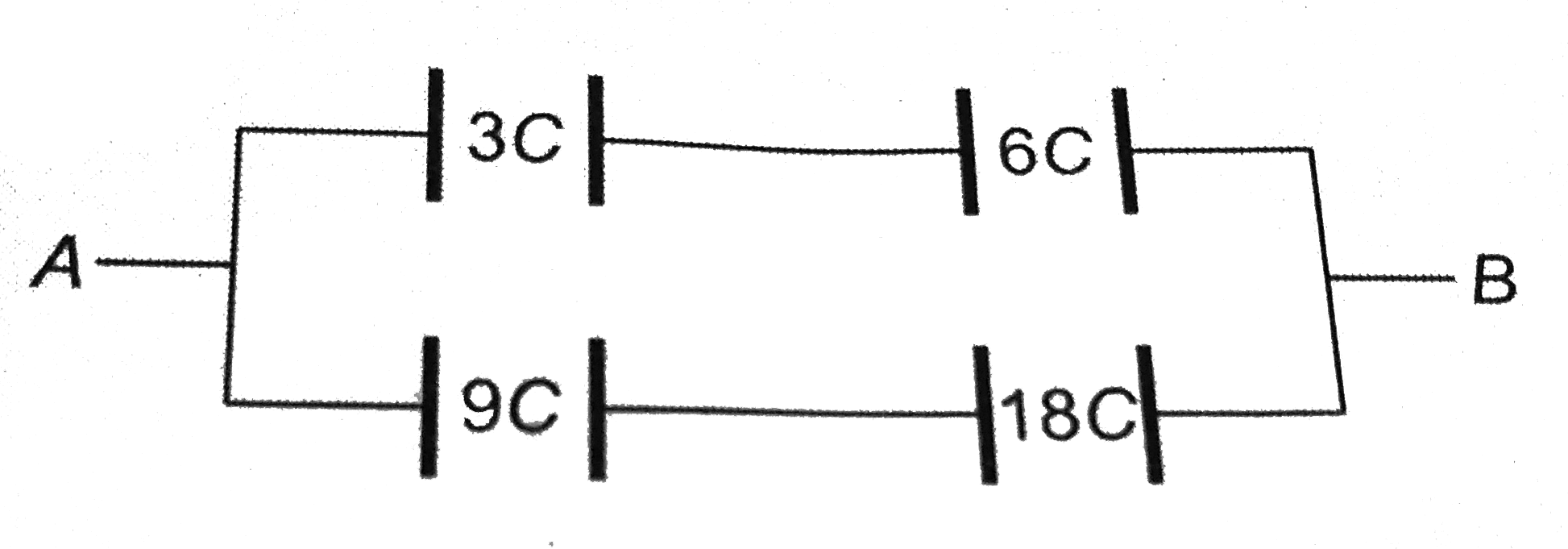
Twelve capacitors, each having a capacitance C, are connected to form a cube . Find the equivalent capacitance between the diagonally opposite corners such as A and B.

Video Solution
Text Solution
Consider the figure given below, let us assume a battery of potential difference V is connected at points A and G. The charge distribution is shown in the figure. We have to find equivalent capacitance between points A and G. All three capacitors connected to the point A are same so charge is equally divided among them. We have assumed total charge 6Q is supplied by the battery. It is first divided equally among three capacitors, hence 2Q each, and then from these branches this charge is equally divided between two capacitors hence Q each. Equivalent capacitance will
Ceq=6Q/V ...(i)
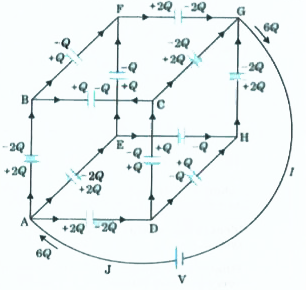
Let us apply Kirchhoff.s law for loop IJABFGI:
V−2Q/C−Q/C−2Q/C=0
⇒V=5Q/C
⇒Q=CV/5 ...(ii)
Substituting Q equation (ii) in equation (i) we get the following:
Ceq=6C/5
Alternate solution:
We can see that, due to same capacitance and charge in the capacitors of branches AD, AE and AB, electric potentials of points B, E and D are the same. Using the same logic electric potential of points C, H and F are also the same. We can put points of same potential at the same location and redraw the network as follows:
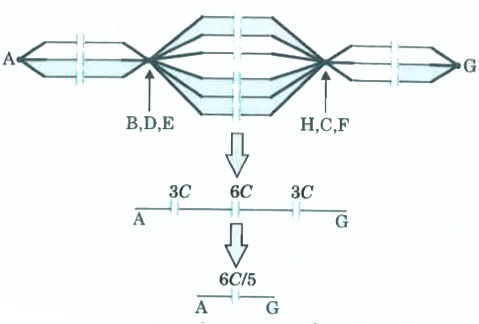
Hence, using above redrawn network we can find the answer as before by the series-parallel method.
|
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Textbook Exercise)
11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Additional Exercises)
23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Conceptual Questions
37 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
Knowledge Check
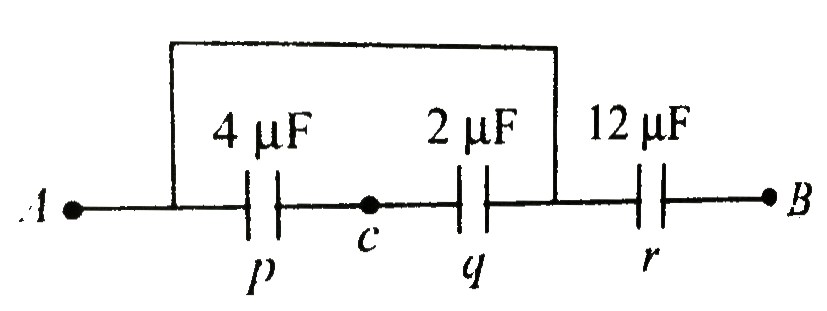
Find the equivalent capacitance between A and B
 A5μFB4μFC3μFD2μF
A5μFB4μFC3μFD2μFFind the equivalent capacitance between C and B.
 A6/5μFB5/6μFC4μFDnone of these
A6/5μFB5/6μFC4μFDnone of theseFind equivalent capacitance between A & B
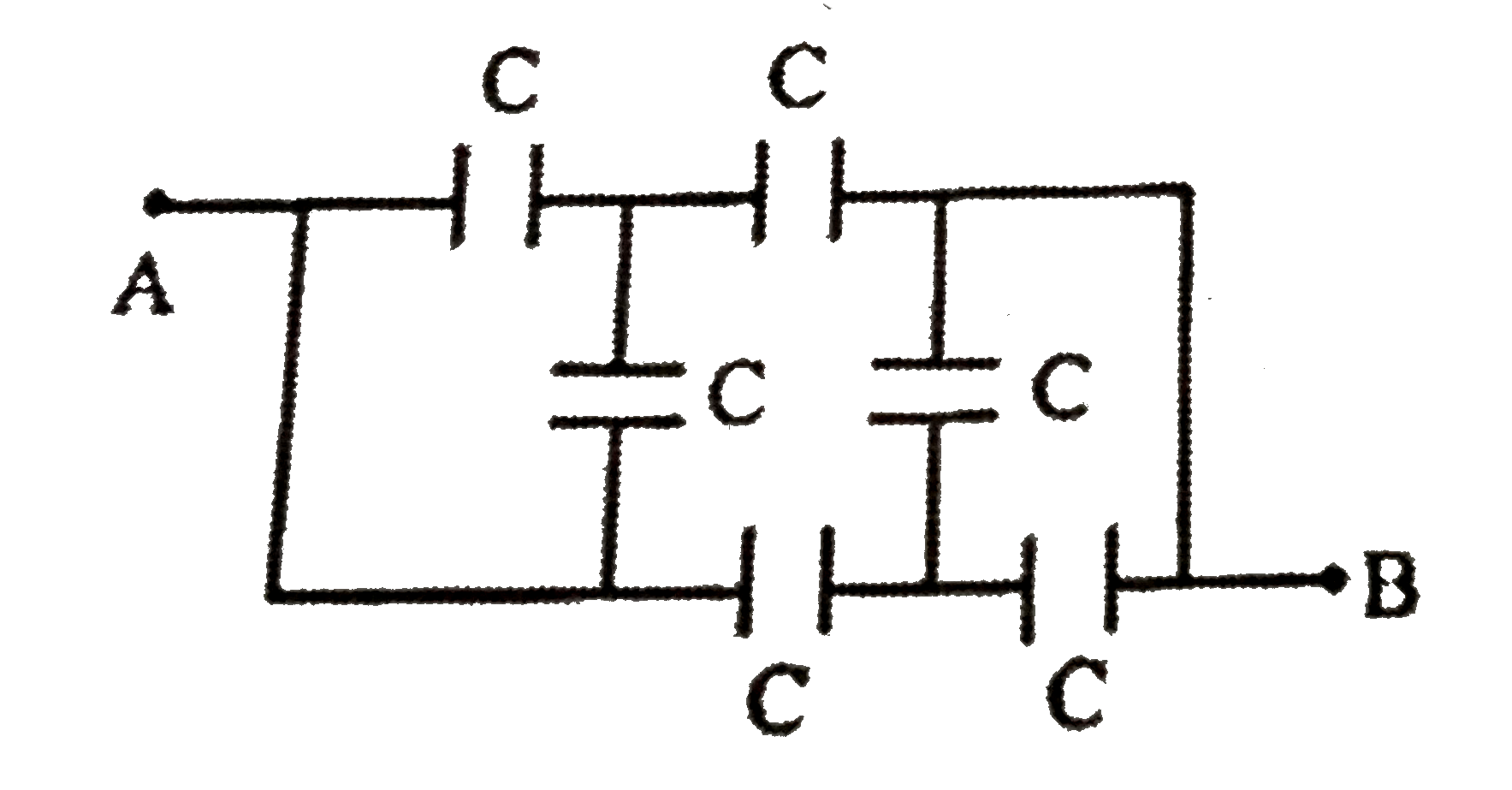 AC4B3G4C3G2D4G3
AC4B3G4C3G2D4G3
Find the equivalent capacitance between A and B.
View SolutionFind the equivalent capacitance between A and B.
View SolutionFind the equivalent capacitance between A and B.
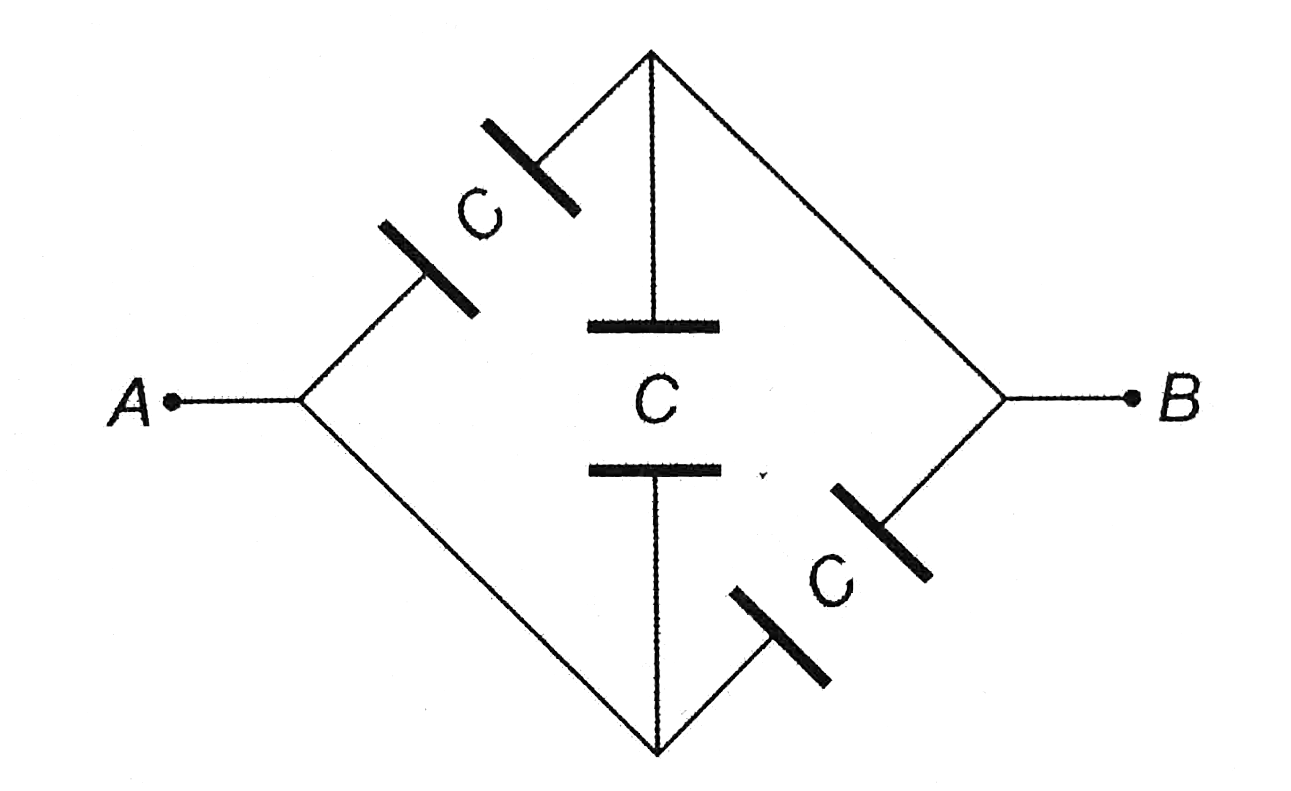
View SolutionFind the equivalent capacitance between A and B.
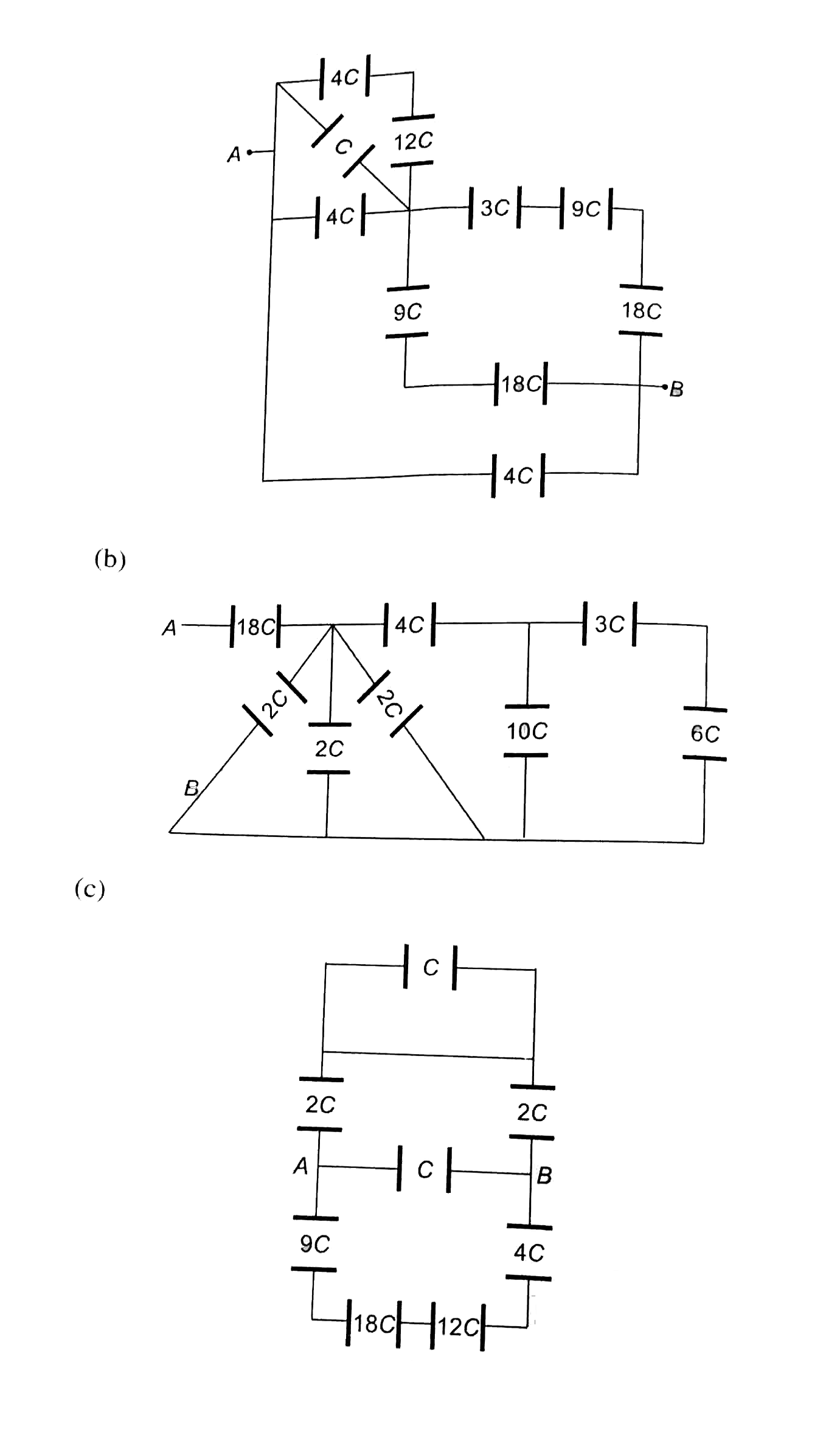
View SolutionFind the equivalent capacitance between A and B.
View Solution