Two balls of equal mass have a head on collision with speed 4ms−1 each travelling in opposite direction. If the coefficient's of resolution is 12, the speed of each ball after impact will be
1ms−1
2ms−1
3ms−1
data insufficient.
The correct Answer is:B
To solve the problem of the head-on collision of two balls of equal mass, we will follow these steps:
Step 1: Define the variables
Let the mass of each ball be m. The initial velocity of ball A, UA, is 4m/s (in the positive direction), and the initial velocity of ball B, UB, is −4m/s (in the negative direction).
Step 2: Write the equation for conservation of momentum
Since no external forces are acting on the system, the momentum before the collision is equal to the momentum after the collision. Thus, we have:
mUA+mUB=mVA+mVB
Substituting the values:
m(4)+m(−4)=mVA+mVB
This simplifies to:
0=mVA+mVB
Dividing through by m (since m≠0):
0=VA+VB⇒VA=−VB
Step 3: Use the coefficient of restitution
The coefficient of restitution e is defined as:
e=Relative velocity of separationRelative velocity of approach
Given e=12, we can express this as:
e=VB−VAUA−UB
Substituting the known values:
12=VB−VA4−(−4)=VB−VA8
This implies:
VB−VA=12×8=4
Step 4: Substitute VA in terms of VB
From Step 2, we know VA=−VB. Substituting this into the equation from Step 3:
VB−(−VB)=4⇒VB+VB=4⇒2VB=4
Thus, we find:
VB=2m/s
Step 5: Find VA
Using VA=−VB:
VA=−2m/s
Conclusion
The speed of each ball after impact is:
- Ball A: 2m/s in the negative direction
- Ball B: 2m/s in the positive direction
Thus, the speed of each ball after impact is 2m/s.
Final Answer
The speed of each ball after impact will be 2m/s.
---
Let the mass of each ball be m. The initial velocity of ball A, UA, is 4m/s (in the positive direction), and the initial velocity of ball B, UB, is −4m/s (in the negative direction).
Since no external forces are acting on the system, the momentum before the collision is equal to the momentum after the collision. Thus, we have:
mUA+mUB=mVA+mVB
Substituting the values:
m(4)+m(−4)=mVA+mVB
This simplifies to:
0=mVA+mVB
Dividing through by m (since m≠0):
0=VA+VB⇒VA=−VB
The coefficient of restitution e is defined as:
e=Relative velocity of separationRelative velocity of approach
Given e=12, we can express this as:
e=VB−VAUA−UB
Substituting the known values:
12=VB−VA4−(−4)=VB−VA8
This implies:
VB−VA=12×8=4
From Step 2, we know VA=−VB. Substituting this into the equation from Step 3:
VB−(−VB)=4⇒VB+VB=4⇒2VB=4
Thus, we find:
VB=2m/s
Using VA=−VB:
VA=−2m/s
The speed of each ball after impact is:
- Ball A: 2m/s in the negative direction
- Ball B: 2m/s in the positive direction
The speed of each ball after impact will be 2m/s.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns
9 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
Two balls of equal mass have a head-on collision with speed 6m/s. If the coefficient of restitution is 13, find the speed of each ball after impact in m/s
View SolutionTwo balls of equal masses m each undergo oblique collision. If colision is perfectly elastic, then angle between their velocities after collision is
View Solution
Knowledge Check
A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eBe−1e+1C1+e1−eDe+1e−1A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eB1+e1−eCe−1e+1De+1e−1
The first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
View Solution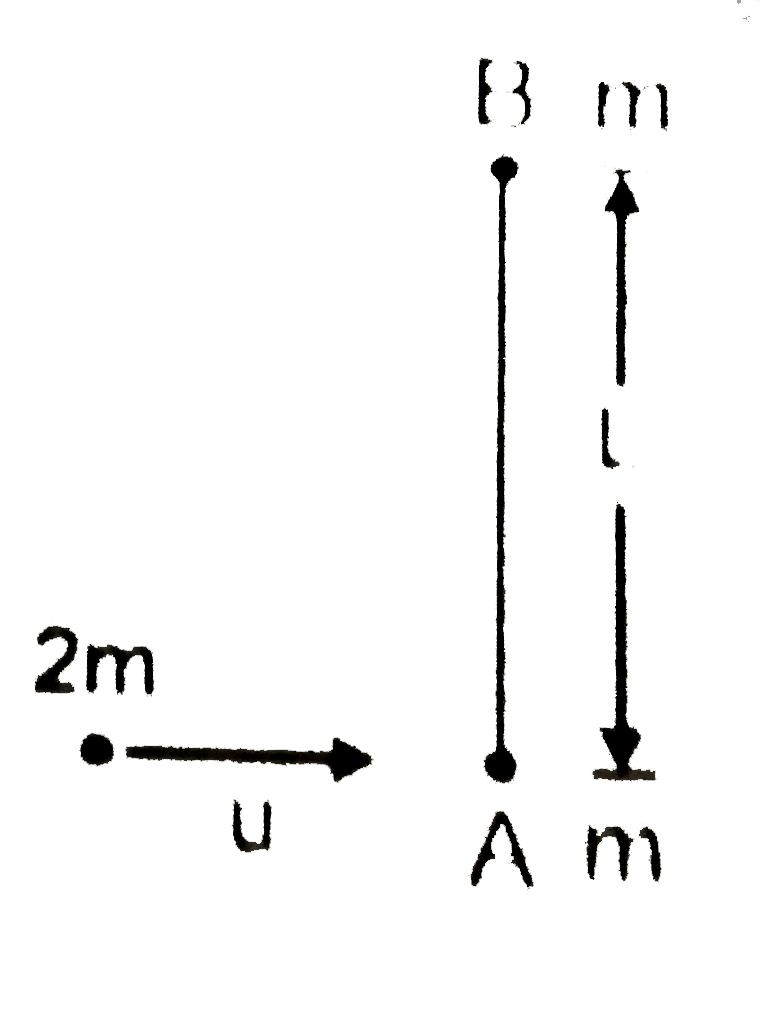
Two small balls A and B, each of mass m, are joined rigidly at the ends of a light rof of length L. they are placed on a frictionless horizontal surface another ball of mass 2 m moving with speed u towards one of the ball and perpendicular to the length of the rod on the horizontal frictionless surface as shown int he figure. if the coefficient of restitution is 1/2 then the angular speed of the rod after the collision will be
View SolutionA ball of mass m moving with velocity u collides head-on which the second ball of mass m at rest. If the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View SolutionA ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View SolutionA ball of mass 2kg moving with speed 5m/s collides directly with another ball of mass 3kg moving in the same direction with speed 4m/s. The coefficient of restitution is 2/3. Find the velocities of both ball after the collision.
View SolutionA ball P is moving with a certain velocity v, collides head-on with another ball Q of same mass at rest. The coefficient of restitution is 1/4, then ratio of velocity of P and Q just after the collision is
View Solution
