Two billiard balls are rolling on a flat table . One has the velocity component Vx=1ms−1,Vy=√3m−1 and the other has components Vx=2ms−1andVy=2ms−1 .If both the balls start moving from the same point , what is the angle between their paths ?
The correct Answer is:15∘
To find the angle between the paths of the two billiard balls, we will follow these steps:
Step 1: Identify the velocity components
The velocity components of the first billiard ball are:
- Vx1=1m/s
- Vy1=√3m/s
The velocity components of the second billiard ball are:
- Vx2=2m/s
- Vy2=2m/s
Step 2: Calculate the angles of the paths
To find the angle of each ball's path relative to the x-axis, we can use the tangent function:
- For the first ball:
tan(α1)=Vy1Vx1=√31=√3
Therefore,
α1=tan−1(√3)=60∘
- For the second ball:
tan(α2)=Vy2Vx2=22=1
Therefore,
α2=tan−1(1)=45∘
Step 3: Calculate the angle between the paths
The angle between the paths of the two balls can be found by subtracting the smaller angle from the larger angle:
Angle between paths=α1−α2=60∘−45∘=15∘
Final Answer
Thus, the angle between the paths of the two billiard balls is 15∘.
---
The velocity components of the first billiard ball are:
- Vx1=1m/s
- Vy1=√3m/s
- Vx2=2m/s
- Vy2=2m/s
To find the angle of each ball's path relative to the x-axis, we can use the tangent function:
- For the first ball:
tan(α1)=Vy1Vx1=√31=√3
Therefore,
α1=tan−1(√3)=60∘
tan(α2)=Vy2Vx2=22=1
Therefore,
α2=tan−1(1)=45∘
The angle between the paths of the two balls can be found by subtracting the smaller angle from the larger angle:
Angle between paths=α1−α2=60∘−45∘=15∘
Thus, the angle between the paths of the two billiard balls is 15∘.
Topper's Solved these Questions
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - FROM UNIT VECTORS COMPONENTS OF A VECTOR
6 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - FROM SCALAR PRODUCT AND VECTOR PRODUCT
20 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - VERY SHORT ANSWER QUESTIONS
10 Videos
- UNITSBOOK - ICSECHAPTER - UNITSEXERCISE - MODULE 3 (SELECTED PROBLEMS)
38 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - From Musical Sound
10 Videos
Similar Questions
Two balls are rolling on a flat smooth table. One ball has velocity components √3ˆj and ˆi while the other has components 2ˆi and 2ˆj. If both start moving simultaneously from the same point, the angle between their paths is-
View SolutionOne of the rectangular components of a velocity of 20 ms−1 is 10 ms−1. Find the other component.
View Solution
Knowledge Check
Two particles of equal mass have velocities v1=2ims−1 and v2=2jms−1 First particle has an acceleration a=(3i+3j)ms−2 while the acceleration of the other particle is zero. The centre of mass of the two particles moves in a path of
Aa.straight lineBb.parabolaCc.circleDd.ellipse
A particle is moving in the x-y plane. At certain instant of time, the components of its velocity and acceleration are as follows: vx=3ms−1,vy=4ms−1,ax=2ms−2anday=1ms−2. The rate of change of speed at this moment is
View SolutionThe collision of two balls of equal mass takes place at the origin of coordinates. Before collision, the components of velocities are (vx=50cm−1 , vy=0) and (vx=−40cm−1 and vy=30cms−1. The first ball comes to rest after collision. The velocity (components vx and vy respectively) of the second ball are
View SolutionThe three block shown in fig. move with constant velocities. Find the velocity of blocks A and B. given VP2=10ms−1⏐↓,VC=2ms−1↑⏐.

View SolutionTwo particles are moving with velocities v1andv2 . Their relative velocity is the maximum, when the angle between their velocities is
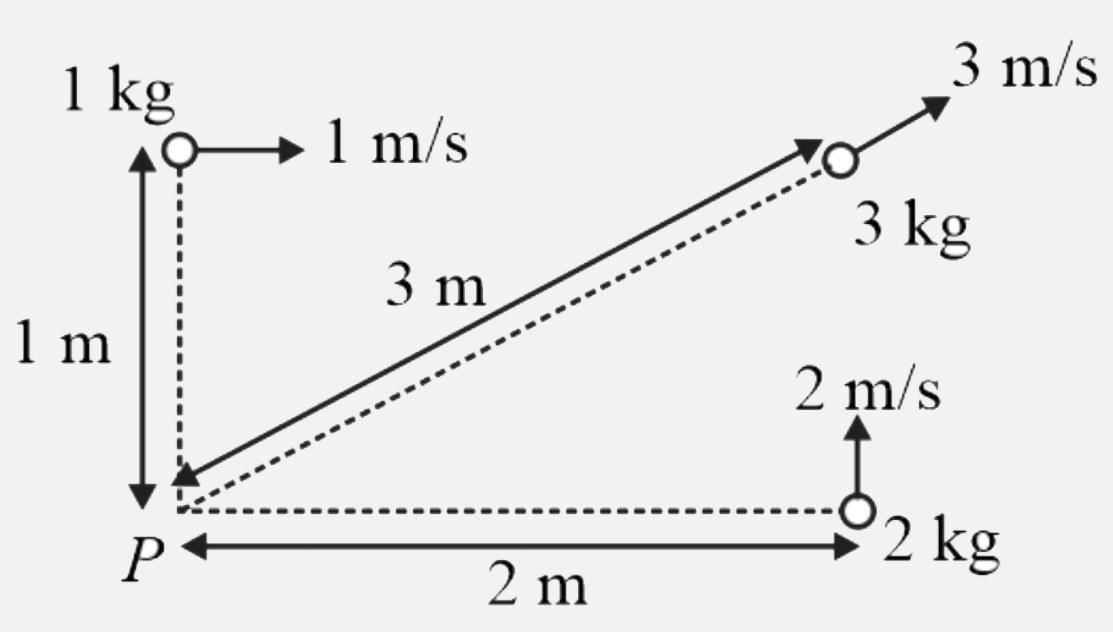
View SolutionThree small balls of masses 1kg, 2kg and 3kg are moving in a plane and their velocities are 1ms−1,2ms−2and3ms−1 respectively as shown . The total angular momentum of the system of three balls about point P at the given instant of time is
View SolutionTwo particles of equal masses have velocities →v1=4ˆims−1 and →v2=4ˆjms−1. First particle has an acceleration →a1=(5ˆi+5ˆj)ms−2, while the acceleration of the other particle is zero. The centre of mass of the two particles moves in a path of
View SolutionTwo spheres of masses 4 kg and 8 kg are moving with velocities 2ms−1and3ms−1 away from each other along the same line. The velocity of centre of mass is
View Solution
