Two block of masses and are connected by a chord passing around a frictionless pulley which is attached to a rotating frame , which rotates about a vertical axis with an angular velocity If the coefficient of friction between the two masses and the surface are and respectively determine the value of at which the block starts sliding radially

The correct Answer is:
Evidently the larger block of mass experience move centrifugal force redially outwards compared to the block of smaller block m
figure shown than FBD
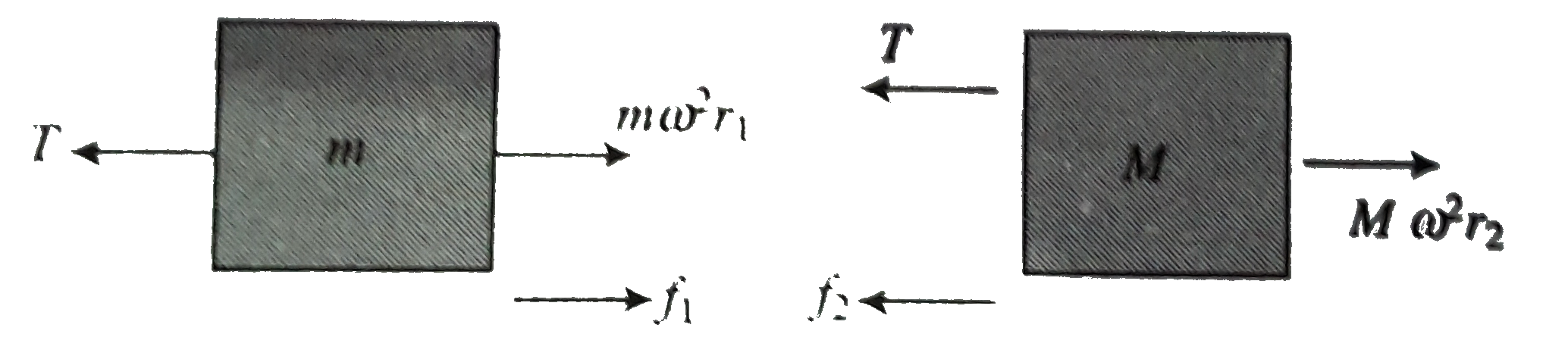
Owing to the large force exerienced by block of mass is tends in fly off redally
In the situation of limiting equilibrium we have
(where and are frictional forces for the two block and the surface)
...(i)
The above two equations get reduced to
...(ii)
Subtracting Eq (i) from Eq(ii),
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct
87 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.3
27 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Two blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
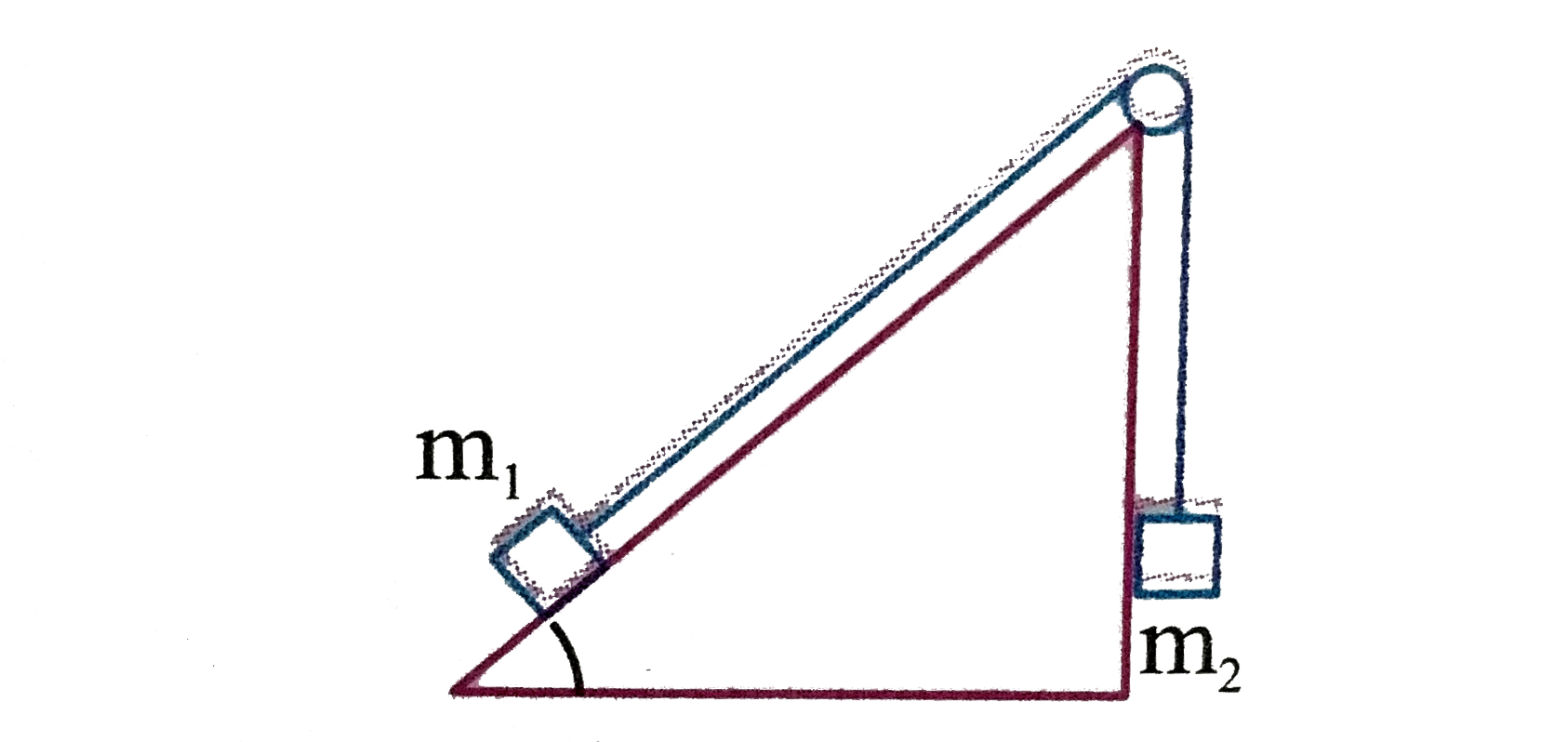
View SolutionTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
View SolutionTwo blocks of equal masses are connected by an ideal string passing over an ideal pulley as shown in the figure
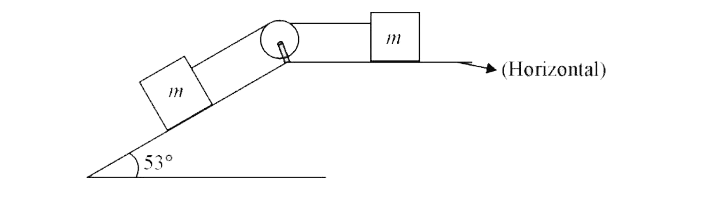
All the surfaces in contact with blocks are rough having coefficient of kinetic friction μ between them. If the blocks slide with constant velocity, find the value of μ
View SolutionA solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
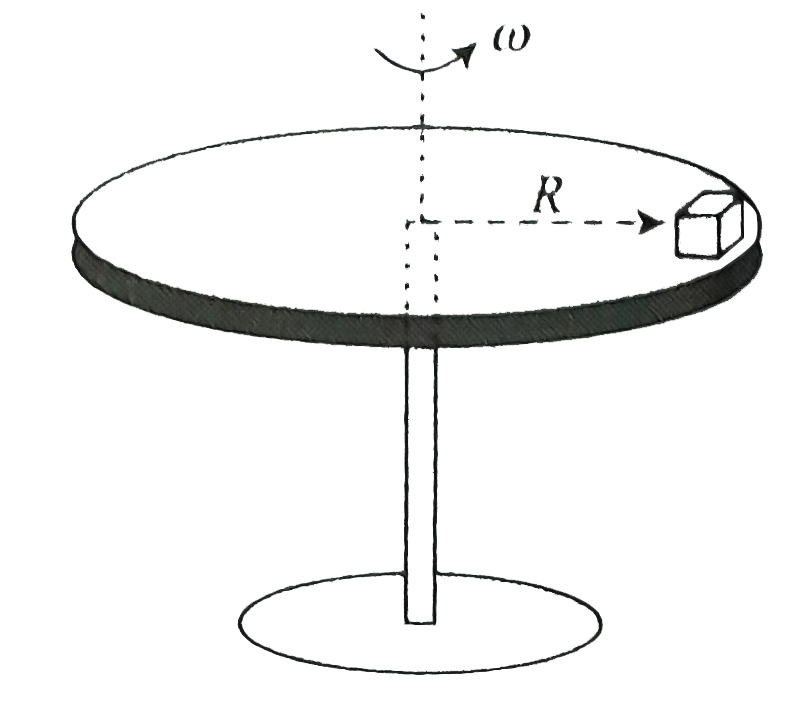
View SolutionA block of mass m is kept on the edge of a horizontal turn table of radius R which is rotating with constant angular verticle ω (along with the block ) about its axis . If coefficient of friction is μ, find the friction force between block and table.
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly
View SolutionA block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is

View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionThere are two blocks of masses m1 and m2,m1 is placed on m2 on a table which is rotating with an angular velocity ω about the vertical axis . The coefficent of friction between the block is μ1 and between m2 and table is μ2(μ1<μ2) if block are placed at distance R from the axis of ratation , for relative sliding between the surface in contact , find the
a. friction force at the contacting surface
b. maximum angular speed ω

View Solution
