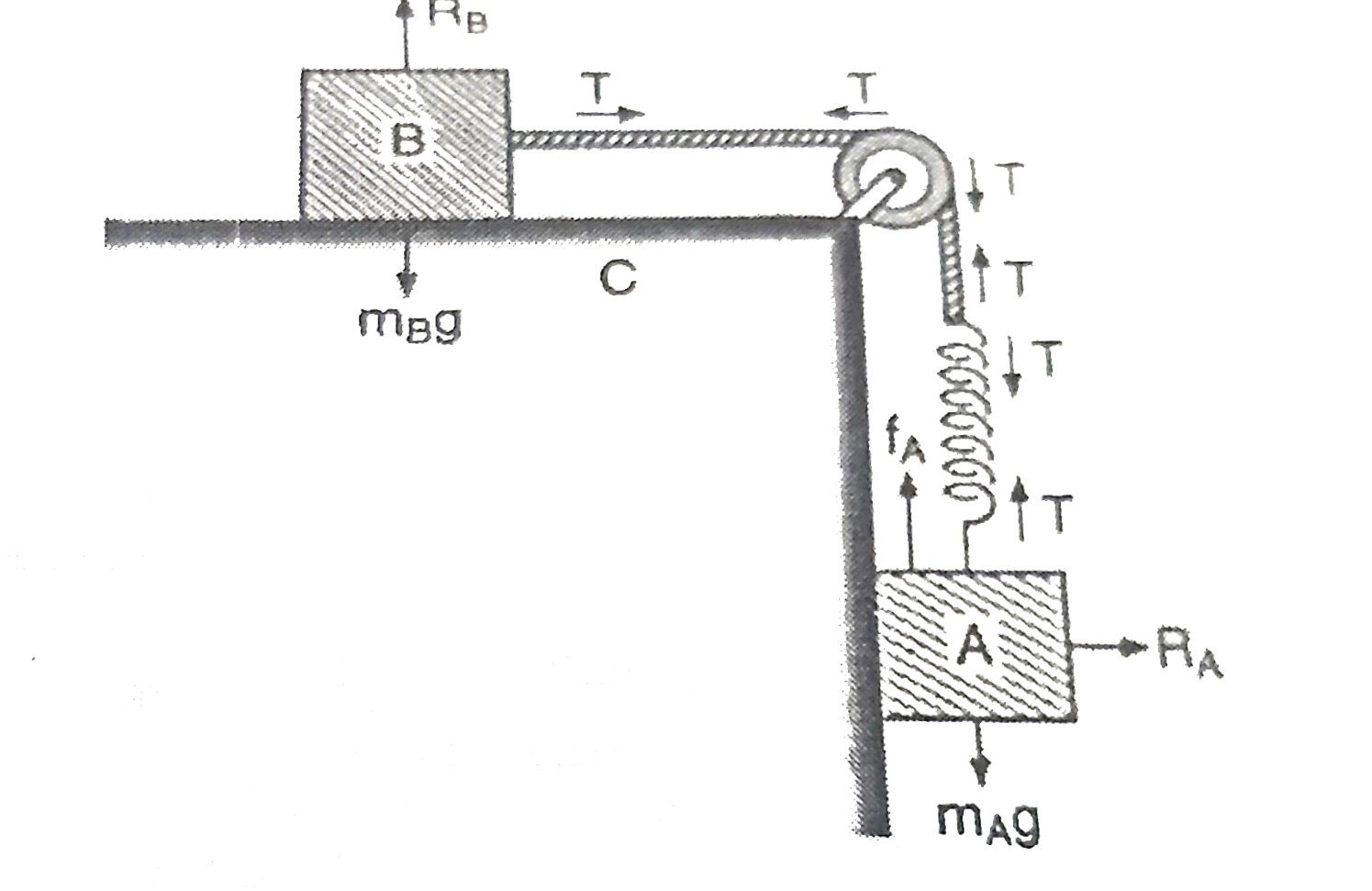
Two blocks A and B are connected to each other by a string and a spring, the string passes over a frictionless pulley as shown in Block B slides over the horizontal surface of a stationary block C and the block. A slides along the vertical side of C, both with same uniform speed. The coefficient of friction between the surface of the blocks is 0.2 Force constant of the spring is 1960 N/m if the mass of block A is 2 kg calculate the mass of the block B and the energy stored in the spring.
In this problem:
(1) As masses A and B are moving with constant velocity this is a problem of dynamic equilibium i.e., forces acting on mass A (or B) balance each other.
(2)As string and spring are weithless and no mass is involved between them, Tstring=Tspring=T
(3) Force of friction on block B, fB=μRB=μmBg (as RB=mBg) while on block A, fA=μRA=0 (as RA=mAgcos90∘=0)
In the light of above for horizontal equilibrium of B,
T=fB=μmBg ....(i)
While for vertical equilibrium of A,
T=mAg ....(ii)
So, from Eqns (i) and (ii)
μmBg=mAg
mB=(2/0.2)=10kg
Now, as for spring T=ky in the light of Eqn. (ii) becomes
ky=mAgi.e.,y=(2×9.8)/1960=10−2m
So, the enegy stored in the spring
U=(1/2)ky2=(1/2)×1960×(10−2)2=0.098J
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem for practice
30 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Objective Questions
134 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
Two blocks A and B are connected to each other by a string and a spring , the string passes over a frictionless pulley as shown in the figure. Block B slides over the horizontal top surface of a stationary block C and the block A slides along the vertical side of C, both with the same uniform speed. The coefficient of friction between the surface and blocks is 0.5K=2000N/m. If mass of A is 2kg calculate mass of B.
 .
.
View SolutionTwo blocksA andB are connected to each other by a string and a spring , the spring pases and a frictionlesss pulley as down over in the figure . Block B sides over the horizental top surface of a strionry block C both with the verical side of C , both with the same conform speed
The coefficient of friction between the surface the of block is 0.2 force constant of the spring is 1960 newtons , if mass of block A is 2 kg , celculate the mass of block F and B and the energy stored is the spring
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Two blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
 A4m/s2B2m/s2CzeroD6m/s2
A4m/s2B2m/s2CzeroD6m/s2Two blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is
 A50N up the planeB50N down the planeC100N up the planeD100N down the plane
A50N up the planeB50N down the planeC100N up the planeD100N down the plane
If the two blocks moves with a constant uniform speed then find coefficient
of fricition between the surface of the block B and the table. The spring is massless and the pulley is fricitionless.
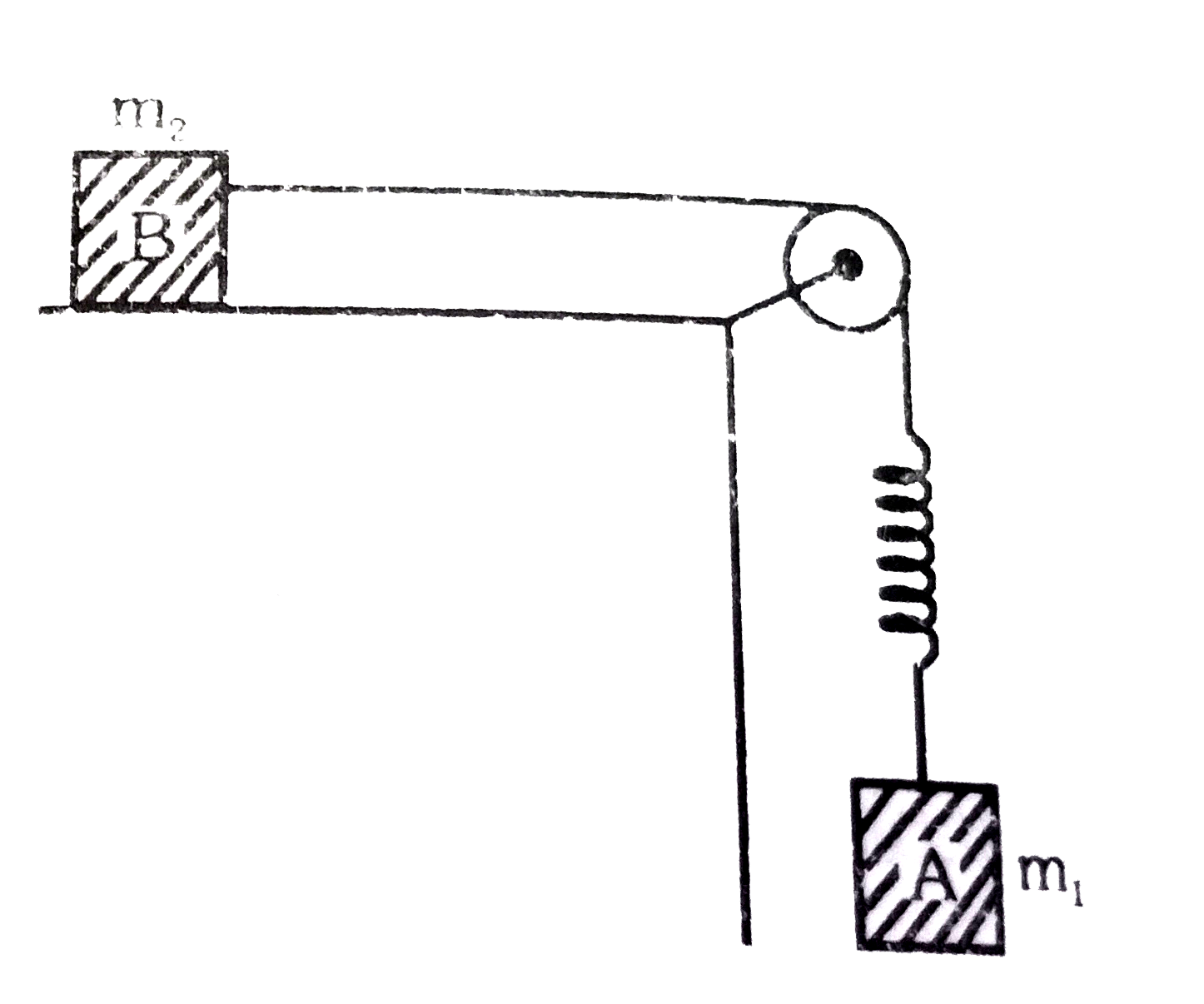
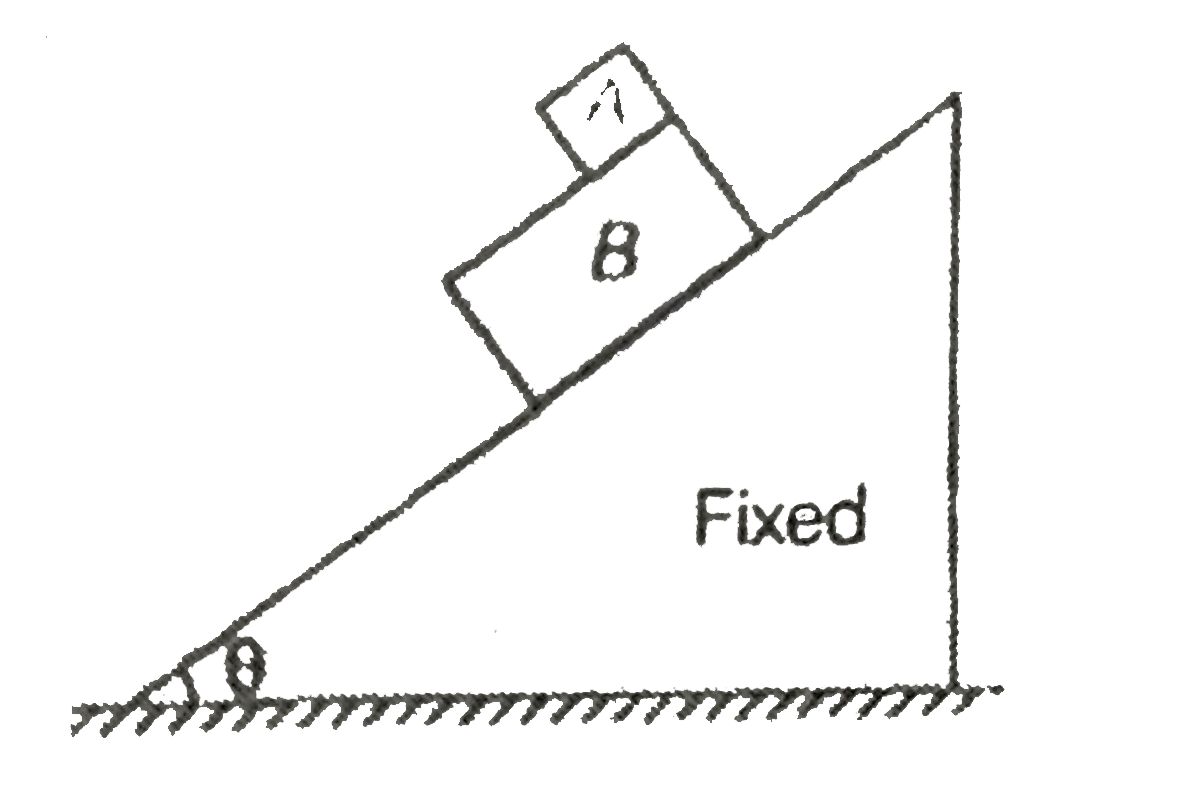
View SolutionA block A slides over an another block B which is placed over a smooth inclined plane as shown in figure . The coefficient of friction between the two blocks A and B is μ . Mass of block B is two times the mass of block A . The acceleration of the centre of mass of two blocks is
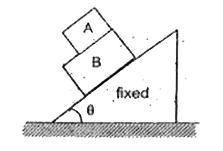
View SolutionA block A slides over another block B which is placed over a smooth inclined plane. The coefficient of friction between the two blocks. A and B is μ. Mass of block B is two times the mass of block A. The acceleration of the centre of mass of two blocks is
View SolutionBlock A of mass M in the system shown in the figure slides down the incline at a constant speed. The coefficient of friction between block A and the surface is 1 3 3 . The mass of block B is-

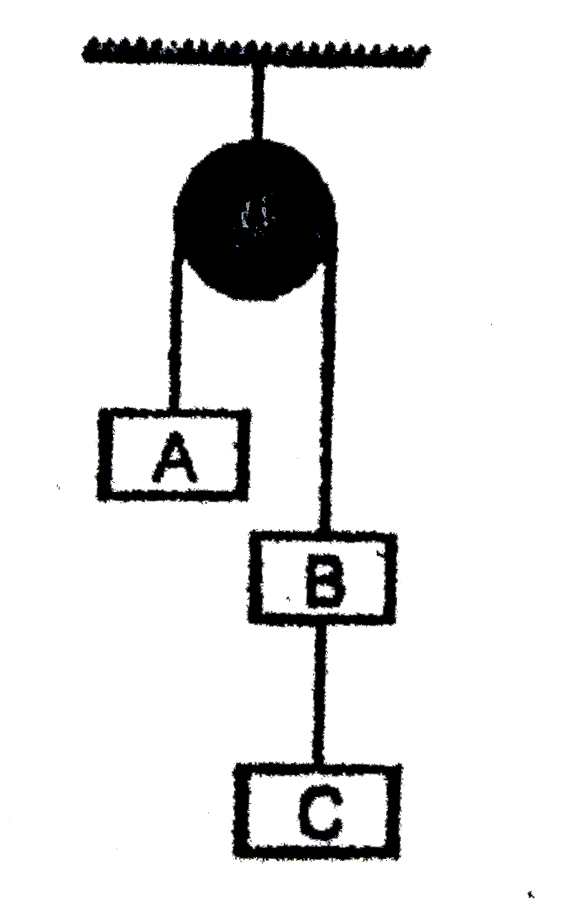
View SolutionThree blocks A,B and C of mass 10 kg each are hanging on a string passing over a fixed frictionless pulley as shown in figure. The tension in the string connecting blocks B and C is (g=10m/s2)
View Solution
