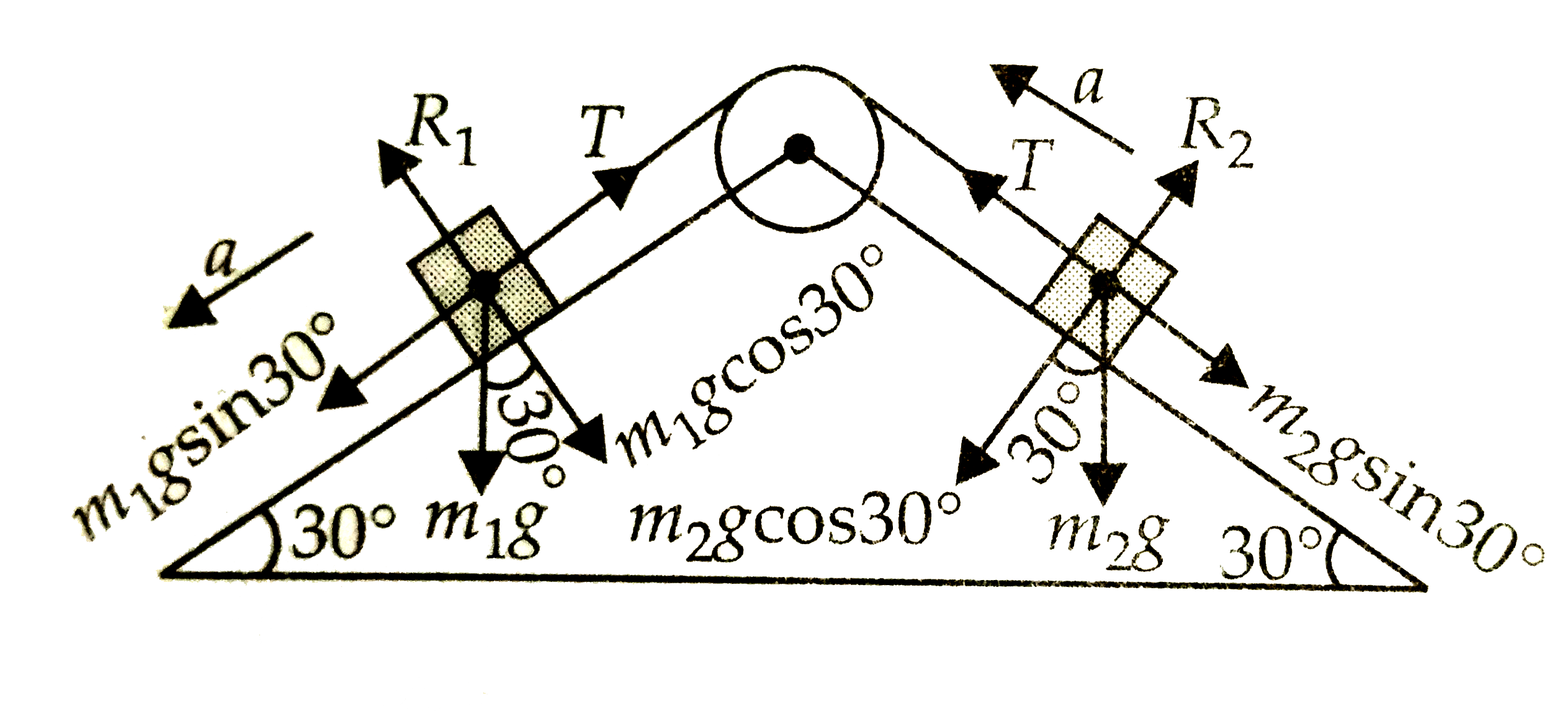
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.

0.7ms−2
0.8ms−2
0.6ms−2
0.5ms−2
The correct Answer is:A
Hence, m1=40g
m2=30kg,θ=30∘
Let T be the tension in the string and a be the acceleration of the system. Their equations of motion are m1sin30∘−T=m1a…(i)
T−mgsin30∘=m2a…(ii)
Adding (i) and (ii), we get
(m1+m2)a=(m1−m2)gsin30∘
Substituting the given values, we get
(40+30)a=(40−30)×9.8×12=49
a=4970=0.7ms−2
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Higher Order Thinking Skills
8 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - NCERT Exemplar
9 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Circular Motion
14 Videos
- KINETIC THEORYBOOK - NCERT FINGERTIPSCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
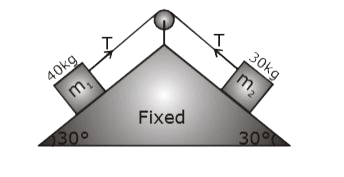
Two masses 40kg and 30 kg connected by a massless string passing over a frictionless light pulley as shown in the figure. The tension ( almost ) in the string will be : ( All surfaces are frictionless)
View SolutionTwo blocks A and B of respective masses 6 kg and 4 kg are connected with a string passing over a light friction less pulley as shown in the figure . The coefficient of friction between the block A and horizontal surface is 0.4 . Then the minimum mass of block C which should be placed over A to prevent it from moving is :
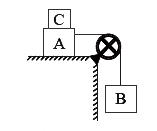
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A188 NB2=368 NC288 ND168 N
A188 NB2=368 NC288 ND168 NTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Two blocks of masses m and 2m are connected by a light string passing over a frictionless pulley. As shown in the figure, the mass m is placed on a smooth inclined plane of inclination 30° and 2m hangs vertically. If the system is released, the blocks move with an acceleration equal to :
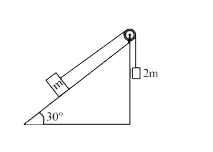 Ag/4Bg/3Cg/2Dg
Ag/4Bg/3Cg/2Dg
Two blocks of mass 10kg and 2kg respectively are connected by an ideal string passing over a fixed smooth pulley as shown in figure. A monkey of mass 8kg started climbing the string with a constant acceleration of 2m/s2 with respect to string at t=0 . Initially the system is in equilibrium and monkey is at a distance 2.4 from the pulley. Find the time taken by monkey to reach the pulley in sec.
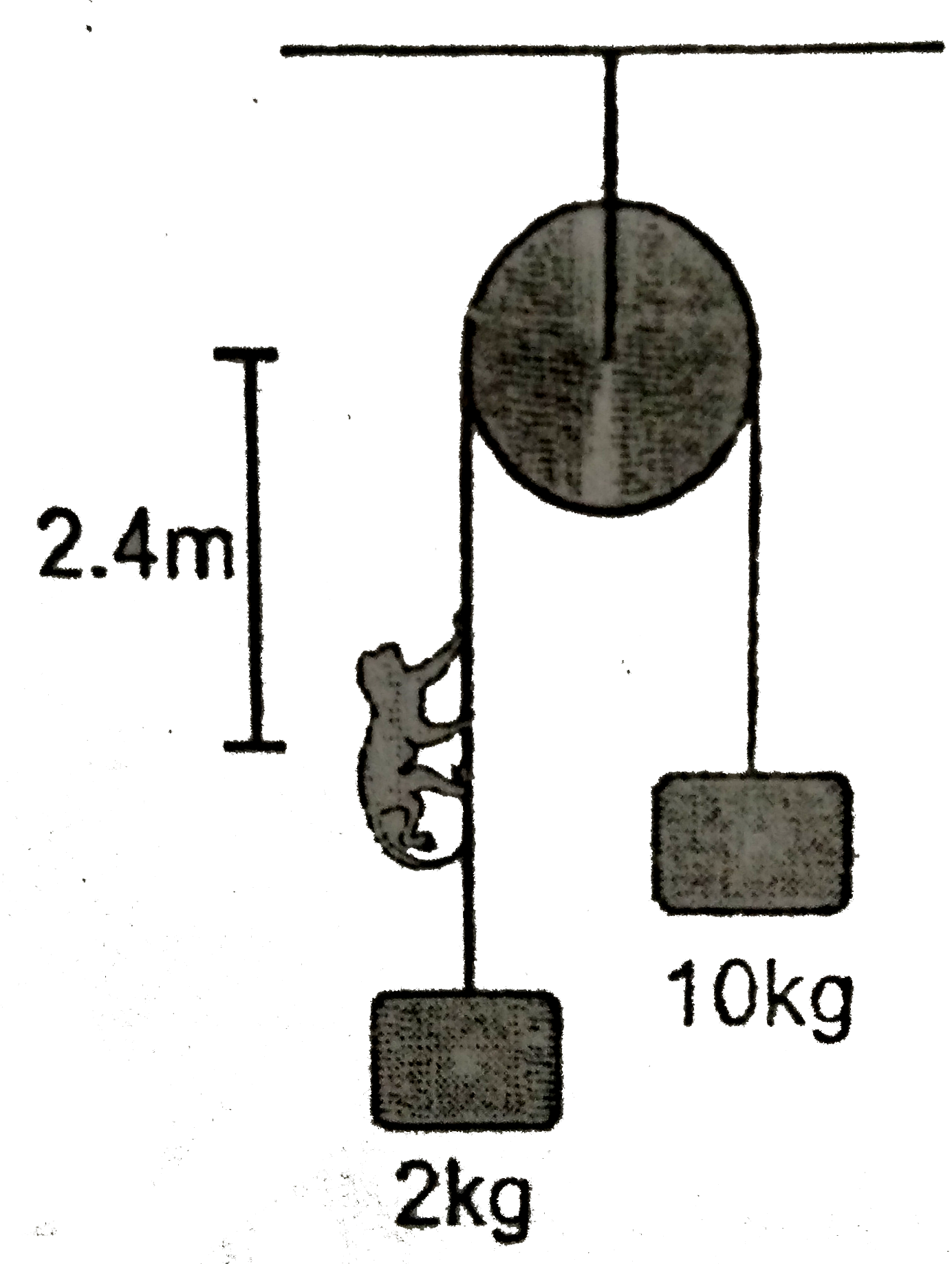
View SolutionTwo blocks of masses 50 kg and 30 kg connected by a massless string pass over a light frictionless pulley and rest on two smooth planes inclined at angles 30∘ and 60∘ resp . With horizontal .Determine the accelertion in the two blocks and tension in the string g=10m/s2 .
View SolutionTwo masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
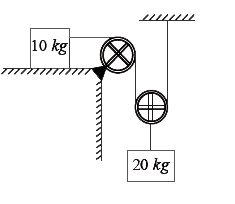
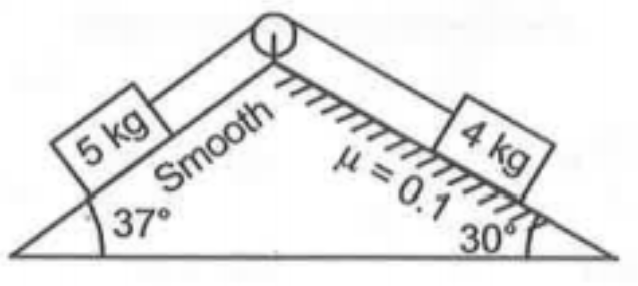
View SolutionTwo blocks of masses 5 kg and 4 kg are connected with ideal string which is passing over an ideal pulley as shown in figure. If the system is released from rest then the magnitude of acceleration of the blocks will be (Take g=10ms−2and√3=1.7)
View SolutionTwo blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is

View Solution
