Two capacitors of capacitances and are connected in series with a 6.00V bettery . Find (a )the potential difference across each capacitor and (b) the energy stored in each capacitor .
To solve the problem step by step, we will first find the equivalent capacitance of the capacitors in series, then calculate the charge, the potential difference across each capacitor, and finally the energy stored in each capacitor.
Step 1: Calculate the Equivalent Capacitance
For capacitors in series, the formula for the equivalent capacitance C is given by:
1C=1C1+1C2
Where:
- C1=20.0pF
- C2=50.0pF
Substituting the values:
1C=120.0+150.0
Calculating the right-hand side:
1C=5100+2100=7100
Thus,
C=1007≈14.286pF
Step 2: Calculate the Charge Stored in the Capacitors
The charge Q on the capacitors can be calculated using the formula:
Q=C⋅V
Where:
- V=6.00V (the voltage of the battery)
Substituting the values:
Q=14.286pF⋅6.00V=85.716pC
Step 3: Calculate the Potential Difference Across Each Capacitor
The potential difference across each capacitor can be calculated using the formula:
V1=QC1andV2=QC2
For Capacitor 1:
V1=QC1=85.716pC20.0pF=4.286V
For Capacitor 2:
V2=QC2=85.716pC50.0pF=1.714V
Step 4: Calculate the Energy Stored in Each Capacitor
The energy E stored in each capacitor can be calculated using the formula:
E=12CV2
For Capacitor 1:
E1=12C1V21=12⋅20.0pF⋅(4.286V)2
Calculating:
E1=12⋅20.0⋅18.387≈184.04pJ
For Capacitor 2:
E2=12C2V22=12⋅50.0pF⋅(1.714V)2
Calculating:
E2=12⋅50.0⋅2.938≈73.469pJ
Final Answers:
(a) The potential difference across the capacitors are:
- V1≈4.286V
- V2≈1.714V
(b) The energy stored in each capacitor are:
- E1≈184.04pJ
- E2≈73.469pJ
For capacitors in series, the formula for the equivalent capacitance C is given by:
- C1=20.0pF
- C2=50.0pF
The charge Q on the capacitors can be calculated using the formula:
- V=6.00V (the voltage of the battery)
The potential difference across each capacitor can be calculated using the formula:
V1=QC1=85.716pC20.0pF=4.286V
V2=QC2=85.716pC50.0pF=1.714V
The energy E stored in each capacitor can be calculated using the formula:
E1=12C1V21=12⋅20.0pF⋅(4.286V)2
E2=12C2V22=12⋅50.0pF⋅(1.714V)2
(a) The potential difference across the capacitors are:
- V1≈4.286V
- V2≈1.714V
- E1≈184.04pJ
- E2≈73.469pJ
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer7videos
CAPACITORS
- BOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 26videos
CAPACITORS
- BOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer10videos
BOHR'S MODEL AND PHYSICS OF THE ATOM
- BOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer6videos
DISPERSION AND SPECTRA
Similar Questions
If A is connerted with D and B is connected with C find the potential difference a across each capacitor and the final charge in each capacitor.
View SolutionTwo capacitor of capacitance 4.0μFand 6.0muF' are connected in series with a battery of 20 V . Find the energy supplied by the battery .
View SolutionFind charge on each capacitor and potential difference across each capacitor .
 View Solution
View SolutionThree capacitors each of capacitance 9 pF are connected in series. What is the total capacitance of the combination ?
View SolutionThree capacitors having capacitances of 8.4μF,8.4μF and 4.2μF are connected in series across a 36 potential difference.
(a) What is the charge on 4.2μF capacitor?
(b) What is the total energy stored in all three capacitors?
(c) The capacitors are disconnected from the potential difference without allowing them to discharge. They are then reconnected in parallel with each other, with the positively charged plates connected together. What is the voltage across each capacitor in the parallel combination?
(d) What is the total energy now stored in the capacitors?View SolutionThe capacitor of capacitance 4μF and 6μF are connected in series. A potential difference of 500 volts applied to the outer plates of the two capacitor system. Then the charge on each capacitor is numerically
View SolutionA capacitor of capacitance C is charged to a potential differece V0. The terminals of the charged capacitor are then connected to those of an uncharged capacitor of capacitance C/2.
a. Compute the original charge of the system.
b. Find the final potential differce across each capacitor.
c. Find the final energy of the system.
d. Calculate the decrease in energy when the capacitors are connected.
e. Where did the ''lost'' energy go?View SolutionThree capacitors 3μF,6μF and 6μF are connected in series to source of 120 V. The potential difference in volt, across the 3μF capacitor will be
View SolutionThree capacitors of capacitances 3μF, 6μF, and 4μF are connected as shown across a battery of emf 6V.
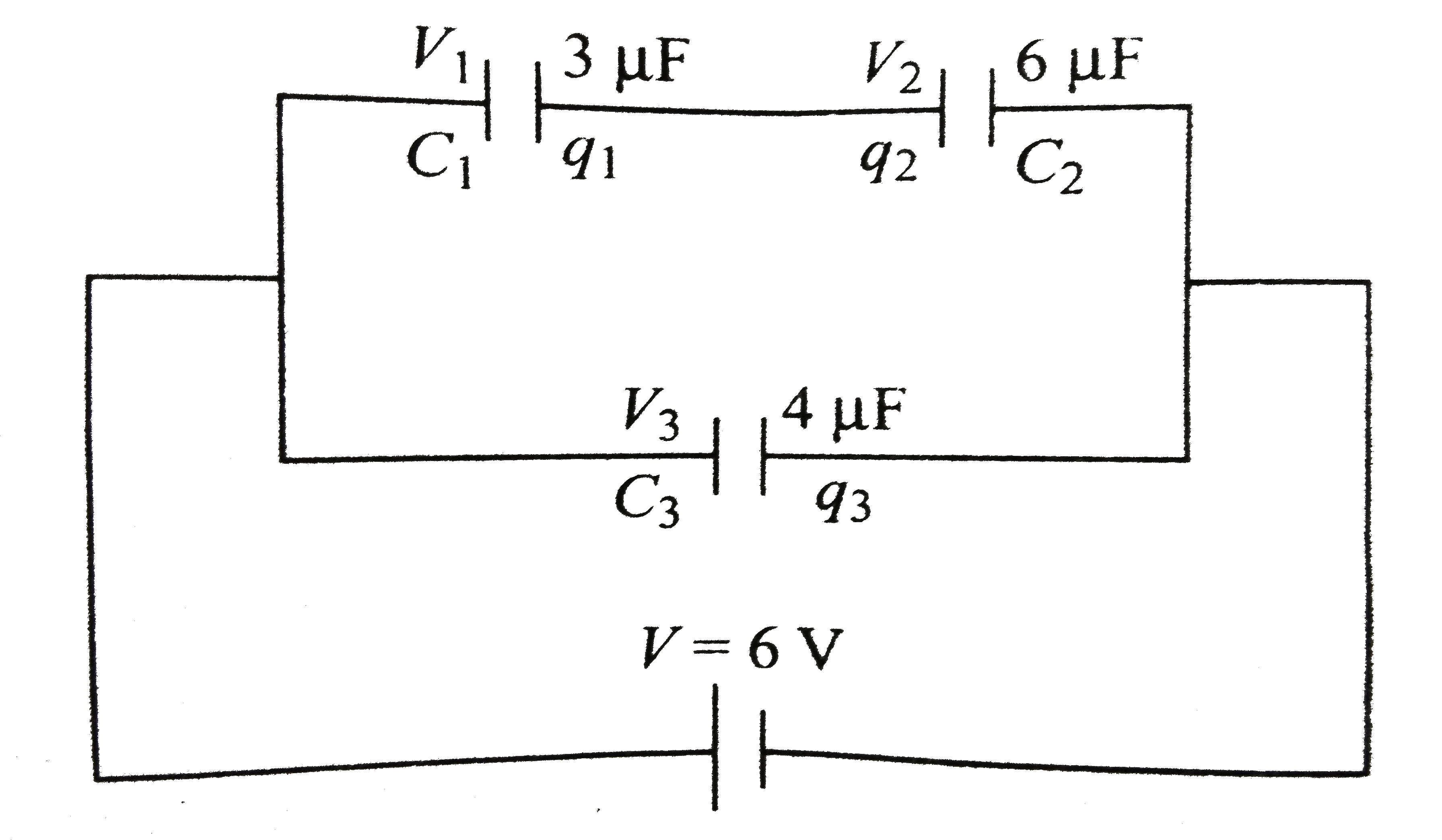 .
.
i. Find the equivalent capacitance,
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in the system of capacitors and total energy stored in the system of capacitor.View SolutionThree capcitors of capacitances 4μF,
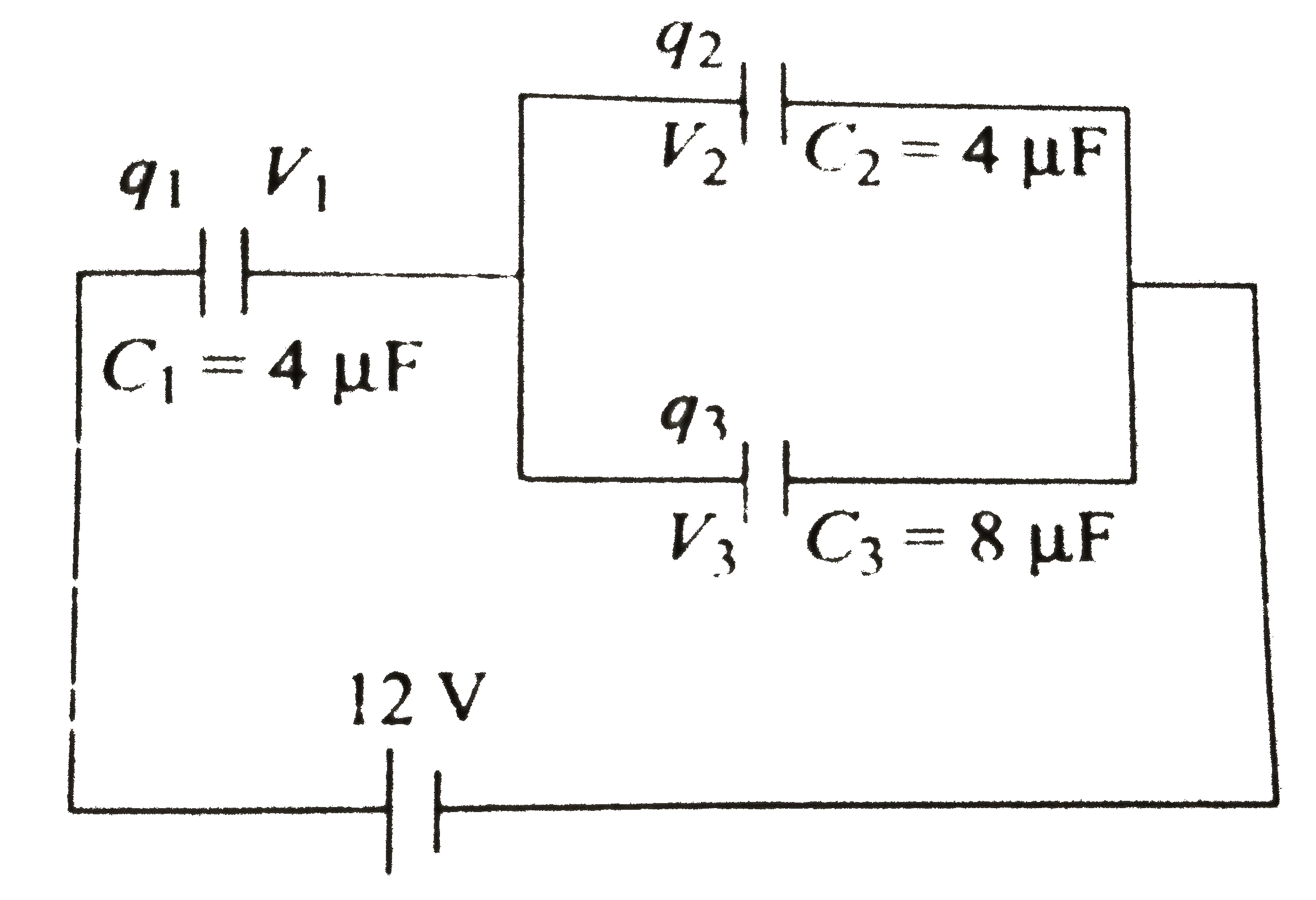 .
.
4μF, and 8μF, are connected as show across a battery of emf 12V.
i. Find the equivalent capacitane.
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in each capacitor and the total energy stored in the system of capacitors.View Solution
