Two charges q1andq2 are placed at (0,0,d) and (0,0,-d) respectively. Find locus of points where the potential is zero.
In fig, we have shown two charges q1(0,0,d)andq2(0,0,d). For potential to be zero at (x,y,z) we should have q14π∈0√x2+y2+(z−d)2+q24π∈0√x2+y2+(z+d2)=0
q1√x2+y2+(z−d2)=−q2√x2+y2+(z+d2) ...(i)
Clearly, total potential can be zero when q1,q2 have opposite signs.
Sqaring both sides of (i), we get q21[x2+y2+(z+d)2]=q22[x2+y2+(z−d)2]
on simlifying we get x2+y2+z2+[(q1/q2)2+1(q1/q2)2−1](2zd)+d2=0.
This is the equaction of a sphere will center at [0,0,−2d(q21+q22q21−q22)]. If q1=−q2, then z=0.
Therefore, locus of points where potential is zero is the plane through mid point of the two charges.
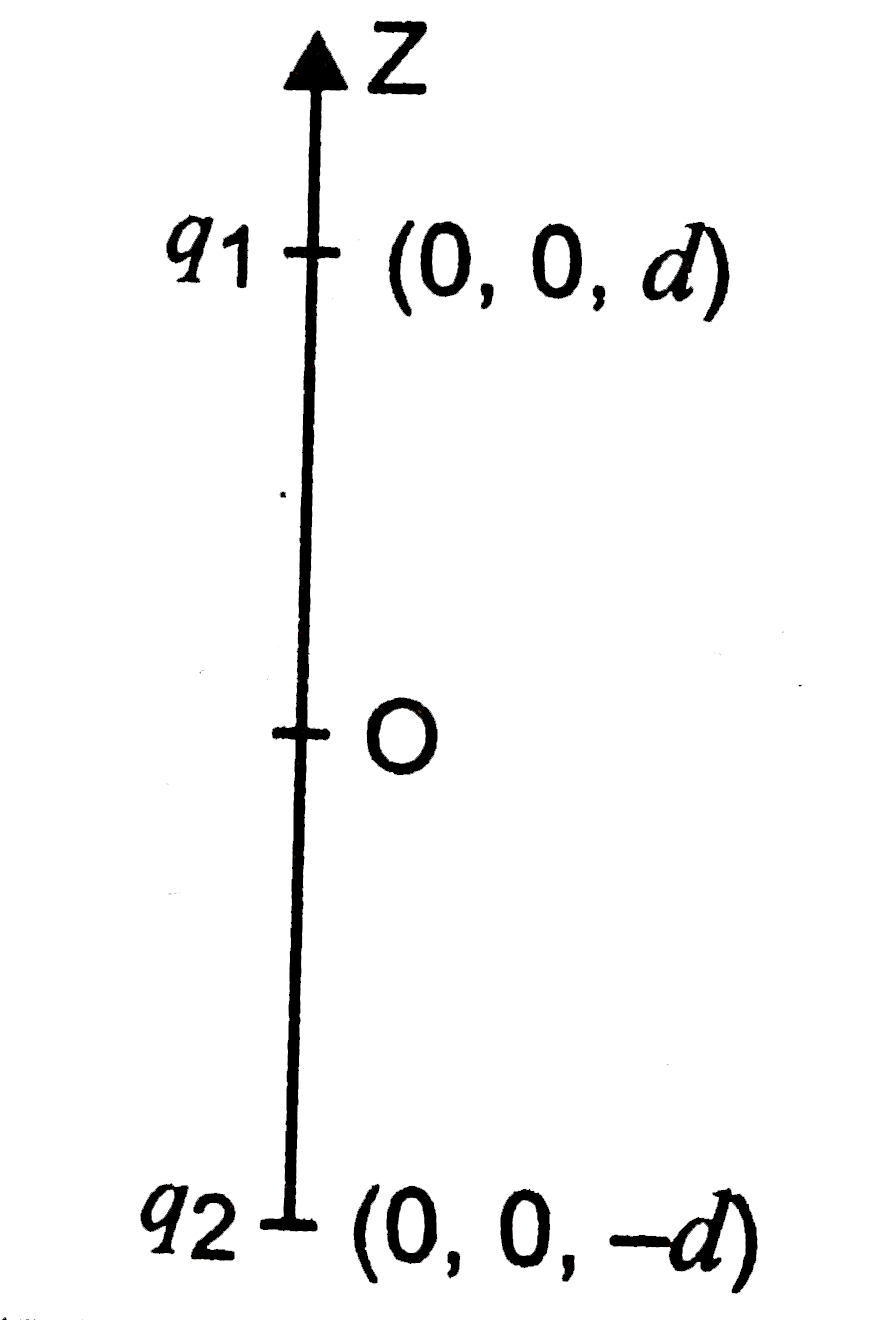
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS7videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - Exercise414videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks1videos
ELECTRONIC DEVICES
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
Similar Questions
Knowledge Check
- Question 1 - Select One
The positions of two point charges q1 and q2 are →r1 and →r2 , respectively. Find the position of the point where the net field is zero due to thses charges.
A→r1√q1+→r2√q2√q1+√q2B→r1√q2+→r2√q1√q1+√q2C→r1√q2+→r2√q1√q1+q2D→r1√q1+→r2√q2√q1+q2 - Question 2 - Select One
Three point charge q1=1μC,q2=−2μC and q3=3μC are placed at (1m,0,0),(0,2m,0) and (0,0,3m) respectively. Find the electric potential at the origin.
A2.0×103VB9.0×103VC1.0×103VD10×103V
Two point charges q and -2q are kept on x-axis at ( -a,0,0) and ( 2a,0,0) . Find the locus of all points wher electric potential is zero. Assume that electric potential at infinite distance from a point charge is zero.
View SolutionTwo point charges of magnitude +qand−q are placed at (−d/2,0,0)and(d/2,0,0) are respectively. Find the equation of the euipotential surface where the potential is zero.
View SolutionTwo charges - q and +q are located at points (0, 0, - a) and (0,0, a), respectively.
What is the electrostatic potential at the points (0, 0, z) and (x, y,0) ?View SolutionTwo charges - q and +q are located at points (0, 0, - a) and (0,0, a), respectively.
Obtain the dependence of potential on the distance r of a point from the origin when ra>>1.View SolutionThe point charges q1=1μC,q2=−2μC and q3=3μC are placed at (1m,0,0),(0,2m,0) and (0,0,3m) respectively. Find the electric potential at origin.
View SolutionTwo electric charges q1=qandq2=−2q are placed at a distance l = 6a apart. Find the locus of points in the plane of the charges where the field potential is zero
View Solution

